Lcm Of 2 And 12
seoindie
Sep 14, 2025 · 6 min read
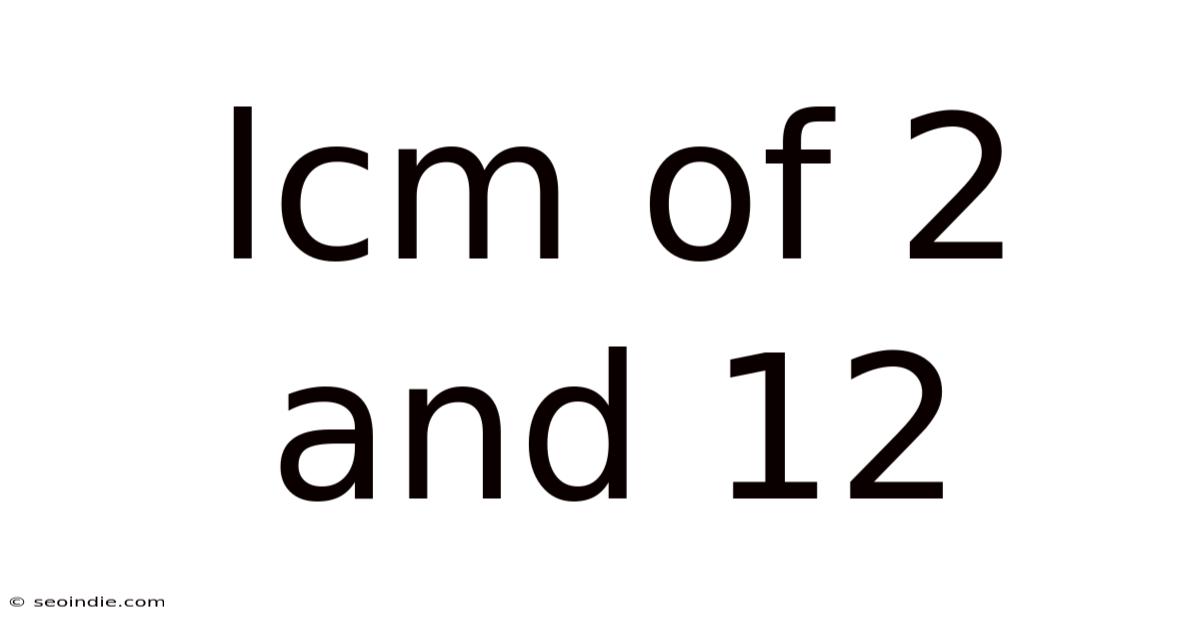
Table of Contents
Understanding the Least Common Multiple (LCM) of 2 and 12: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding its underlying principles unlocks a deeper appreciation for number theory and its applications in various fields. This comprehensive guide will delve into calculating the LCM of 2 and 12, exploring different methods and providing a solid foundation for understanding LCMs in general. We'll move beyond simply finding the answer and explore the 'why' behind the calculations, making this concept clear for learners of all levels.
Introduction to Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. Understanding LCMs is crucial in various mathematical contexts, including simplifying fractions, solving problems involving cyclical events, and even in more advanced areas like abstract algebra.
Method 1: Listing Multiples
The most straightforward method for finding the LCM of 2 and 12 is by listing the multiples of each number and identifying the smallest common multiple.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 12: 12, 24, 36, 48, 60...
By comparing the lists, we can see that the smallest number appearing in both lists is 12. Therefore, the LCM of 2 and 12 is 12. This method is intuitive and easy to understand, especially for smaller numbers. However, for larger numbers, this method can become cumbersome and inefficient.
Method 2: Prime Factorization
A more efficient and generalizable method for finding the LCM involves prime factorization. This method is particularly useful when dealing with larger numbers or multiple numbers.
-
Find the prime factorization of each number:
- 2 = 2¹
- 12 = 2² x 3¹
-
Identify the highest power of each prime factor:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
-
Multiply the highest powers together:
- LCM(2, 12) = 2² x 3¹ = 4 x 3 = 12
Therefore, the LCM of 2 and 12 using prime factorization is 12. This method is more systematic and avoids the need for extensive listing, making it suitable for larger numbers and more complex scenarios.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are closely related. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers. This relationship provides another efficient method for calculating the LCM.
-
Find the GCD of 2 and 12: The GCD is the largest number that divides both 2 and 12 without leaving a remainder. In this case, the GCD(2, 12) = 2.
-
Use the formula: LCM(a, b) = (a x b) / GCD(a, b)
- LCM(2, 12) = (2 x 12) / 2 = 12
Therefore, using the GCD method, the LCM of 2 and 12 is again 12. This method highlights the inherent connection between LCM and GCD and offers an alternative approach to calculation.
Understanding the Relationship between LCM and GCD
The relationship between LCM and GCD is fundamental in number theory. It demonstrates a beautiful symmetry in how these two concepts are intertwined. The formula:
LCM(a, b) * GCD(a, b) = a * b
holds true for any two positive integers a and b. This formula provides a powerful tool for calculating either the LCM or the GCD if the other is known. Understanding this relationship enhances your overall understanding of number theory and its applications.
Applications of LCM
The concept of LCM extends beyond simple arithmetic exercises. It finds practical application in a wide range of scenarios:
-
Scheduling: Imagine two buses arrive at a station at different intervals. One bus arrives every 2 hours, and another every 12 hours. The LCM (12 hours) helps determine when both buses will arrive at the station simultaneously.
-
Fraction Simplification: When adding or subtracting fractions, finding the LCM of the denominators is crucial for obtaining a common denominator.
-
Pattern Recognition: LCMs are useful in identifying repeating patterns and cycles in various phenomena.
-
Engineering and Design: In engineering and design, LCM is used for optimizing designs and scheduling processes that involve multiple repetitive cycles.
-
Music Theory: The LCM plays a role in understanding musical intervals and harmonies.
Why is the LCM of 2 and 12 important?
The LCM of 2 and 12 (which is 12) signifies the smallest number that is divisible by both 2 and 12. This seemingly simple concept has profound implications in various fields. For example, in scheduling, if two events occur at intervals of 2 and 12 units respectively (time, distance etc.), the LCM determines when both events will coincide. Understanding the LCM helps us predict and manage concurrent events efficiently.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers are not integers? A: The concept of LCM is primarily defined for integers. For non-integer numbers, the concept of least common multiple needs to be adapted using different mathematical frameworks.
-
Q: Can the LCM be greater than the two numbers? A: Yes, the LCM is often greater than or equal to the larger of the two numbers. It will only be equal if one number is a multiple of the other.
-
Q: Can the LCM be less than the smaller number? A: No, the LCM can never be less than the larger of the two numbers.
-
Q: What is the LCM of 0 and any other number? A: The LCM of 0 and any other number is undefined because 0 does not have a defined positive multiple.
-
Q: How do I find the LCM of more than two numbers? A: You can extend the prime factorization method or the GCD method to handle multiple numbers. For prime factorization, you consider all the prime factors and their highest powers. For the GCD method, you would iteratively find the GCD of pairs and apply the formula repeatedly.
Conclusion: Mastering the LCM
Understanding the least common multiple (LCM) is a fundamental skill in mathematics with practical applications in diverse fields. This guide has explored several methods for calculating the LCM, emphasizing both the procedural aspects and the conceptual underpinnings. The relationship between LCM and GCD adds another layer of understanding, highlighting the interconnectedness of mathematical concepts. By mastering the LCM, you not only enhance your arithmetic skills but also develop a deeper appreciation for the elegance and practicality of number theory. Remember, the key is not just to find the answer (in this case, 12), but to grasp the underlying principles and their implications. This understanding empowers you to approach more complex problems with confidence and clarity.
Latest Posts
Latest Posts
-
The Ugly Duckling Short Story
Sep 14, 2025
-
Words To Describe My Father
Sep 14, 2025
-
Is Bacteria Abiotic Or Biotic
Sep 14, 2025
-
How Much Is 35 Cm
Sep 14, 2025
-
Indigo Vs Violet Vs Purple
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.