Lcm Of 2 3 6
seoindie
Sep 16, 2025 · 7 min read
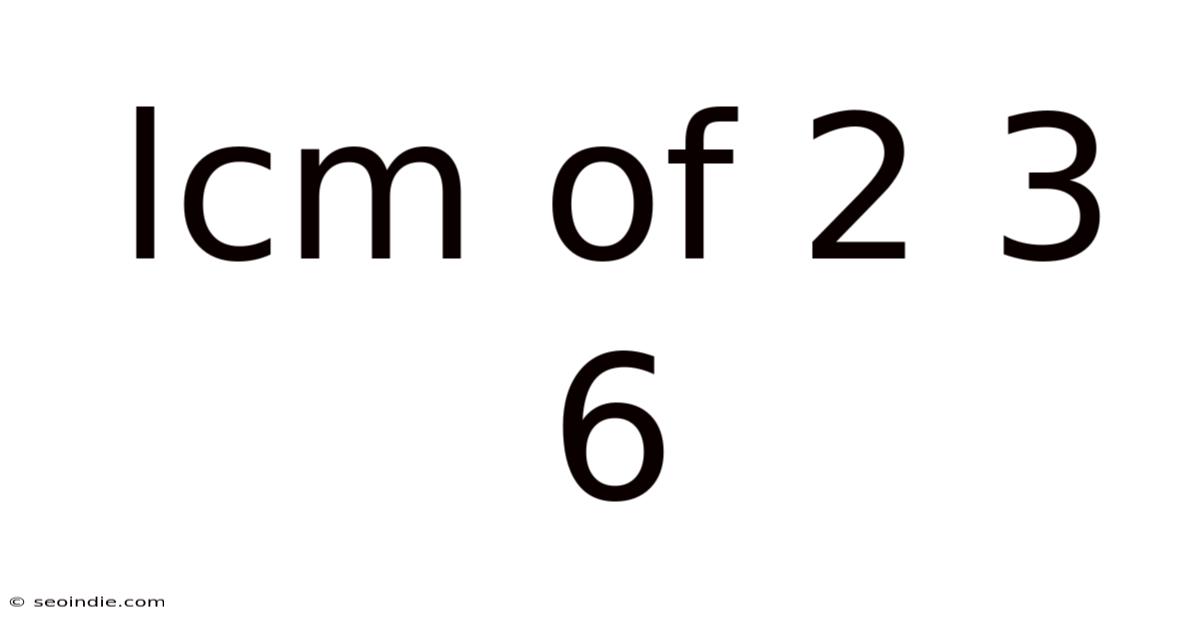
Table of Contents
Understanding the Least Common Multiple (LCM): A Deep Dive into the LCM of 2, 3, and 6
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex problems in algebra and beyond. This article provides a comprehensive guide to understanding LCM, focusing specifically on finding the LCM of 2, 3, and 6. We'll explore different methods, delve into the underlying mathematical principles, and address frequently asked questions. By the end, you'll not only know the LCM of 2, 3, and 6 but also possess a strong foundation in calculating LCMs for any set of numbers.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be evenly divided by all the numbers in the set. For instance, multiples of 2 are 2, 4, 6, 8, 10... Multiples of 3 are 3, 6, 9, 12... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Understanding LCM is vital for various mathematical operations, including:
- Simplifying fractions: Finding the LCM of the denominators allows you to add or subtract fractions efficiently.
- Solving equations: LCM is crucial in solving equations involving fractions and rational expressions.
- Real-world applications: LCM finds applications in scheduling problems, determining cyclical patterns, and other areas where finding common multiples is necessary.
Methods for Finding the LCM
Several methods can be used to find the LCM of a set of numbers. Let's explore the most common ones, focusing on how to find the LCM of 2, 3, and 6.
1. Listing Multiples Method:
This method involves listing the multiples of each number until you find the smallest common multiple.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24...
- Multiples of 6: 6, 12, 18, 24, 30...
By inspecting the lists, we can see that the smallest number that appears in all three lists is 6. Therefore, the LCM(2, 3, 6) = 6. This method works well for smaller numbers, but it can become cumbersome for larger numbers.
2. Prime Factorization Method:
This is a more efficient method, especially for larger numbers. It involves breaking down each number into its prime factors.
- Prime factorization of 2: 2
- Prime factorization of 3: 3
- Prime factorization of 6: 2 x 3
To find the LCM using prime factorization:
- Identify all the prime factors present in the numbers. In this case, we have 2 and 3.
- For each prime factor, take the highest power present in any of the factorizations. Here, the highest power of 2 is 2¹ and the highest power of 3 is 3¹.
- Multiply these highest powers together. LCM(2, 3, 6) = 2¹ x 3¹ = 6.
This method is more systematic and efficient than listing multiples, especially when dealing with larger numbers or a greater number of integers.
3. Greatest Common Divisor (GCD) Method:
The LCM and GCD (Greatest Common Divisor) of a set of numbers are related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. While less direct for finding the LCM of multiple numbers, it's useful to illustrate the connection.
Let's find the GCD of 2 and 3. The only common divisor of 2 and 3 is 1. Therefore, GCD(2, 3) = 1. However, this method becomes less practical with three or more numbers, as the relationship doesn't extend directly to more than two numbers. For our example, using this would involve finding the GCD of pairs (e.g., GCD(2,3), GCD(2,6), GCD(3,6)) then constructing a relationship, which is less efficient than prime factorization.
Applying the LCM: Real-World Examples
The concept of LCM has practical applications in various real-world scenarios. Here are a few examples:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 2 hours, and the other every 3 hours. To determine when both buses will arrive simultaneously, you would find the LCM of 2 and 3, which is 6. Therefore, both buses will arrive together every 6 hours.
-
Task Repetition: Suppose you have two tasks: one that repeats every 2 days and another that repeats every 6 days. To find when both tasks will coincide, calculate the LCM(2, 6) = 6. Both tasks will occur together every 6 days.
-
Fractions: When adding or subtracting fractions, you must find a common denominator, which is the LCM of the denominators. For instance, to add 1/2 and 1/3, you would find the LCM of 2 and 3 (which is 6), and then rewrite the fractions with a denominator of 6: (3/6) + (2/6) = 5/6.
The Significance of the LCM of 2, 3, and 6
In the specific case of the numbers 2, 3, and 6, the LCM is relatively straightforward to calculate using any of the methods. However, understanding the process is crucial for tackling more complex LCM problems. The fact that the LCM of 2, 3, and 6 is 6 highlights the concept that if one number is a multiple of another number within a set, the LCM will be the larger number. In this case, 6 is a multiple of both 2 and 3. This shortcut can be beneficial in solving some LCM problems more quickly.
Mathematical Explanation and Underlying Principles
The prime factorization method provides a deeper understanding of the mathematical principles behind LCM. Every integer can be uniquely expressed as a product of prime numbers (Fundamental Theorem of Arithmetic). This unique factorization allows us to systematically find the LCM by identifying the highest power of each prime factor present in the numbers.
By understanding prime factorization, we can extend the concept of LCM to more complex scenarios involving larger numbers and a larger number of integers. The process remains consistent; we break down each number into its prime factors and then construct the LCM using the highest powers of each prime factor.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
A1: The LCM (Least Common Multiple) is the smallest number that is a multiple of all the given numbers. The GCD (Greatest Common Divisor) is the largest number that divides all the given numbers without leaving a remainder. They are inversely related; the product of the LCM and GCD of two numbers equals the product of the two numbers.
Q2: Can the LCM of a set of numbers be larger than the largest number in the set?
A2: Yes, absolutely. This happens when there are no common factors among the numbers, besides 1. For example, the LCM of 5 and 7 is 35, which is greater than both 5 and 7.
Q3: How do I find the LCM of more than three numbers?
A3: The same methods apply. For the prime factorization method, you simply extend the process to include all the numbers in the set. List all prime factors, find the highest power of each, and multiply them together. The listing multiples method becomes increasingly impractical with more numbers.
Q4: What if one of the numbers is zero?
A4: The LCM is undefined if one of the numbers is 0. This is because zero is a multiple of every number, and there is no smallest multiple of zero.
Q5: Are there any online calculators or tools to find the LCM?
A5: Yes, numerous online calculators are available to compute the LCM of any set of numbers quickly and easily. These tools can be beneficial for checking your work or handling large sets of numbers. However, understanding the underlying principles remains crucial for developing a strong mathematical foundation.
Conclusion
Finding the LCM, particularly the LCM of 2, 3, and 6, is an important skill in mathematics. This article has explored various methods, delved into the underlying mathematical principles, and addressed frequently asked questions. By understanding the concepts of LCM, prime factorization, and GCD, you can confidently calculate the LCM of any set of numbers and apply this knowledge to various real-world problems. Remember, the key is to practice and understand the methods; the more you practice, the more proficient you will become. Don't hesitate to revisit this article or explore additional resources to strengthen your understanding further.
Latest Posts
Latest Posts
-
Words With Y And Q
Sep 16, 2025
-
Physical Mapping Vs Genetic Mapping
Sep 16, 2025
-
3 8 Into A Percent
Sep 16, 2025
-
1990 In Roman Numerals Tattoo
Sep 16, 2025
-
Net Investment Vs Gross Investment
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 3 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.