Lcm Of 18 And 42
seoindie
Sep 13, 2025 · 6 min read
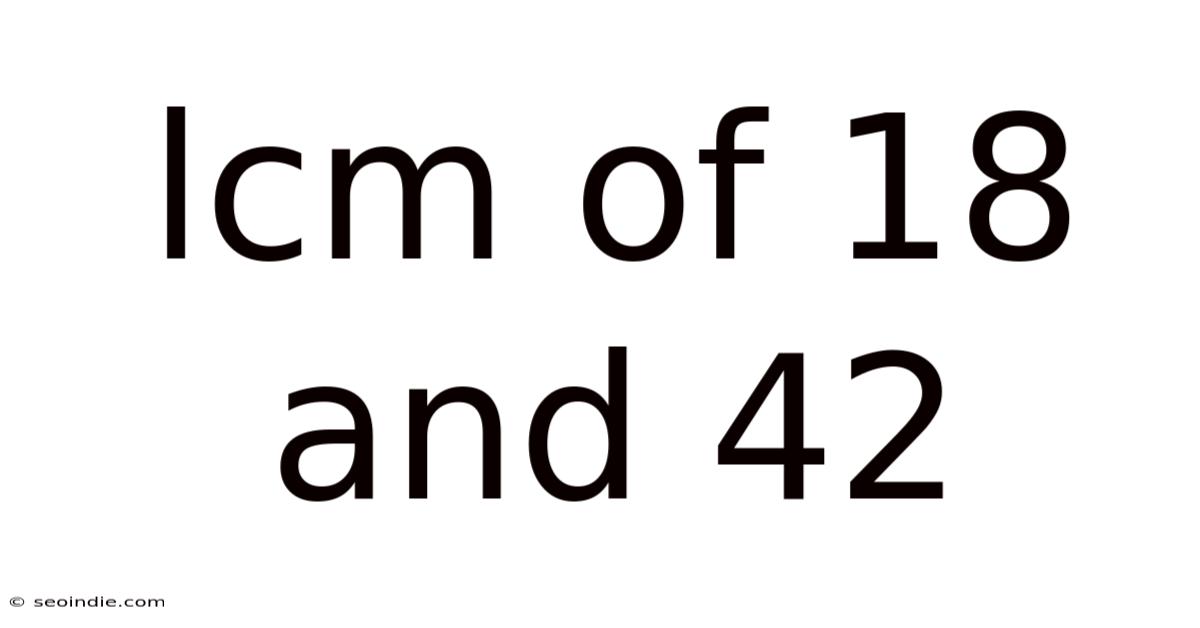
Table of Contents
Finding the Least Common Multiple (LCM) of 18 and 42: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating the LCM opens doors to a deeper appreciation of number theory. This article will explore various ways to determine the LCM of 18 and 42, providing a detailed explanation suitable for learners of all levels. We will delve into the definition of LCM, explore different calculation methods, and touch upon its applications in various mathematical contexts. By the end, you'll not only know the LCM of 18 and 42 but also possess a robust understanding of this fundamental concept.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 18 and 42, let's define what it means. The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both numbers divide into evenly. Understanding this definition is crucial for grasping the significance of LCM in various mathematical applications.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers like 18 and 42, is listing the multiples of each number until you find the smallest common multiple.
- Multiples of 18: 18, 36, 54, 72, 90, 108, 126, 144, 162, 180, 198, 216, 234, 252…
- Multiples of 42: 42, 84, 126, 168, 210, 252…
Notice that 126 appears in both lists. However, to be sure it's the least common multiple, we continue listing until we find a common multiple. We see that 126 is the smallest number present in both lists. Therefore, the LCM of 18 and 42 is 126. This method is simple for small numbers but becomes less efficient for larger numbers.
Method 2: Prime Factorization
A more efficient and systematic method, especially for larger numbers, involves finding the prime factorization of each number. The prime factorization of a number is expressing it as a product of its prime factors.
- Prime factorization of 18: 2 × 3 × 3 = 2 × 3²
- Prime factorization of 42: 2 × 3 × 7
Now, to find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together.
- Highest power of 2: 2¹
- Highest power of 3: 3²
- Highest power of 7: 7¹
LCM(18, 42) = 2¹ × 3² × 7¹ = 2 × 9 × 7 = 126
This method is significantly more efficient for larger numbers as it avoids the tedious process of listing multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both numbers evenly. We can use the relationship between LCM and GCD to calculate the LCM:
LCM(a, b) = (|a × b|) / GCD(a, b)
First, let's find the GCD of 18 and 42 using the Euclidean algorithm:
- Divide 42 by 18: 42 = 2 × 18 + 6
- Divide 18 by the remainder 6: 18 = 3 × 6 + 0
The last non-zero remainder is the GCD, which is 6.
Now, we can calculate the LCM:
LCM(18, 42) = (18 × 42) / GCD(18, 42) = (756) / 6 = 126
This method is particularly useful when dealing with larger numbers where prime factorization might become cumbersome. The Euclidean algorithm provides a more efficient way to find the GCD.
Explanation of the Methods: A Deeper Dive
Let's analyze why these methods work. The listing multiples method is based on the very definition of LCM – finding the smallest common multiple. However, it's not scalable for larger numbers.
The prime factorization method works because it ensures that we include all the prime factors needed to make both numbers multiples. By taking the highest power of each prime factor, we guarantee that the resulting number is divisible by both original numbers. This is a powerful and efficient technique.
The GCD method leverages the fundamental relationship between LCM and GCD. The product of two numbers is always equal to the product of their LCM and GCD. This relationship is a cornerstone of number theory and provides an alternative, often more efficient, way to calculate the LCM.
Applications of LCM
The concept of LCM has wide-ranging applications in various mathematical and real-world scenarios:
- Fractions: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Scheduling: Determining when events with different repeating cycles will occur simultaneously (e.g., two buses arriving at the same stop at the same time).
- Gear ratios: In mechanics, gear ratios and synchronized rotations often involve LCM calculations.
- Music theory: Determining the least common multiple of note durations helps in understanding musical rhythms and harmonies.
- Modular arithmetic: LCM plays a critical role in solving congruences and other problems in modular arithmetic.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest number that is a multiple of both given numbers, while the GCD (Greatest Common Divisor) is the largest number that divides both given numbers without leaving a remainder.
Q: Can the LCM of two numbers be smaller than either number?
A: No, the LCM of two numbers is always greater than or equal to the larger of the two numbers.
Q: Is there a formula to calculate the LCM directly without using the GCD?
A: While there isn't a single, direct formula without involving prime factorization or a related concept like GCD, the prime factorization method directly calculates the LCM without explicitly calculating the GCD first.
Q: How can I use a calculator to find the LCM?
A: Many scientific calculators have a built-in function to calculate the LCM of two or more numbers. Check your calculator's manual for instructions. Online calculators are also readily available.
Q: What if I have more than two numbers? How do I find the LCM?
A: You can extend the prime factorization method or the GCD method to find the LCM of more than two numbers. For prime factorization, you consider the highest power of each prime factor present in any of the numbers. For the GCD method, you would need to iteratively find the GCD of pairs of numbers and use the relationship to find the LCM of all numbers.
Conclusion
Finding the least common multiple of 18 and 42, as demonstrated above, highlights the power and versatility of different mathematical techniques. While the method of listing multiples is simple for small numbers, the prime factorization method and the GCD method provide efficient and systematic approaches for handling larger numbers. Understanding these methods not only allows you to solve specific problems but also cultivates a deeper understanding of fundamental number theory concepts applicable in various fields. Remember to choose the method best suited to your needs and the complexity of the numbers involved. The LCM, along with its counterpart, the GCD, are essential tools in the mathematician's toolbox, enabling efficient problem-solving across diverse mathematical domains.
Latest Posts
Latest Posts
-
Polar To Rectangular Conversion Calculator
Sep 14, 2025
-
Adding And Subtracting Rationals Calculator
Sep 14, 2025
-
What Is Fax Short For
Sep 14, 2025
-
How Do You Spell 71
Sep 14, 2025
-
Boiling Point Glacial Acetic Acid
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 18 And 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.