Lcm Of 15 And 6
seoindie
Sep 13, 2025 · 5 min read
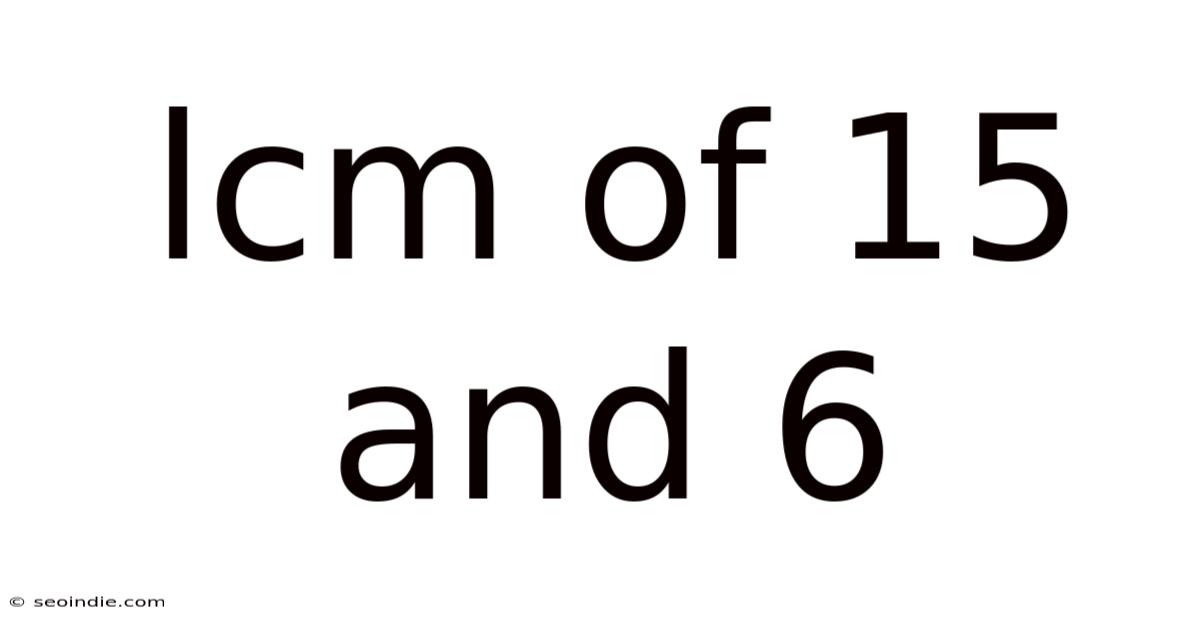
Table of Contents
Finding the LCM of 15 and 6: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in arithmetic with applications extending into algebra, calculus, and beyond. This article will provide a thorough exploration of how to find the LCM of 15 and 6, illustrating multiple methods and explaining the underlying mathematical principles. We'll cover various techniques suitable for different skill levels, from elementary school students to those refreshing their mathematical understanding. By the end, you'll not only know the LCM of 15 and 6 but also understand how to calculate the LCM of any two numbers.
Understanding Least Common Multiple (LCM)
Before diving into the calculation, let's clarify what the least common multiple actually is. The LCM of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder. Understanding this definition is key to grasping the various methods we'll explore.
Method 1: Listing Multiples
The most straightforward method, particularly useful for smaller numbers like 15 and 6, involves listing the multiples of each number until a common multiple is found.
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66...
By comparing the lists, we see that the smallest number appearing in both lists is 30. Therefore, the LCM of 15 and 6 is 30. This method is simple but can become cumbersome for larger numbers.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the mathematical principles involved. It relies on expressing each number as a product of its prime factors.
Step 1: Find the prime factorization of each number.
- 15: The prime factorization of 15 is 3 x 5.
- 6: The prime factorization of 6 is 2 x 3.
Step 2: Identify the highest power of each prime factor present in either factorization.
In our example, the prime factors are 2, 3, and 5.
- The highest power of 2 is 2¹ (from the factorization of 6).
- The highest power of 3 is 3¹ (present in both factorizations).
- The highest power of 5 is 5¹ (from the factorization of 15).
Step 3: Multiply the highest powers together.
2¹ x 3¹ x 5¹ = 2 x 3 x 5 = 30
Therefore, the LCM of 15 and 6 is 30. This method is more systematic and works effectively even for large numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of two numbers are related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship provides an alternative method for finding the LCM.
Step 1: Find the GCD of 15 and 6.
The GCD is the largest number that divides both 15 and 6 without leaving a remainder. We can find the GCD using the Euclidean algorithm or by listing the divisors.
- Divisors of 15: 1, 3, 5, 15
- Divisors of 6: 1, 2, 3, 6
The largest common divisor is 3. Therefore, the GCD(15, 6) = 3.
Step 2: Use the formula: LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers. Substituting the values:
LCM(15, 6) x 3 = 15 x 6
LCM(15, 6) = (15 x 6) / 3 = 90 / 3 = 30
Therefore, the LCM of 15 and 6 is 30. This method is particularly useful when the GCD is easily determined.
Visualizing LCM with Venn Diagrams
While not a direct calculation method, Venn diagrams offer a visual representation of the concept, enhancing understanding. For our example:
Draw two overlapping circles, one representing the factors of 15 (3 and 5) and the other representing the factors of 6 (2 and 3). The overlapping section contains the common factor (3). To find the LCM, we multiply all the unique factors, including the common factor only once: 2 x 3 x 5 = 30.
Applications of LCM in Real-World Scenarios
The LCM finds practical applications in various scenarios:
- Scheduling: Imagine two buses departing from the same station at different intervals. The LCM helps determine when they will depart simultaneously again.
- Fractions: Finding the LCM of the denominators is crucial when adding or subtracting fractions. This ensures a common denominator, simplifying the calculation.
- Pattern Recognition: Identifying repeating patterns often involves finding the LCM of the lengths of individual cycles.
- Measurement Conversions: Converting between units of measurement may sometimes require the use of LCM.
These examples highlight the widespread applicability of LCM, demonstrating its significance beyond purely mathematical contexts.
Frequently Asked Questions (FAQ)
-
Q: What if I have more than two numbers? A: The methods discussed, particularly prime factorization, can be extended to find the LCM of more than two numbers. You simply find the prime factorization of each number and then identify the highest power of each prime factor present.
-
Q: Is there a formula for LCM? A: There isn't a single, concise formula for LCM, but the relationship between LCM and GCD (LCM(a, b) x GCD(a, b) = a x b) is a crucial formula.
-
Q: What if the two numbers are the same? A: If the two numbers are identical, their LCM is simply the number itself. For example, LCM(15,15) = 15.
-
Q: Can the LCM ever be larger than the product of the two numbers? A: No, the LCM will always be less than or equal to the product of the two numbers.
Conclusion
Determining the least common multiple is a fundamental skill in mathematics. We have explored various methods for finding the LCM of 15 and 6, each offering a different perspective and level of complexity. From the simple method of listing multiples to the more efficient prime factorization and GCD-based approaches, choosing the appropriate method depends on the context and the size of the numbers involved. Understanding these methods provides a solid foundation for tackling more complex mathematical problems. The LCM’s practical applications across diverse fields underscore its importance beyond the classroom, making it a crucial concept to master. Remember, practice is key; the more you work with these methods, the more intuitive and efficient your calculations will become.
Latest Posts
Latest Posts
-
What Is A Compound Microscope
Sep 13, 2025
-
10 000 M2 In Acres
Sep 13, 2025
-
3 Classes Of Levers Examples
Sep 13, 2025
-
Words With U And E
Sep 13, 2025
-
Aerobic Respiration Takes Place In
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 15 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.