Lcm Of 15 And 10
seoindie
Sep 13, 2025 · 5 min read
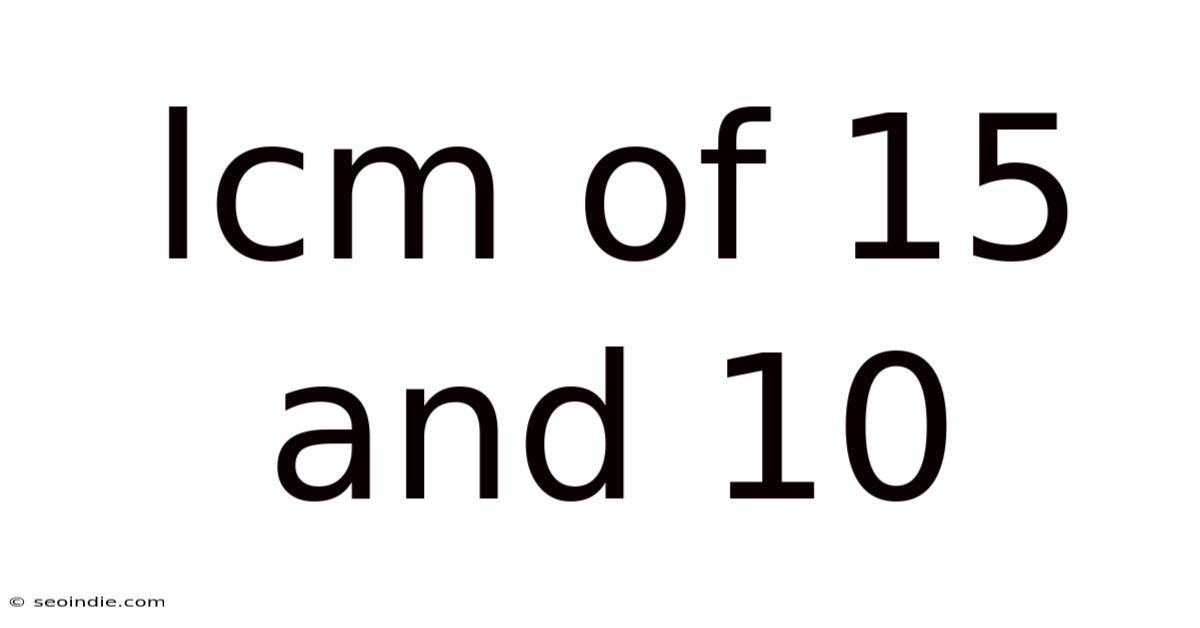
Table of Contents
Unveiling the Least Common Multiple (LCM) of 15 and 10: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a world of mathematical possibilities. This comprehensive guide delves into the LCM of 15 and 10, explaining various methods to calculate it, exploring its significance in different mathematical contexts, and addressing frequently asked questions. We'll go beyond a simple answer, providing a foundational understanding of LCM and its applications.
Understanding Least Common Multiple (LCM)
Before we tackle the LCM of 15 and 10 specifically, let's establish a solid understanding of what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers in question as factors.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... and multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Calculating the LCM of 15 and 10: Three Proven Methods
Now, let's focus on finding the LCM of 15 and 10. We'll explore three common methods:
1. Listing Multiples Method
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 10: 10, 20, 30, 40, 50...
- Multiples of 15: 15, 30, 45, 60...
The smallest number that appears in both lists is 30. Therefore, the LCM of 15 and 10 is 30. This method works well for smaller numbers but can become cumbersome with larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves breaking down each number into its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
- Prime factorization of 10: 2 x 5
- Prime factorization of 15: 3 x 5
To find the LCM, we take the highest power of each prime factor present in the factorizations and multiply them together. In this case:
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Therefore, LCM(15, 10) = 2 x 3 x 5 = 30
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD). The GCD is the largest number that divides both numbers without leaving a remainder. There's a useful formula connecting LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
First, let's find the GCD of 15 and 10 using the Euclidean algorithm:
- Divide the larger number (15) by the smaller number (10): 15 ÷ 10 = 1 with a remainder of 5.
- Replace the larger number with the smaller number (10) and the smaller number with the remainder (5): 10 ÷ 5 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 5.
Now, we can use the formula:
LCM(15, 10) x GCD(15, 10) = 15 x 10 LCM(15, 10) x 5 = 150 LCM(15, 10) = 150 ÷ 5 = 30
The Significance of LCM in Real-World Applications
The concept of LCM extends far beyond simple arithmetic exercises. It finds practical applications in various fields:
-
Scheduling: Imagine two buses departing from the same station at different intervals. One bus leaves every 10 minutes, and the other leaves every 15 minutes. The LCM (30 minutes) determines when both buses will depart simultaneously again.
-
Fractions: Finding a common denominator when adding or subtracting fractions involves determining the LCM of the denominators. This ensures accurate calculations.
-
Cyclic Processes: In engineering and physics, understanding cyclical processes often requires determining when events will coincide. The LCM helps pinpoint these coincidences.
-
Music Theory: The LCM plays a role in understanding musical intervals and harmonies. It helps determine when different musical phrases will align rhythmically.
Beyond the Basics: Extending the Concept of LCM
The LCM concept easily expands to include more than two numbers. For instance, to find the LCM of 10, 15, and 20, we can use the prime factorization method:
- 10 = 2 x 5
- 15 = 3 x 5
- 20 = 2² x 5
The highest powers are 2², 3¹, and 5¹. Therefore, LCM(10, 15, 20) = 2² x 3 x 5 = 60
Frequently Asked Questions (FAQ)
Q: What if the two numbers are relatively prime?
A: If two numbers are relatively prime (meaning their GCD is 1), their LCM is simply their product. For example, the LCM of 7 and 12 is 84 (7 x 12).
Q: Can the LCM be larger than the product of the two numbers?
A: No, the LCM of two numbers is always less than or equal to the product of the two numbers.
Q: Are there any shortcuts for finding the LCM of large numbers?
A: While the prime factorization method remains efficient, computational tools and algorithms can significantly speed up the process for very large numbers.
Q: How does LCM relate to GCD?
A: The LCM and GCD of two numbers are inversely related. As the GCD increases, the LCM decreases, and vice versa. Their product always equals the product of the two original numbers.
Conclusion
Finding the LCM of 15 and 10, though seemingly simple, provides a gateway to understanding a crucial concept in mathematics. This exploration has revealed three distinct methods for calculating the LCM, highlighting the efficiency of prime factorization. Beyond its fundamental arithmetic applications, the LCM proves indispensable in diverse fields, from scheduling and fractions to music theory and engineering. By grasping the underlying principles and various calculation methods, we can confidently approach more complex LCM problems and appreciate the breadth of its real-world significance. The LCM is not just a mathematical concept; it's a practical tool that helps us understand and solve problems in various aspects of life.
Latest Posts
Latest Posts
-
500 M2 To Square Feet
Sep 14, 2025
-
Letter Of Consent Sample Format
Sep 14, 2025
-
Thirty Six In Roman Numerals
Sep 14, 2025
-
Add Subtract Multiply Divide Keywords
Sep 14, 2025
-
12 Feet In A Yard
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 15 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.