Lcm Of 14 And 49
seoindie
Sep 13, 2025 · 5 min read
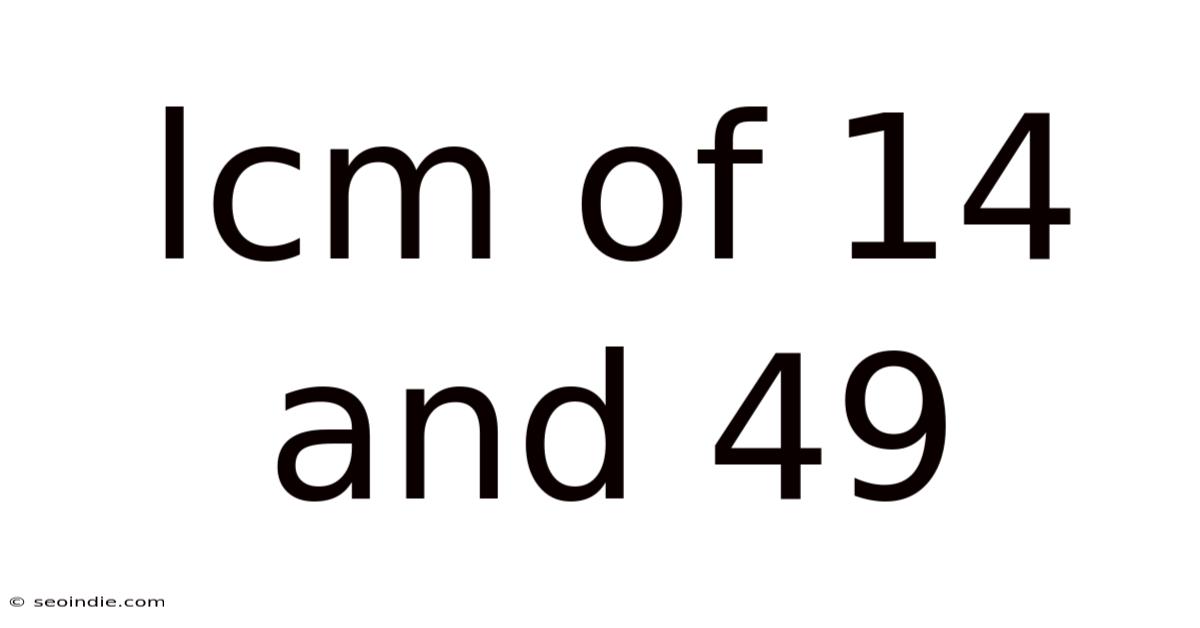
Table of Contents
Unveiling the Least Common Multiple (LCM) of 14 and 49: A Deep Dive into Number Theory
Finding the Least Common Multiple (LCM) might seem like a simple arithmetic task, especially with smaller numbers like 14 and 49. However, understanding the underlying principles and different methods for calculating the LCM opens a door to a fascinating world of number theory and its practical applications. This comprehensive guide will not only show you how to find the LCM of 14 and 49 but will also explore the theoretical foundations and various approaches, ensuring a thorough understanding of this fundamental concept.
Understanding Least Common Multiple (LCM)
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the given integers. Think of it as the smallest number that contains all the given numbers as factors. This concept is crucial in various mathematical applications, from solving fraction problems to scheduling events with recurring intervals.
For instance, if you have two gears with 14 and 49 teeth, respectively, the LCM will represent the number of rotations after which both gears will simultaneously return to their starting positions. This seemingly simple example demonstrates the practical relevance of the LCM in diverse fields.
Method 1: Prime Factorization
This method is considered a cornerstone approach for calculating the LCM, especially when dealing with larger numbers or a set of numbers. It leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers (primes are numbers divisible only by 1 and themselves).
Steps:
-
Find the prime factorization of each number:
- 14 = 2 x 7
- 49 = 7 x 7 = 7²
-
Identify the highest power of each prime factor present in the factorizations:
- The prime factors are 2 and 7.
- The highest power of 2 is 2¹ (from the factorization of 14).
- The highest power of 7 is 7² (from the factorization of 49).
-
Multiply the highest powers of all prime factors together:
- LCM(14, 49) = 2¹ x 7² = 2 x 49 = 98
Therefore, the LCM of 14 and 49 is 98. This method provides a systematic and robust approach, applicable to any number of integers.
Method 2: Listing Multiples
This method is more intuitive and suitable for smaller numbers. It involves listing the multiples of each number until a common multiple is found. The smallest common multiple is the LCM.
Steps:
-
List the multiples of 14: 14, 28, 42, 56, 70, 84, 98, 112, ...
-
List the multiples of 49: 49, 98, 147, ...
-
Identify the smallest common multiple: The smallest number that appears in both lists is 98.
Therefore, the LCM of 14 and 49 is 98. This method is simple to visualize, but it can become less efficient with larger numbers.
Method 3: Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the Greatest Common Divisor (GCD) of two numbers. The GCD is the largest positive integer that divides both numbers without leaving a remainder. The relationship between LCM and GCD is given by the formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
where 'a' and 'b' are the two integers.
Steps:
-
Find the GCD of 14 and 49:
- We can use the Euclidean algorithm to find the GCD.
- 49 = 3 x 14 + 7
- 14 = 2 x 7 + 0
- The GCD is 7.
-
Apply the formula:
- LCM(14, 49) = (14 x 49) / 7 = 686 / 7 = 98
Therefore, the LCM of 14 and 49 is 98. This method is efficient, particularly for larger numbers where prime factorization might be more tedious.
Understanding the Euclidean Algorithm
The Euclidean algorithm, used in the GCD method, is a highly efficient method for finding the greatest common divisor of two integers. It's based on the principle that the GCD of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the remainder becomes zero. The last non-zero remainder is the GCD. Its elegance and efficiency make it a cornerstone algorithm in number theory and computer science.
Applications of LCM
The LCM has far-reaching applications across various disciplines:
-
Fractions: Finding the LCM of the denominators is crucial when adding or subtracting fractions. It allows us to find a common denominator, simplifying the calculation.
-
Scheduling: Determining the time when two or more events with periodic intervals will occur simultaneously. For instance, if two buses arrive at a station every 14 and 49 minutes, respectively, the LCM (98 minutes) indicates when they will arrive together.
-
Modular Arithmetic: LCM plays a vital role in solving problems related to congruences and modular arithmetic, fundamental in cryptography and computer science.
-
Music Theory: LCM helps determine the least common denominator for musical intervals and rhythms.
-
Engineering: LCM finds applications in gear ratios, synchronized processes, and other engineering tasks requiring periodic synchronization.
Frequently Asked Questions (FAQ)
-
What if I have more than two numbers? The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, you consider the highest power of each prime factor from all the numbers. For the GCD method, you would iteratively find the LCM of pairs of numbers.
-
Is there a unique LCM for any set of numbers? Yes, for any given set of integers (excluding zero), there is always a unique least common multiple.
-
What is the LCM of 0 and any other number? The LCM of 0 and any other number is undefined because 0 is a multiple of every number.
-
How can I verify my LCM calculation? You can verify your result by checking if the calculated LCM is divisible by all the given numbers.
Conclusion
Finding the LCM of 14 and 49, while seemingly straightforward, provides a gateway to understanding fundamental concepts in number theory. The different methods presented—prime factorization, listing multiples, and the GCD method—each offer unique perspectives and efficiencies. Mastering these techniques empowers you not only to solve LCM problems effectively but also to appreciate the broader mathematical principles that underpin them. The practical applications of LCM extend far beyond simple arithmetic, highlighting its importance across various disciplines and showcasing the elegance and power of number theory. Remember, understanding the why behind the calculation is as important as knowing how to perform it. This deeper understanding will greatly enhance your mathematical skills and problem-solving abilities.
Latest Posts
Latest Posts
-
Highest Mountain Range On Earth
Sep 13, 2025
-
How Many Inches Is 148cm
Sep 13, 2025
-
What Times What Makes 72
Sep 13, 2025
-
Difference Between Actin And Myosin
Sep 13, 2025
-
How Much Is 100 000
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 14 And 49 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.