Lcm Of 14 And 35
seoindie
Sep 11, 2025 · 6 min read
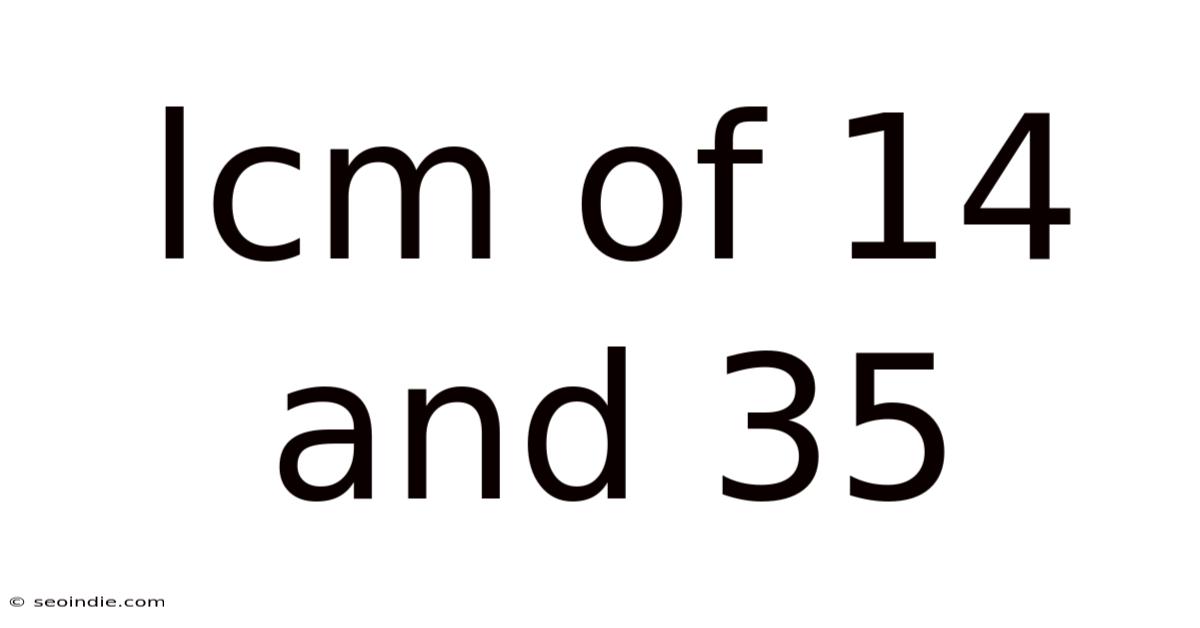
Table of Contents
Unveiling the Least Common Multiple (LCM) of 14 and 35: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles unlocks a deeper appreciation for number theory and its applications in various fields. This comprehensive guide will not only show you how to calculate the LCM of 14 and 35 but also delve into the various methods, explain the theoretical foundation, and explore the broader significance of LCMs in mathematics and beyond. We'll cover everything from basic methods suitable for beginners to more advanced techniques, ensuring a thorough understanding for learners of all levels.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the integers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer that is divisible by both 2 and 3. Understanding LCMs is crucial in various mathematical operations, from simplifying fractions to solving problems involving rhythmic patterns and cyclical events. In this article, we will focus on finding the LCM of 14 and 35, illustrating several approaches along the way.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers like 14 and 35, involves listing the multiples of each number until you find the smallest common multiple.
- Multiples of 14: 14, 28, 42, 56, 70, 84, 98, 112, 126, 140...
- Multiples of 35: 35, 70, 105, 140, 175...
By comparing the lists, we see that the smallest number appearing in both lists is 70. Therefore, the LCM of 14 and 35 is 70.
This method is simple and intuitive, but it becomes less efficient as the numbers get larger. Imagine trying to find the LCM of 147 and 231 using this method!
Method 2: Prime Factorization
This method is more efficient and works well for larger numbers. It involves expressing each number as a product of its prime factors. Prime factorization is the process of breaking down a number into its prime number components. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
- Prime factorization of 14: 2 x 7
- Prime factorization of 35: 5 x 7
To find the LCM using prime factorization, we identify the highest power of each prime factor present in either factorization.
- The prime factors present are 2, 5, and 7.
- The highest power of 2 is 2¹ = 2.
- The highest power of 5 is 5¹ = 5.
- The highest power of 7 is 7¹ = 7.
Therefore, the LCM of 14 and 35 is 2 x 5 x 7 = 70. This method is significantly more efficient than listing multiples, especially when dealing with larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are closely related. The GCD is the largest positive integer that divides both numbers without leaving a remainder. There's a handy formula connecting the LCM and GCD:
LCM(a, b) = (a x b) / GCD(a, b)
Let's find the GCD of 14 and 35 first. We can use the Euclidean algorithm for this:
- Divide the larger number (35) by the smaller number (14): 35 ÷ 14 = 2 with a remainder of 7.
- Replace the larger number with the smaller number (14) and the smaller number with the remainder (7): 14 ÷ 7 = 2 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 7.
Now, we can use the formula:
LCM(14, 35) = (14 x 35) / GCD(14, 35) = (14 x 35) / 7 = 70
This method is particularly useful when dealing with larger numbers, as finding the GCD is often easier than directly finding the LCM through other methods.
The Mathematical Foundation: Why These Methods Work
The success of these methods stems from the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. This unique factorization allows us to systematically analyze the prime components of numbers and efficiently determine their LCM and GCD. The formula relating LCM and GCD arises directly from this fundamental theorem and provides an elegant and efficient computational pathway.
LCM in Real-World Applications
The concept of LCM extends far beyond the realm of abstract mathematics. It finds practical applications in numerous fields:
- Scheduling: Imagine two buses arriving at a bus stop at different intervals. The LCM helps determine when both buses will arrive at the stop simultaneously.
- Rhythmic Patterns: In music, LCMs are used to determine when different rhythmic patterns will align.
- Gear Ratios: In mechanics, understanding LCM helps in designing gear systems with efficient synchronization.
- Cyclic Events: Predicting when certain cyclical events will coincide (e.g., planetary alignments, biological cycles) often relies on LCM calculations.
Frequently Asked Questions (FAQ)
Q1: What if the numbers have no common factors other than 1?
A1: If the GCD of two numbers is 1 (they are relatively prime or coprime), then their LCM is simply the product of the two numbers. For example, LCM(15, 28) = 15 x 28 = 420, because GCD(15, 28) = 1.
Q2: Can I find the LCM of more than two numbers?
A2: Yes, the same principles apply. You can extend the prime factorization method or use iterative applications of the GCD/LCM relationship to find the LCM of multiple numbers.
Q3: Are there other methods for finding the LCM?
A3: While the methods described above are the most common and efficient, there are other algorithms and approaches, particularly for very large numbers, that are optimized for computational speed. These often involve more advanced number-theoretic concepts.
Q4: Why is understanding LCM important?
A4: Understanding LCM is essential for building a strong foundation in number theory and for solving a wide range of problems involving divisibility, fractions, and cyclical processes across various disciplines.
Conclusion: Mastering the LCM
Finding the LCM of 14 and 35, as demonstrated, provides a stepping stone to understanding more complex mathematical concepts. The seemingly simple problem opens the door to exploring prime factorization, the Euclidean algorithm, and the elegant relationship between LCM and GCD. Mastering these techniques not only enhances mathematical proficiency but also equips you with tools applicable in various real-world situations. By understanding the underlying principles, you can tackle more complex LCM problems and appreciate the profound influence of number theory in diverse fields. Remember to choose the method best suited to the numbers involved; for smaller numbers, listing multiples might suffice, while prime factorization and the GCD method are more efficient for larger numbers. The key takeaway is not just how to find the LCM but why the methods work, solidifying your understanding of fundamental mathematical principles.
Latest Posts
Latest Posts
-
Pictures Of A Prokaryotic Cell
Sep 11, 2025
-
Number Line With Negative Numbers
Sep 11, 2025
-
Adjacent Angles That Are Supplementary
Sep 11, 2025
-
What Are Factors Of 57
Sep 11, 2025
-
Lcm Of 7 And 21
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 14 And 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.