Lcm Of 13 And 4
seoindie
Sep 12, 2025 · 6 min read
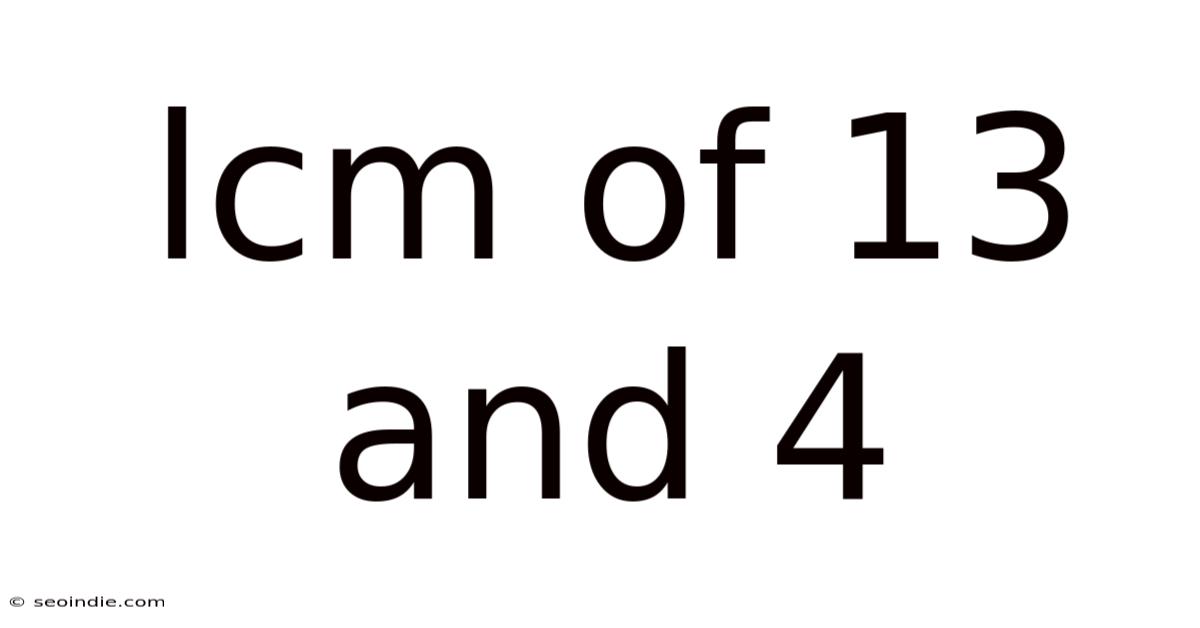
Table of Contents
Finding the Least Common Multiple (LCM) of 13 and 4: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculation can significantly enhance your mathematical abilities. This comprehensive guide will explore various techniques to determine the LCM of 13 and 4, explaining each step in detail and providing a deeper understanding of the principles involved. We'll move beyond a simple answer and delve into the theoretical foundation, making this a valuable resource for students and anyone interested in strengthening their number theory skills.
Introduction: Understanding LCM and its Applications
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. It's a fundamental concept in mathematics with practical applications in various fields, including:
- Fraction Arithmetic: Finding a common denominator when adding or subtracting fractions.
- Scheduling Problems: Determining the time interval when two or more cyclical events coincide (e.g., buses arriving at a stop).
- Music Theory: Calculating the least common multiple of note durations to understand rhythmic patterns.
- Modular Arithmetic: Solving congruences and related problems.
Understanding LCM is crucial for tackling more complex mathematical problems. Let's now explore how to find the LCM of 13 and 4.
Method 1: Listing Multiples
The simplest method to find the LCM involves listing the multiples of each number until a common multiple is found. Let's apply this to 13 and 4:
- Multiples of 13: 13, 26, 39, 52, 65, 78, 91, 104, 117, 130...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60...
By comparing the lists, we observe that the smallest common multiple is 52. Therefore, the LCM(13, 4) = 52. This method works well for smaller numbers but becomes less efficient as the numbers increase in size.
Method 2: Prime Factorization
Prime factorization is a more powerful and efficient method for finding the LCM, especially for larger numbers. This involves breaking down each number into its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
- Prime factorization of 13: 13 is a prime number, so its prime factorization is simply 13.
- Prime factorization of 4: 4 = 2 x 2 = 2²
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the factorizations:
- The prime factor 2 appears with the highest power of 2² in the factorization of 4.
- The prime factor 13 appears with the highest power of 13¹ in the factorization of 13.
Therefore, the LCM(13, 4) = 2² x 13 = 4 x 13 = 52.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are closely related. The GCD is the largest positive integer that divides both numbers without leaving a remainder. There's a convenient formula connecting the LCM and GCD:
LCM(a, b) = (|a x b|) / GCD(a, b)
where |a x b| represents the absolute value of the product of a and b.
Let's find the GCD of 13 and 4 using the Euclidean algorithm:
- Divide the larger number (13) by the smaller number (4): 13 = 3 x 4 + 1
- Replace the larger number with the smaller number (4) and the smaller number with the remainder (1): 4 = 4 x 1 + 0
- The GCD is the last non-zero remainder, which is 1. Therefore, GCD(13, 4) = 1.
Now, we can use the formula:
LCM(13, 4) = (13 x 4) / GCD(13, 4) = 52 / 1 = 52
Method 4: Using the Least Common Multiple Formula Directly
For two numbers 'a' and 'b', a more direct formula exists when the GCD is 1 (as in our case): If GCD(a, b) = 1, then LCM(a, b) = a * b.
Since GCD(13,4) = 1, LCM(13,4) = 13 * 4 = 52
This highlights the efficiency when dealing with coprime numbers (numbers with a GCD of 1).
Explanation of the Methods and their Efficiency
Each method offers a unique approach to finding the LCM. The listing method is intuitive but inefficient for larger numbers. Prime factorization is more efficient and works well for a wider range of numbers, offering a systematic approach to finding the LCM. The method utilizing the GCD provides a powerful link between LCM and GCD, showing the interconnectedness of these fundamental concepts. The direct formula is the quickest when the numbers are coprime. Choosing the best method often depends on the numbers involved and the tools available.
Illustrative Examples: Extending the Concept
Let's apply the prime factorization method to find the LCM of slightly larger numbers:
Example 1: Find the LCM of 12 and 18.
- Prime factorization of 12: 2² x 3
- Prime factorization of 18: 2 x 3²
The highest power of 2 is 2², and the highest power of 3 is 3². Therefore, LCM(12, 18) = 2² x 3² = 4 x 9 = 36.
Example 2: Find the LCM of 24, 36, and 48.
- Prime factorization of 24: 2³ x 3
- Prime factorization of 36: 2² x 3²
- Prime factorization of 48: 2⁴ x 3
The highest power of 2 is 2⁴, and the highest power of 3 is 3². Therefore, LCM(24, 36, 48) = 2⁴ x 3² = 16 x 9 = 144.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between LCM and GCD?
- A: The LCM is the smallest common multiple of two or more numbers, while the GCD is the greatest common divisor. They are related through a formula: LCM(a, b) = (|a x b|) / GCD(a, b).
-
Q: Can the LCM of two numbers be smaller than the larger number?
- A: No. The LCM is always greater than or equal to the largest of the two numbers.
-
Q: What is the LCM of a number and itself?
- A: The LCM of a number and itself is the number itself. For example, LCM(5, 5) = 5.
-
Q: What if one of the numbers is 0?
- A: The LCM of any number and 0 is undefined because 0 has infinitely many multiples.
Conclusion: Mastering LCM for Mathematical Proficiency
Understanding the concept of the least common multiple is essential for various mathematical applications. This guide has explored multiple methods for calculating the LCM, focusing on the numbers 13 and 4 but extending the principles to larger and more complex scenarios. By mastering these techniques and understanding the underlying theoretical framework, you can confidently tackle a wider array of mathematical problems and develop a deeper appreciation for number theory. Remember to choose the most efficient method based on the numbers involved, and don't hesitate to practice regularly to solidify your understanding. From simple fraction addition to more complex scheduling problems, the LCM serves as a fundamental building block for mathematical proficiency.
Latest Posts
Latest Posts
-
Select All That Are Monomers
Sep 12, 2025
-
Derivation Of Equation Of Motion
Sep 12, 2025
-
Questions On Perimeter And Area
Sep 12, 2025
-
Convert 1 3 To Percentage
Sep 12, 2025
-
Metric To Inch Conversion Table
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 13 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.