Lcm Of 12 And 7
seoindie
Sep 25, 2025 · 6 min read
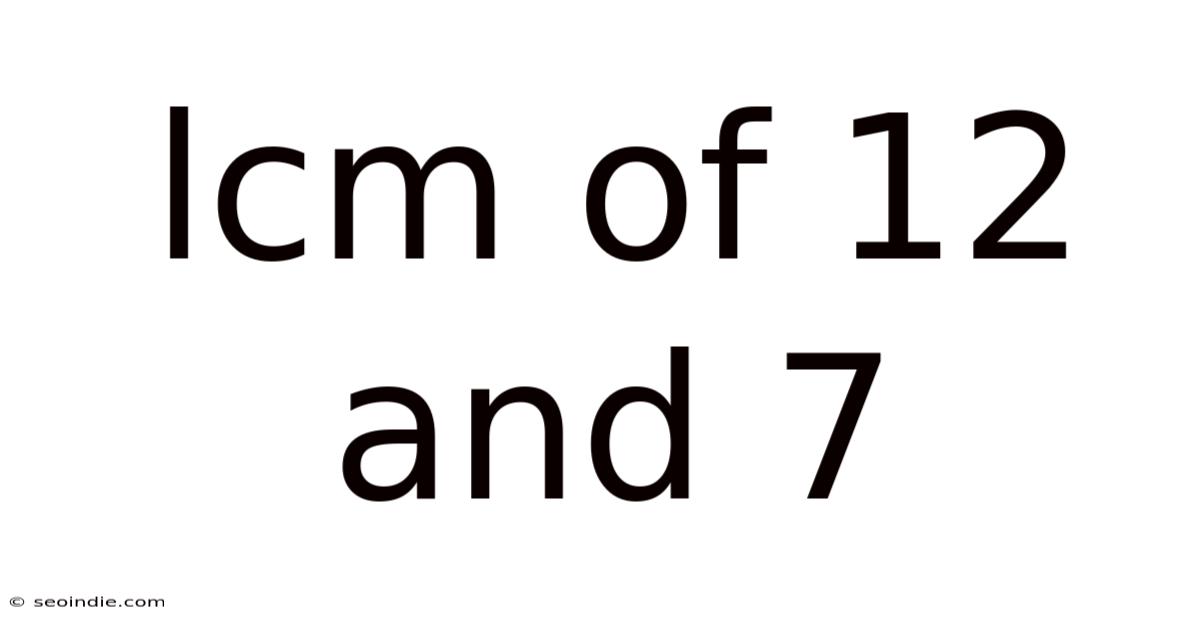
Table of Contents
Finding the Least Common Multiple (LCM) of 12 and 7: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it is crucial for a strong foundation in mathematics. This comprehensive guide will explore the LCM of 12 and 7, demonstrating multiple approaches and delving into the theoretical underpinnings. We'll move beyond a simple answer to equip you with a deeper understanding of this fundamental mathematical concept.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 12 and 7, let's define what the least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the original numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
This concept is fundamental in various mathematical applications, from simplifying fractions to solving problems involving ratios and proportions. Understanding LCM is also crucial for working with periodic phenomena, such as calculating when two events will occur simultaneously.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers like 12 and 7, is listing the multiples of each number until you find the smallest common multiple.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98...
By comparing the lists, we can see that the smallest number appearing in both lists is 84. Therefore, the LCM of 12 and 7 is 84. This method is intuitive and easy to visualize, making it suitable for introductory learning. However, it becomes less efficient with larger numbers.
Method 2: Prime Factorization
A more efficient and powerful method, particularly for larger numbers, involves prime factorization. Prime factorization breaks down a number into its prime factors – numbers divisible only by 1 and themselves.
- Prime Factorize 12: 12 = 2 x 2 x 3 = 2² x 3
- Prime Factorize 7: 7 is a prime number, so its prime factorization is simply 7.
Now, to find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together.
- The prime factors involved are 2, 3, and 7.
- The highest power of 2 is 2² = 4.
- The highest power of 3 is 3¹ = 3.
- The highest power of 7 is 7¹ = 7.
Therefore, the LCM of 12 and 7 is 4 x 3 x 7 = 84. This method is more systematic and readily adaptable to finding the LCM of multiple numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both integers without leaving a remainder. There's a convenient formula linking the LCM and GCD:
LCM(a, b) = (|a x b|) / GCD(a, b)
where 'a' and 'b' are the two integers.
- Find the GCD of 12 and 7: Since 7 is a prime number and doesn't divide 12, the GCD of 12 and 7 is 1.
- Apply the formula: LCM(12, 7) = (|12 x 7|) / 1 = 84.
This method demonstrates the elegant connection between LCM and GCD. Finding the GCD can be done using various methods, including the Euclidean algorithm, which is particularly efficient for larger numbers.
Method 4: Using the Formula Directly (for Two Numbers)
For just two numbers, a simpler formula exists that can be derived from the prime factorization method:
LCM(a, b) = (a * b) / GCD(a, b)
As shown before, the GCD(12, 7) = 1. Therefore, LCM(12, 7) = (12 * 7) / 1 = 84.
This formula offers a direct route to calculating the LCM once you've determined the GCD.
A Deeper Dive into Prime Factorization and its Significance
The prime factorization method highlights the fundamental role of prime numbers in number theory. Every positive integer greater than 1 can be expressed uniquely as a product of prime numbers (Fundamental Theorem of Arithmetic). This unique factorization allows us to systematically analyze the divisibility properties of numbers and efficiently calculate LCMs and GCDs. The prime factorization method scales well for larger numbers and multiple numbers, making it a preferred method in advanced mathematics and computer science.
Applications of LCM in Real-World Scenarios
The concept of LCM extends beyond abstract mathematical exercises. It finds practical applications in various real-world scenarios:
- Scheduling: Imagine two buses depart from the same station, one every 12 minutes and the other every 7 minutes. The LCM (84 minutes) determines when both buses will depart simultaneously again.
- Cyclic Phenomena: In physics and engineering, LCM can help determine the period of combined cyclical events.
- Fraction Simplification: Finding the LCM of the denominators is crucial when adding or subtracting fractions.
Frequently Asked Questions (FAQ)
-
Q: Is there only one LCM for two numbers?
- A: Yes, there is only one least common multiple for any pair of numbers.
-
Q: What if one of the numbers is 0?
- A: The LCM is undefined when one of the numbers is 0.
-
Q: How can I find the LCM of more than two numbers?
- A: You can extend the prime factorization method or use iterative approaches. Find the LCM of the first two numbers, then find the LCM of that result and the third number, and so on.
-
Q: Is there a calculator or software that can find the LCM?
- A: Yes, many online calculators and mathematical software packages can calculate the LCM efficiently. However, understanding the underlying methods is crucial for a deeper appreciation of the concept.
-
Q: Why is the prime factorization method considered more efficient for larger numbers?
- A: Listing multiples becomes increasingly tedious and inefficient with larger numbers. Prime factorization provides a structured and systematic approach that scales better, especially when dealing with many numbers or very large numbers.
Conclusion
Calculating the LCM of 12 and 7, although seemingly simple, provides a gateway to understanding fundamental concepts in number theory and their practical applications. The various methods presented, from listing multiples to utilizing prime factorization and the GCD, illustrate the interconnectedness of mathematical ideas. Mastering these methods will empower you to tackle more complex problems involving LCMs and GCDs, strengthening your mathematical foundation and preparing you for advanced mathematical studies. Remember, the key is not just to get the answer (84 in this case) but to understand why the answer is what it is and the various paths to arrive at it. This understanding allows you to apply the concept of LCM effectively in diverse contexts.
Latest Posts
Latest Posts
-
What Is Natural Gas Advantages
Sep 25, 2025
-
Fruits Start With Letter A
Sep 25, 2025
-
170 000 Km In Miles
Sep 25, 2025
-
Greatest Common Factor Of 80
Sep 25, 2025
-
Words That Start With Gla
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 12 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.