Lcm Of 12 And 32
seoindie
Sep 16, 2025 · 6 min read
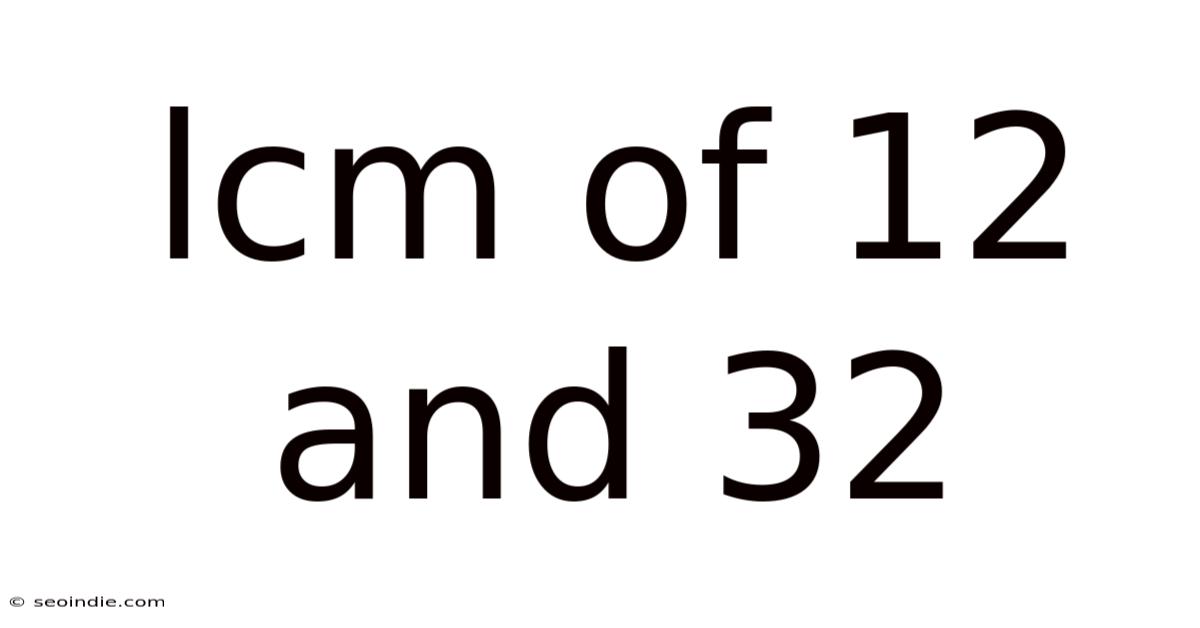
Table of Contents
Finding the Least Common Multiple (LCM) of 12 and 32: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it can significantly improve your mathematical skills and problem-solving abilities. This comprehensive guide will delve into the process of determining the LCM of 12 and 32, exploring various approaches and providing a deeper understanding of the mathematical principles involved. We'll cover everything from basic definitions to advanced techniques, ensuring you grasp the concept fully.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) is the smallest positive integer that is a multiple of two or more numbers. In simpler terms, it's the smallest number that can be divided evenly by all the numbers in question without leaving a remainder. Understanding the LCM is crucial in various mathematical applications, including simplifying fractions, solving problems involving time and cycles, and working with ratios and proportions. This article focuses on finding the LCM of 12 and 32, providing several methods to achieve this, catering to different learning styles and mathematical backgrounds.
Method 1: Listing Multiples
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 160, 192, ...
- Multiples of 32: 32, 64, 96, 128, 160, 192, 224, ...
By comparing the lists, we can see that the smallest number appearing in both lists is 96. Therefore, the LCM of 12 and 32 is 96. This method is simple to visualize but becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors. Prime factors are prime numbers that, when multiplied together, result in the original number.
-
Prime Factorization of 12: 12 = 2 x 2 x 3 = 2² x 3
-
Prime Factorization of 32: 32 = 2 x 2 x 2 x 2 x 2 = 2⁵
-
Finding the LCM: To find the LCM using prime factorization, we take the highest power of each prime factor present in either factorization and multiply them together.
In this case, the prime factors are 2 and 3. The highest power of 2 is 2⁵ (from 32), and the highest power of 3 is 3¹ (from 12).
Therefore, LCM(12, 32) = 2⁵ x 3¹ = 32 x 3 = 96
This method is more systematic and less prone to error, especially when dealing with larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are closely related. There's a formula that connects them:
LCM(a, b) = (|a x b|) / GCD(a, b)
where |a x b| represents the absolute value of the product of a and b.
-
Finding the GCD of 12 and 32: We can use the Euclidean algorithm to find the GCD.
- Divide 32 by 12: 32 = 2 x 12 + 8
- Divide 12 by the remainder 8: 12 = 1 x 8 + 4
- Divide 8 by the remainder 4: 8 = 2 x 4 + 0
The last non-zero remainder is 4, so the GCD(12, 32) = 4.
-
Calculating the LCM: Now we can use the formula:
LCM(12, 32) = (12 x 32) / 4 = 384 / 4 = 96
This method is efficient and elegantly connects the concepts of LCM and GCD. The Euclidean algorithm is particularly useful for finding the GCD of larger numbers.
Method 4: Using a Least Common Multiple Calculator (For Verification)
While it's essential to understand the underlying mathematical principles, using a calculator can be a handy tool for verification, especially when dealing with more complex scenarios or larger numbers. Many online calculators are available to compute the LCM of two or more numbers. Inputting 12 and 32 will confirm that the LCM is indeed 96. However, relying solely on calculators without understanding the methods can hinder your mathematical understanding.
A Deeper Dive into Prime Factorization and its Significance
The prime factorization method is not just a convenient way to calculate the LCM; it reveals the fundamental building blocks of numbers. Understanding prime factorization helps us understand the properties of numbers and their relationships. Every positive integer can be uniquely expressed as a product of prime numbers (Fundamental Theorem of Arithmetic). This unique factorization allows us to easily compare and contrast numbers, analyze their divisors, and determine their LCM and GCD efficiently.
Real-World Applications of LCM
The concept of LCM finds practical applications in various real-world scenarios:
-
Scheduling: Imagine two buses that depart from the same station, one every 12 minutes and the other every 32 minutes. The LCM (96 minutes) represents the time when both buses will depart simultaneously again.
-
Construction: If you have tiles of two different lengths (12 inches and 32 inches), the LCM will determine the smallest length of a wall that can be perfectly tiled with either size without any cuts or gaps.
-
Cooking: If a recipe calls for ingredients to be added at intervals of 12 minutes and 32 minutes, understanding the LCM helps determine when both ingredients are added concurrently.
-
Music: Understanding musical rhythms and intervals frequently involves LCM to find the smallest common period or beat.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers have no common factors?
- A: If two numbers are relatively prime (they share no common factors other than 1), their LCM is simply their product. For example, LCM(15, 28) = 15 x 28 = 420.
-
Q: Can the LCM be larger than the product of the numbers?
- A: No, the LCM is always less than or equal to the product of the numbers.
-
Q: Is there a difference between LCM and GCD?
- A: Yes, LCM is the smallest common multiple, while GCD is the greatest common divisor. They are related but represent different aspects of the numbers' relationship.
-
Q: How can I improve my understanding of LCM and GCD?
- A: Practice is key. Try calculating the LCM and GCD of various pairs of numbers using different methods. This will build your familiarity and confidence. Exploring online resources and interactive exercises can also be beneficial.
Conclusion:
Finding the least common multiple (LCM) of 12 and 32, or any pair of numbers, is a fundamental skill in mathematics. We've explored several methods, from listing multiples to prime factorization and using the GCD. The prime factorization method provides a deeper understanding of the underlying mathematical principles and is generally the most efficient for larger numbers. Remember that choosing the right method depends on the context and the complexity of the numbers involved. Mastering the LCM calculation enhances problem-solving skills across various mathematical domains and has practical applications in diverse real-world scenarios. Through practice and a solid understanding of the concepts, you can confidently tackle more complex LCM problems and appreciate the elegant simplicity of this important mathematical concept.
Latest Posts
Latest Posts
-
Questions On Area Of Parallelogram
Sep 16, 2025
-
One Hundred And Forty Dollars
Sep 16, 2025
-
5mm Equals How Many Cm
Sep 16, 2025
-
Potassium Oxide Ionic Or Covalent
Sep 16, 2025
-
The End Of A River
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 12 And 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.