Lcm Of 12 And 28
seoindie
Sep 19, 2025 · 6 min read
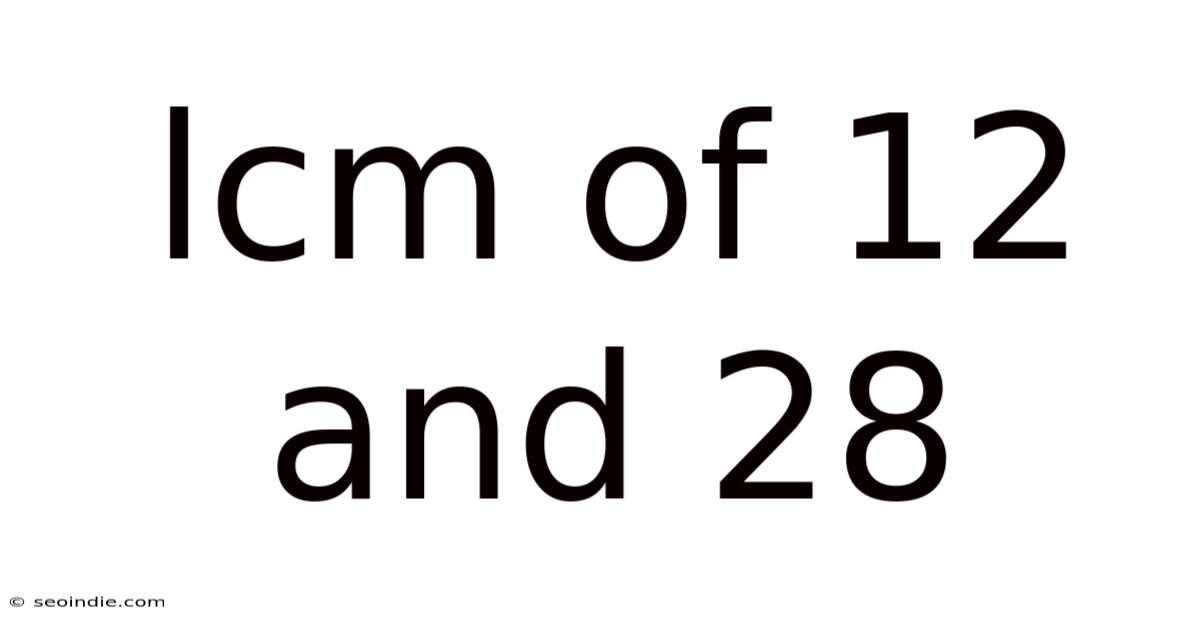
Table of Contents
Finding the Least Common Multiple (LCM) of 12 and 28: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles and various methods to calculate it can be surprisingly insightful. This article will delve into the concept of LCM, focusing on how to find the LCM of 12 and 28 using different approaches. We'll explore the prime factorization method, the listing multiples method, and the greatest common divisor (GCD) method, providing a thorough understanding of each. We'll also address common questions and misconceptions, ensuring a complete grasp of this fundamental mathematical concept.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that is a multiple of all the given numbers. Understanding LCM is crucial in various mathematical contexts, including simplifying fractions, solving problems involving cycles or repeating events, and working with ratios and proportions. This article will specifically address how to find the LCM of 12 and 28, using multiple methods to illustrate the versatility of this mathematical concept.
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers like 12 and 28. It involves listing the multiples of each number until you find the smallest common multiple.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156, 168...
- Multiples of 28: 28, 56, 84, 112, 140, 168, 196, 224...
By comparing the lists, we can see that the smallest number that appears in both lists is 84. Therefore, the LCM of 12 and 28 is 84.
While this method works well for smaller numbers, it becomes less efficient as the numbers increase in size. For larger numbers, more efficient methods are preferred.
Method 2: Prime Factorization
This method uses the prime factorization of each number to find the LCM. Prime factorization is the process of expressing a number as a product of its prime factors.
- Prime factorization of 12: 12 = 2 x 2 x 3 = 2² x 3
- Prime factorization of 28: 28 = 2 x 2 x 7 = 2² x 7
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations of both numbers and multiply them together.
In this case, the prime factors are 2, 3, and 7. The highest power of 2 is 2² (from both 12 and 28), the highest power of 3 is 3¹ (from 12), and the highest power of 7 is 7¹ (from 28).
Therefore, the LCM of 12 and 28 is: 2² x 3 x 7 = 4 x 3 x 7 = 84
This method is generally more efficient than listing multiples, especially for larger numbers. It provides a structured approach that avoids the tedious process of manually listing multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The GCD (Greatest Common Divisor), also known as the highest common factor (HCF), is the largest number that divides both given numbers without leaving a remainder. There's a useful relationship between the LCM and GCD of two numbers:
LCM(a, b) x GCD(a, b) = a x b
First, we need to find the GCD of 12 and 28. We can use the Euclidean algorithm for this:
- Divide the larger number (28) by the smaller number (12): 28 ÷ 12 = 2 with a remainder of 4.
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (4): 12 ÷ 4 = 3 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 4.
Now we can use the formula:
LCM(12, 28) x GCD(12, 28) = 12 x 28 LCM(12, 28) x 4 = 336 LCM(12, 28) = 336 ÷ 4 = 84
This method provides an alternative approach to finding the LCM, particularly useful when you already know or can easily calculate the GCD of the numbers.
Understanding the Concept of Multiples
A multiple of a number is the result of multiplying that number by any integer. For example:
- Multiples of 12: 12, 24, 36, 48, 60, and so on.
- Multiples of 28: 28, 56, 84, 112, 140, and so on.
The LCM is the smallest positive number that is found in both lists of multiples.
Real-World Applications of LCM
The concept of LCM has practical applications in various scenarios:
- Scheduling: Imagine two buses arrive at a bus stop at different intervals. The LCM helps determine when both buses will arrive at the stop simultaneously.
- Project Management: If different tasks in a project take varying amounts of time to complete, the LCM can help schedule the tasks efficiently.
- Music: The LCM is used in music theory to determine when different musical rhythms align.
- Fractions: Finding the LCM is essential when adding or subtracting fractions with different denominators.
Frequently Asked Questions (FAQ)
Q1: What if the two numbers are prime numbers?
If the two numbers are prime (meaning their only divisors are 1 and themselves), their LCM is simply their product. For example, the LCM of 2 and 7 is 14 (2 x 7).
Q2: Can the LCM of two numbers be smaller than the largest of the two numbers?
No. The LCM of two numbers is always greater than or equal to the larger of the two numbers.
Q3: Is there a formula for finding the LCM of more than two numbers?
Yes. While the methods described above primarily focus on two numbers, the prime factorization method can be easily extended to find the LCM of more than two numbers. You would still identify the prime factors of each number and then multiply the highest power of each distinct prime factor.
Q4: What if one of the numbers is zero?
The LCM of any number and zero is undefined.
Conclusion:
Finding the LCM of 12 and 28, as demonstrated, is achievable through various methods. The most efficient methods, particularly for larger numbers, are the prime factorization method and the method using the GCD. Understanding these methods and the underlying concepts of multiples, prime factors, and the relationship between LCM and GCD empowers you to tackle more complex mathematical problems confidently. The applications of LCM extend far beyond simple arithmetic exercises, playing a vital role in solving real-world problems across diverse fields. Mastering this concept solidifies a foundational understanding of number theory and its practical implications. Remember to choose the method that best suits the given numbers and your comfort level with different mathematical techniques. Practice will further enhance your understanding and speed in calculating the LCM of any pair of integers.
Latest Posts
Latest Posts
-
Metric Imperial Measurement Conversion Chart
Sep 20, 2025
-
Characteristics That Start With R
Sep 20, 2025
-
Cubic Inches To Liters Calculator
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 12 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.