Lcm Of 12 And 2
seoindie
Sep 16, 2025 · 6 min read
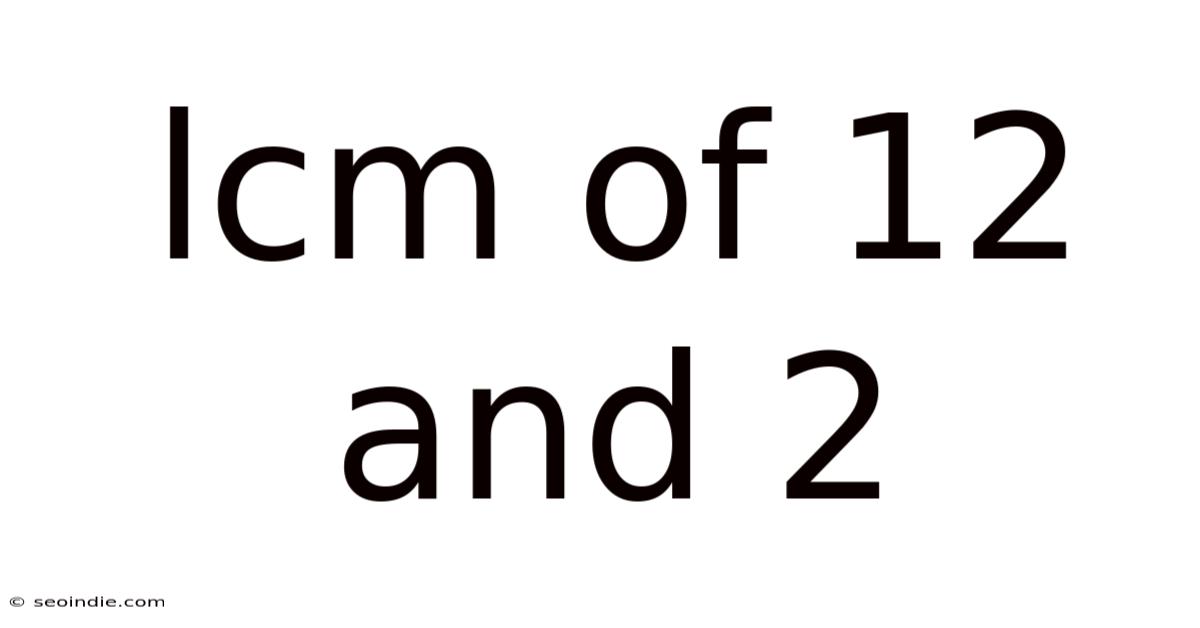
Table of Contents
Understanding the Least Common Multiple (LCM): A Deep Dive into the LCM of 12 and 2
Finding the Least Common Multiple (LCM) might seem like a simple mathematical task, especially when dealing with small numbers like 12 and 2. However, understanding the underlying concepts and various methods for calculating the LCM is crucial for grasping more advanced mathematical concepts. This article will delve deep into the LCM of 12 and 2, exploring different approaches, providing a solid theoretical foundation, and addressing frequently asked questions. This comprehensive guide will equip you with the knowledge to confidently tackle LCM problems involving any set of numbers.
Introduction to Least Common Multiple (LCM)
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. Understanding the LCM is vital in various mathematical applications, including simplifying fractions, solving problems involving fractions and ratios, and understanding rhythmic patterns in music.
Methods for Finding the LCM of 12 and 2
There are several effective methods to calculate the LCM of 12 and 2. Let's explore the most common ones:
1. Listing Multiples Method:
This is a straightforward method, especially suitable for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 12: 12, 24, 36, 48, 60, ...
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, ...
By comparing the lists, we can see that the smallest number present in both lists is 12. Therefore, the LCM of 12 and 2 is 12.
2. Prime Factorization Method:
This method is more efficient for larger numbers and provides a deeper understanding of the concept. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
- Prime factorization of 12: 2² x 3
- Prime factorization of 2: 2
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
Therefore, the LCM of 12 and 2 is 2² x 3 = 4 x 3 = 12.
3. Greatest Common Divisor (GCD) Method:
This method utilizes the relationship between the LCM and the Greatest Common Divisor (GCD) of two numbers. The formula is:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two numbers.
- GCD(a, b) is the Greatest Common Divisor of a and b. The GCD is the largest number that divides both a and b without leaving a remainder.
Let's apply this to 12 and 2:
- GCD(12, 2) = 2 (because 2 is the largest number that divides both 12 and 2)
- LCM(12, 2) = (12 x 2) / 2 = 24 / 2 = 12
This method elegantly connects the concepts of LCM and GCD, highlighting their interconnectedness.
A Deeper Look into the Mathematical Concepts
The LCM is fundamentally linked to the concept of divisibility. A number 'a' is divisible by another number 'b' if the remainder is 0 when 'a' is divided by 'b'. The LCM represents the smallest number that satisfies the divisibility condition for all the numbers in a given set.
The prime factorization method provides a powerful insight into the structure of numbers. Every integer greater than 1 can be expressed as a unique product of prime numbers (numbers divisible only by 1 and themselves). By understanding the prime factorization, we can efficiently determine the LCM, as it's simply a matter of combining the highest powers of all prime factors.
The GCD method demonstrates a fundamental relationship between the LCM and GCD. These two concepts are inversely proportional in a way; as the GCD increases, the LCM decreases, and vice versa. This relationship is encapsulated in the formula mentioned earlier and is a testament to the interconnectedness of mathematical concepts.
Applications of LCM in Real-World Scenarios
The LCM has far-reaching applications beyond the classroom:
- Scheduling: Imagine two buses depart from the same station, one every 12 minutes and the other every 2 minutes. The LCM (12) helps determine when both buses will depart simultaneously again.
- Fraction Operations: Finding the LCM of the denominators is crucial when adding or subtracting fractions. It allows you to find a common denominator, making the operation straightforward.
- Rhythmic Patterns: In music, the LCM helps determine when rhythmic patterns repeat themselves simultaneously. For instance, understanding the LCM of different note durations allows musicians to create complex yet harmonious rhythmic structures.
- Manufacturing and Production: In manufacturing, the LCM can help optimize production schedules by determining when different machines or processes will align for efficient operation.
Frequently Asked Questions (FAQ)
Q1: What if one of the numbers is 0?
A1: The LCM of any number and 0 is undefined. The concept of multiples does not apply to 0.
Q2: How do I find the LCM of more than two numbers?
A2: You can extend the prime factorization or GCD methods to handle multiple numbers. For prime factorization, you consider all prime factors present in the factorizations of all the numbers and take the highest power of each. For the GCD method, you can iteratively apply it to pairs of numbers, reducing the set until you have the LCM of all numbers.
Q3: Is there a shortcut for finding the LCM of two numbers if one is a multiple of the other?
A3: Yes! If one number is a multiple of the other, the larger number is the LCM. For instance, since 12 is a multiple of 2, the LCM of 12 and 2 is 12.
Q4: Why is understanding LCM important?
A4: Understanding LCM is fundamental to many areas of mathematics and its applications. It's crucial for working with fractions, solving problems involving ratios and proportions, and even understanding complex rhythmic structures in music. It's a building block for more advanced mathematical concepts.
Conclusion
Finding the LCM of 12 and 2, although seemingly straightforward, serves as an excellent introduction to the broader concept of Least Common Multiples. Through various methods, from listing multiples to employing prime factorization and the GCD relationship, we've explored this fundamental mathematical concept thoroughly. Understanding the LCM is not just about memorizing formulas but grasping the underlying principles of divisibility and the structure of numbers. This knowledge empowers you to tackle more complex mathematical problems and appreciate the interconnectedness of mathematical concepts in various fields. Remember, the journey of learning mathematics is a continuous exploration, and understanding core concepts like the LCM is the key to unlocking more advanced mathematical knowledge.
Latest Posts
Latest Posts
-
Words With Y And Q
Sep 16, 2025
-
Physical Mapping Vs Genetic Mapping
Sep 16, 2025
-
3 8 Into A Percent
Sep 16, 2025
-
1990 In Roman Numerals Tattoo
Sep 16, 2025
-
Net Investment Vs Gross Investment
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 12 And 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.