Lcm Of 12 And 13
seoindie
Sep 13, 2025 · 5 min read
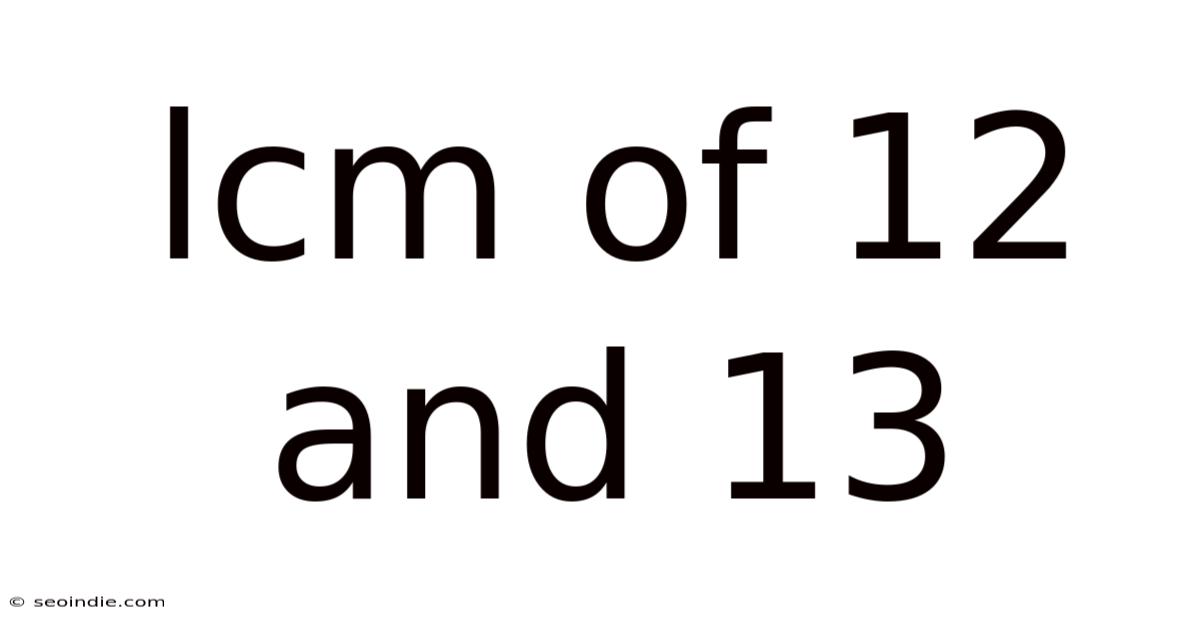
Table of Contents
Finding the Least Common Multiple (LCM) of 12 and 13: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, especially with smaller numbers like 12 and 13. However, understanding the underlying concepts and different methods for calculating the LCM provides a strong foundation for more complex mathematical problems. This article will explore various approaches to finding the LCM of 12 and 13, delve into the theoretical background, and even touch upon applications in real-world scenarios. We'll also answer some frequently asked questions to ensure a comprehensive understanding of this fundamental mathematical concept.
Understanding Least Common Multiple (LCM)
Before we jump into calculating the LCM of 12 and 13, let's define what it actually means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number that is divisible by both 2 and 3.
Methods for Calculating the LCM of 12 and 13
There are several ways to find the LCM, each with its own advantages and disadvantages. Let's explore three common methods:
1. Listing Multiples Method
This is a straightforward approach, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156...
- Multiples of 13: 13, 26, 39, 52, 65, 78, 91, 104, 117, 130, 143, 156...
Notice that 156 is the smallest number that appears in both lists. Therefore, the LCM of 12 and 13 is 156. This method is easy to visualize but can become tedious with larger numbers.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. The prime factorization is the expression of a number as a product of its prime factors.
- Prime factorization of 12: 2² x 3
- Prime factorization of 13: 13 (13 is a prime number)
To find the LCM using prime factorization, we take the highest power of each prime factor present in either factorization and multiply them together. In this case:
LCM(12, 13) = 2² x 3 x 13 = 4 x 3 x 13 = 156
This method is more efficient for larger numbers, as it avoids the lengthy process of listing multiples.
3. Greatest Common Divisor (GCD) Method
This method uses the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers evenly. The formula connecting LCM and GCD is:
LCM(a, b) = (|a x b|) / GCD(a, b)
First, we need to find the GCD of 12 and 13. Since 13 is a prime number and doesn't divide 12, the GCD(12, 13) = 1. (Remember, 1 is a divisor of every number.)
Now, we can apply the formula:
LCM(12, 13) = (12 x 13) / 1 = 156
This method is efficient, especially when dealing with larger numbers where finding the GCD using the Euclidean algorithm is faster than listing multiples or finding prime factorizations.
A Deeper Dive into Prime Factorization
The prime factorization method is particularly insightful for understanding the structure of numbers and their relationships. Let's revisit the prime factorization of 12 and 13:
- 12 = 2² x 3
- 13 = 13
The prime factorization reveals the fundamental building blocks of these numbers. 12 is composed of two 2s and one 3, while 13 is simply 13. The LCM is essentially constructing the "largest" number that contains all the prime factors of both 12 and 13, taking the highest power of each. This explains why we multiply 2², 3, and 13 to get the LCM of 156.
Applications of LCM in Real-World Scenarios
While finding the LCM of 12 and 13 might seem abstract, the concept of LCM has practical applications in various fields:
-
Scheduling: Imagine you have two machines that operate on different cycles. One machine completes a task every 12 minutes, and the other every 13 minutes. To find the time when both machines complete a task simultaneously, you would calculate the LCM(12, 13) = 156 minutes. This is the time they will both be finished at the same moment.
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator.
-
Modular Arithmetic: LCM plays a significant role in various areas of modular arithmetic and cryptography, helping determine patterns and periodicities.
-
Patterning and Sequencing: LCM can be useful in problems involving repetitive events or cycles where you need to find the next point of synchronization.
Frequently Asked Questions (FAQ)
Q: Is the LCM always greater than the numbers involved?
A: Yes, unless one number is a multiple of the other. If one number is a multiple of the other, the LCM will be the larger number. For example, LCM(4, 8) = 8.
Q: Can we find the LCM of more than two numbers?
A: Absolutely. The prime factorization method readily extends to multiple numbers. We find the prime factorization of each number and then take the highest power of each prime factor present in any of the factorizations. For example, to find the LCM(4, 6, 9), we would consider 2², 3², and combine them to get LCM(4, 6, 9) = 36.
Q: What if the numbers have no common factors other than 1?
A: If the numbers are coprime (meaning their GCD is 1), their LCM is simply their product. This is the case with 12 and 13, as their GCD is 1, and their LCM is 12 x 13 = 156.
Conclusion
Finding the LCM of 12 and 13, while seemingly a simple problem, provides a valuable opportunity to explore several mathematical concepts and methodologies. Understanding the underlying principles of LCM, including prime factorization and the relationship between LCM and GCD, is crucial for tackling more complex mathematical challenges. The various methods presented, along with the practical applications discussed, emphasize the importance of this fundamental concept in various fields, highlighting its relevance beyond the confines of the classroom. Remember that mastering these basic mathematical concepts lays a solid groundwork for advanced studies and real-world problem-solving.
Latest Posts
Latest Posts
-
How To Find Intial Velocity
Sep 13, 2025
-
How Do You Spell 63
Sep 13, 2025
-
Perimeter Of A Semi Circle
Sep 13, 2025
-
What Numbers Go Into 72
Sep 13, 2025
-
Bank Phone Number Change Letter
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 12 And 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.