Lcm Of 11 And 7
seoindie
Sep 17, 2025 · 6 min read
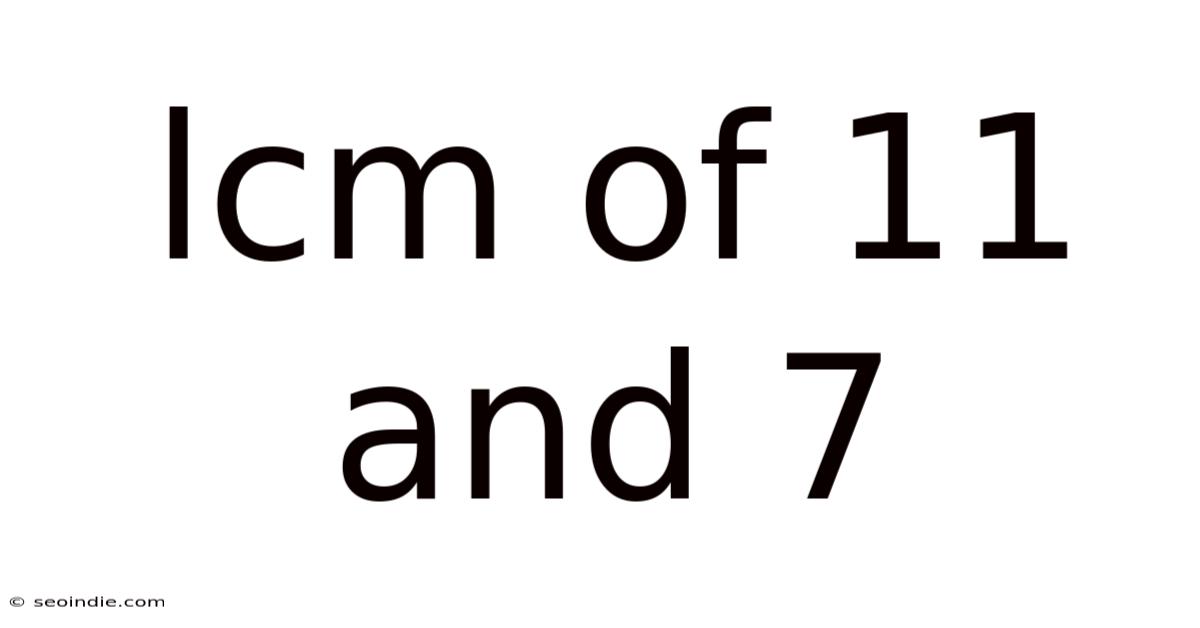
Table of Contents
Unveiling the Least Common Multiple (LCM) of 11 and 7: A Deep Dive into Number Theory
Finding the Least Common Multiple (LCM) might seem like a simple arithmetic task, especially when dealing with small numbers like 11 and 7. However, understanding the underlying principles and various methods for calculating the LCM reveals a fascinating glimpse into number theory. This article will not only show you how to find the LCM of 11 and 7 but also explore the broader concepts behind it, providing a comprehensive understanding suitable for students and anyone curious about the beauty of mathematics. We'll cover different approaches, explain the reasoning behind them, and answer frequently asked questions, ensuring a complete and engaging learning experience.
Understanding Least Common Multiples (LCM)
Before we delve into the specific case of 11 and 7, let's establish a solid foundation. The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the given integers. Think of it as the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6, because 6 is the smallest positive integer that is divisible by both 2 and 3.
This concept is crucial in various mathematical applications, including:
- Fraction simplification: Finding the LCM of denominators helps in adding or subtracting fractions efficiently.
- Solving equations: LCM is used in solving equations involving fractions or rational expressions.
- Scheduling problems: Determining when events that occur at regular intervals will coincide (e.g., buses arriving at a stop).
- Music theory: Understanding rhythms and harmonies often involves finding the LCM of different note durations.
Method 1: Listing Multiples
The most straightforward method, especially for small numbers like 11 and 7, is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105...
By comparing the lists, we can see that the smallest number appearing in both lists is 77. Therefore, the LCM of 11 and 7 is 77.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the concept. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all the prime factors present.
- Prime factorization of 11: 11 is a prime number, so its prime factorization is simply 11.
- Prime factorization of 7: 7 is also a prime number, so its prime factorization is 7.
Since 11 and 7 are both prime numbers and have no common factors other than 1, the LCM is simply the product of the two numbers. Therefore, LCM(11, 7) = 11 x 7 = 77.
Method 3: Using the Formula (For Two Numbers)
For two numbers, 'a' and 'b', there's a convenient formula that relates the LCM and the Greatest Common Divisor (GCD):
LCM(a, b) = (|a * b|) / GCD(a, b)
Where:
- |a * b| represents the absolute value of the product of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
Let's apply this to 11 and 7:
- GCD(11, 7) = 1 (since 11 and 7 are coprime – they share no common factors other than 1).
- LCM(11, 7) = (11 * 7) / 1 = 77
Method 4: Euclidean Algorithm (For finding GCD, then using the formula)
The Euclidean Algorithm is an efficient method for finding the GCD of two numbers. While we already know the GCD of 11 and 7 is 1, let's demonstrate the algorithm:
- Divide the larger number (11) by the smaller number (7): 11 = 1 * 7 + 4
- Replace the larger number with the smaller number (7) and the smaller number with the remainder (4): 7 = 1 * 4 + 3
- Repeat: 4 = 1 * 3 + 1
- Repeat: 3 = 3 * 1 + 0
The last non-zero remainder is the GCD, which is 1. Then, using the formula from Method 3, we get LCM(11, 7) = (11 * 7) / 1 = 77. This method is particularly useful for finding the LCM of larger numbers where finding the prime factorization might be more challenging.
The Significance of Coprime Numbers
The numbers 11 and 7 are examples of coprime numbers (also known as relatively prime numbers). Coprime numbers are integers that have a greatest common divisor (GCD) of 1. This means they share no common factors other than 1. When two numbers are coprime, their LCM is simply the product of the two numbers. This simplifies the calculation considerably.
Extending to More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, you would find the prime factorization of each number and then include the highest power of each prime factor present in the final LCM. For the formula method, you would need to employ iterative approaches or more advanced algorithms to handle multiple numbers efficiently.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
A1: The Least Common Multiple (LCM) is the smallest positive integer that is divisible by all the given integers. The Greatest Common Divisor (GCD) is the largest positive integer that divides all the given integers without leaving a remainder. They are inversely related; a larger GCD implies a smaller LCM, and vice-versa.
Q2: Can the LCM of two numbers be greater than their product?
A2: No. The LCM of two numbers is always less than or equal to their product. Equality holds only when the numbers are coprime.
Q3: Are there any real-world applications of LCM beyond mathematics?
A3: Yes! LCM is used in various real-world scenarios. For instance, in scheduling, determining when two events that recur at different intervals will occur simultaneously (like the meeting of two buses on a route). It is also used in manufacturing to synchronize production cycles.
Conclusion
Finding the LCM of 11 and 7, while seemingly simple, serves as a gateway to understanding fundamental concepts in number theory. We've explored multiple methods—listing multiples, prime factorization, using the LCM/GCD formula, and the Euclidean algorithm—illustrating the versatility and efficiency of different approaches. Understanding these methods provides a solid foundation for tackling more complex problems involving LCM and GCD. Remember that the key is to grasp the underlying principles, allowing you to choose the most appropriate method depending on the context and the size of the numbers involved. This journey into the world of LCM hopefully enhances your mathematical understanding and appreciation for the elegance of numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 11 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.