Lcm Of 10 And 3
seoindie
Sep 14, 2025 · 5 min read
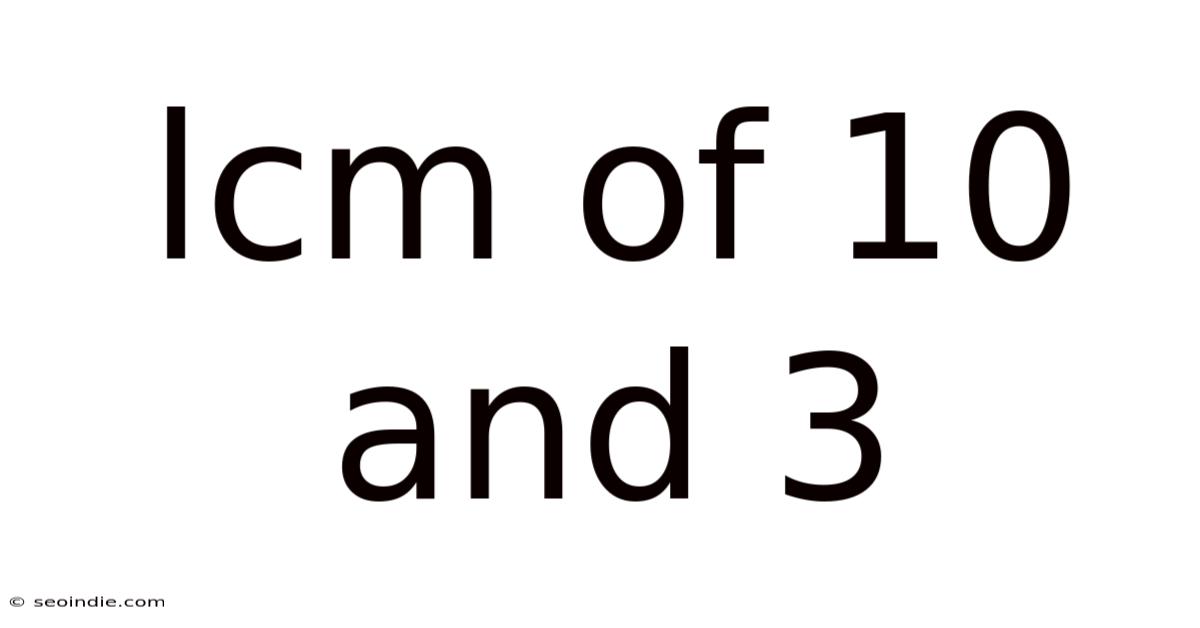
Table of Contents
Finding the Least Common Multiple (LCM) of 10 and 3: A Deep Dive
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts reveals a fascinating glimpse into number theory. This article delves into the process of calculating the LCM of 10 and 3, explaining various methods and exploring their mathematical foundations. We'll go beyond a simple answer and uncover the 'why' behind the calculations, making this concept accessible to everyone, regardless of their mathematical background. This comprehensive guide will equip you with a solid understanding of LCM, its applications, and how to tackle similar problems with confidence.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers you're considering as factors. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3. Understanding LCM is crucial in various mathematical applications, from simplifying fractions to solving problems involving cycles and periodic events.
Method 1: Listing Multiples
The most straightforward method to find the LCM of 10 and 3 is by listing their multiples until a common multiple is found.
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33...
By comparing the lists, we observe that the smallest number appearing in both lists is 30. Therefore, the LCM of 10 and 3 is 30. This method is simple for smaller numbers but becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
A more efficient and mathematically elegant method involves prime factorization. This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers (ignoring the order).
Step 1: Find the prime factorization of each number.
- 10: The prime factorization of 10 is 2 x 5.
- 3: The prime factorization of 3 is simply 3 (as 3 is a prime number).
Step 2: Identify the highest power of each prime factor present in the factorizations.
In our case, the prime factors are 2, 3, and 5. The highest powers are:
- 2¹
- 3¹
- 5¹
Step 3: Multiply the highest powers together.
LCM(10, 3) = 2¹ x 3¹ x 5¹ = 30
This method is significantly more efficient for larger numbers because it avoids the lengthy process of listing multiples. It provides a structured approach that directly links to the fundamental building blocks of number theory.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of two numbers are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers.
Step 1: Find the GCD of 10 and 3 using the Euclidean Algorithm.
The Euclidean Algorithm is a highly efficient method for finding the GCD. It involves repeatedly applying the division algorithm until the remainder is 0.
- Divide the larger number (10) by the smaller number (3): 10 = 3 x 3 + 1
- Replace the larger number with the smaller number (3) and the smaller number with the remainder (1): 3 = 1 x 3 + 0
The last non-zero remainder is the GCD, which is 1. Therefore, GCD(10, 3) = 1.
Step 2: Apply the formula:
LCM(10, 3) x GCD(10, 3) = 10 x 3 LCM(10, 3) x 1 = 30 LCM(10, 3) = 30
Why is the LCM Important?
The LCM has numerous applications across various fields:
-
Fraction Arithmetic: When adding or subtracting fractions with different denominators, finding the LCM of the denominators helps in finding the least common denominator (LCD), simplifying the calculation process.
-
Scheduling and Cyclical Events: Imagine two events happening at different intervals. The LCM helps determine when both events will occur simultaneously. For example, if event A happens every 10 days and event B happens every 3 days, they will coincide every 30 days (the LCM of 10 and 3).
-
Modular Arithmetic: LCM plays a critical role in modular arithmetic, a branch of number theory dealing with remainders after division.
-
Computer Science: LCM finds applications in algorithms related to scheduling tasks, memory management, and data structures.
Frequently Asked Questions (FAQ)
Q1: What if the two numbers are the same?
If the two numbers are identical, their LCM is simply the number itself. For example, LCM(5, 5) = 5.
Q2: Can the LCM be larger than both numbers?
Yes, the LCM is always greater than or equal to the larger of the two numbers. It's only equal if one number is a multiple of the other.
Q3: What if one of the numbers is 0?
The LCM of any number and 0 is undefined because 0 is a divisor of every number, leading to an infinite number of common multiples.
Q4: Can I use a calculator to find the LCM?
Many scientific calculators have a built-in function to calculate the LCM. However, understanding the underlying methods is crucial for comprehending the concept and solving problems effectively, even without a calculator.
Conclusion
Finding the LCM of 10 and 3, while seemingly simple, opens doors to a deeper understanding of fundamental mathematical concepts. We explored three distinct methods – listing multiples, prime factorization, and using the GCD – each offering a unique perspective on the problem. Understanding these methods not only equips you with the ability to calculate LCMs but also provides a solid foundation for tackling more complex number theory problems. Remember, the key to mastering this concept lies not just in finding the answer but in understanding why the methods work, enhancing your overall mathematical intuition. The ability to confidently calculate LCMs is an invaluable skill across various disciplines, proving that even seemingly simple arithmetic holds surprising depth and relevance.
Latest Posts
Latest Posts
-
Area And Perimeter Of Triangle
Sep 14, 2025
-
Objects That Begin With T
Sep 14, 2025
-
M M X I V
Sep 14, 2025
-
7 Times 7 Times 7
Sep 14, 2025
-
Algebra Equations That Equal 16
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 10 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.