Lcm For 15 And 9
seoindie
Sep 21, 2025 · 6 min read
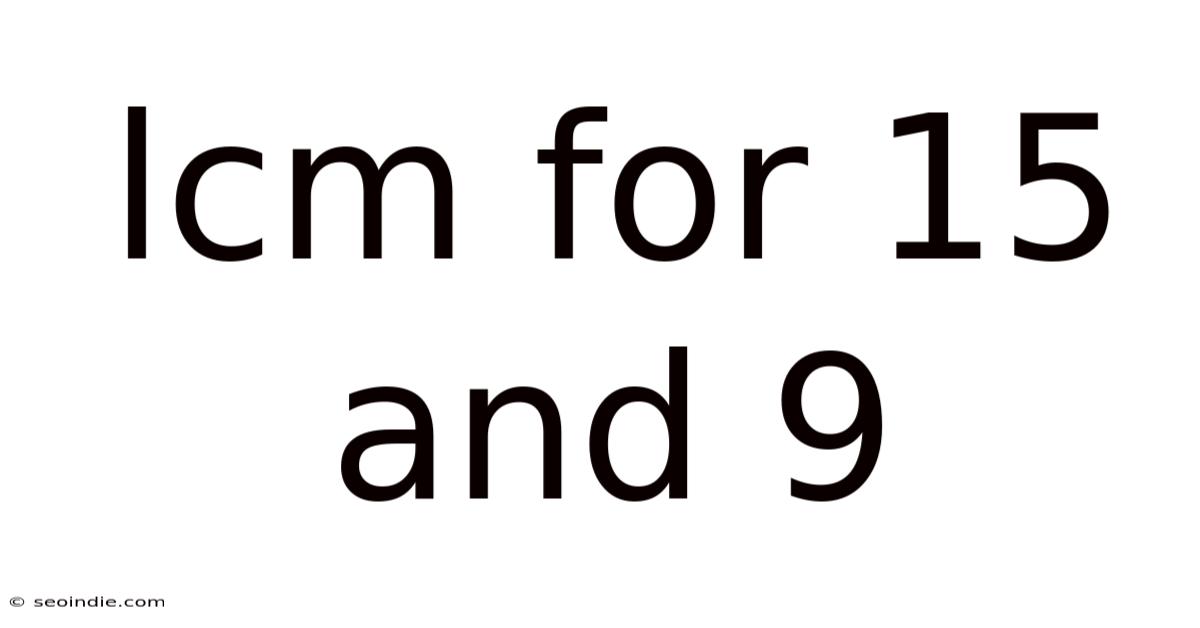
Table of Contents
Finding the LCM of 15 and 9: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications from simple fraction addition to complex scheduling problems. This comprehensive guide will explore how to find the LCM of 15 and 9, using several methods, explaining the underlying principles, and providing a deeper understanding of the concept for students of all levels. We'll delve into the different approaches, clarifying the rationale behind each step and addressing frequently asked questions.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 15 and 9, let's establish a solid understanding of what the LCM actually represents. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For example, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20…
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21…
The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple is 6.
Method 1: Listing Multiples
The simplest method, especially for smaller numbers like 15 and 9, is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105…
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99…
By comparing the lists, we can see that the smallest number appearing in both lists is 45. Therefore, the LCM of 15 and 9 is 45. This method is straightforward but becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
This method is more systematic and works well for larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime Factorization of 15: 15 = 3 x 5
- Prime Factorization of 9: 9 = 3 x 3 = 3²
Now, to find the LCM, we take the highest power of each prime factor present in either factorization:
- The highest power of 3 is 3² = 9
- The highest power of 5 is 5¹ = 5
Multiply these highest powers together: 9 x 5 = 45. Therefore, the LCM of 15 and 9 is 45. This method provides a more robust and efficient approach, particularly for larger numbers where listing multiples becomes impractical.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of two numbers are related through a simple formula:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
-
Finding the GCD of 15 and 9: We can use the Euclidean algorithm to find the GCD.
- 15 = 1 x 9 + 6
- 9 = 1 x 6 + 3
- 6 = 2 x 3 + 0
The last non-zero remainder is 3, so the GCD of 15 and 9 is 3.
-
Applying the formula:
LCM(15, 9) x GCD(15, 9) = 15 x 9 LCM(15, 9) x 3 = 135 LCM(15, 9) = 135 / 3 = 45
Therefore, the LCM of 15 and 9 is 45. This method is particularly useful when dealing with larger numbers where prime factorization might be more time-consuming.
Method 4: The Formula for Two Numbers
There's a direct formula that can be used for calculating the LCM of two numbers, a and b:
LCM(a, b) = (|a * b|) / GCD(a, b)
Where |a * b| represents the absolute value of the product of a and b, and GCD(a,b) is the greatest common divisor of a and b.
Using this for 15 and 9, we first find the GCD which is 3 (as calculated before). Then:
LCM(15, 9) = (|15 * 9|) / 3 = 135 / 3 = 45
This confirms, once again, that the LCM of 15 and 9 is 45.
Real-World Applications of LCM
Understanding LCM has practical applications in various scenarios:
-
Scheduling: Imagine two buses depart from the same stop, one every 15 minutes and the other every 9 minutes. The LCM (45 minutes) tells you when both buses will depart simultaneously again.
-
Fraction Addition: To add fractions with different denominators, you need to find the LCM of the denominators to create a common denominator.
-
Project Management: In project management, finding the LCM of different task durations can help in scheduling and resource allocation.
-
Music: In music theory, LCM is used to find the least common multiple of the durations of notes.
Explanation of the Mathematical Principles
The methods described above rely on fundamental number theory concepts:
-
Prime Factorization: Every positive integer greater than 1 can be uniquely represented as a product of prime numbers. This uniqueness is the cornerstone of the prime factorization method for finding LCM.
-
Euclidean Algorithm: This algorithm efficiently finds the GCD of two numbers, which is crucial for the GCD-based method and the formula-based method for LCM calculation.
-
Distributive Property: The relationship between LCM and GCD relies on the distributive property of multiplication over addition.
Frequently Asked Questions (FAQ)
Q1: Is there only one LCM for two numbers?
A1: Yes, there is only one least common multiple for any two given numbers.
Q2: What if the numbers are very large?
A2: For very large numbers, the prime factorization method might be computationally expensive. In such cases, more efficient algorithms for finding GCD (like the Euclidean algorithm) and subsequently the LCM are preferred.
Q3: Can we find the LCM of more than two numbers?
A3: Yes, you can extend these methods to find the LCM of more than two numbers. For prime factorization, you'd consider the highest power of each prime factor present in the factorization of any of the numbers. For the GCD method, you'd need to iteratively find the GCD of pairs of numbers and then use the formula.
Conclusion
Finding the LCM of 15 and 9, as demonstrated through various methods, highlights the fundamental concepts of number theory and their practical applications. While the listing multiples method is intuitive for small numbers, the prime factorization and GCD methods offer more efficient and robust approaches for larger numbers. Understanding these concepts is critical for success in mathematics and its applications in various fields. The LCM, seemingly a simple concept, underpins many complex calculations and real-world problems, showcasing the power of mathematical principles. Mastering the calculation of LCM will not only improve your mathematical skills but also provide a valuable tool for solving problems across different disciplines.
Latest Posts
Latest Posts
-
1 Liter Is 1000 Ml
Sep 21, 2025
-
Words That Start With Sn
Sep 21, 2025
-
Can A Probability Be Negative
Sep 21, 2025
-
What Animals Are A Herbivore
Sep 21, 2025
-
One Hundred And Forty One
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Lcm For 15 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.