Lcm 6 8 And 12
seoindie
Sep 16, 2025 · 6 min read
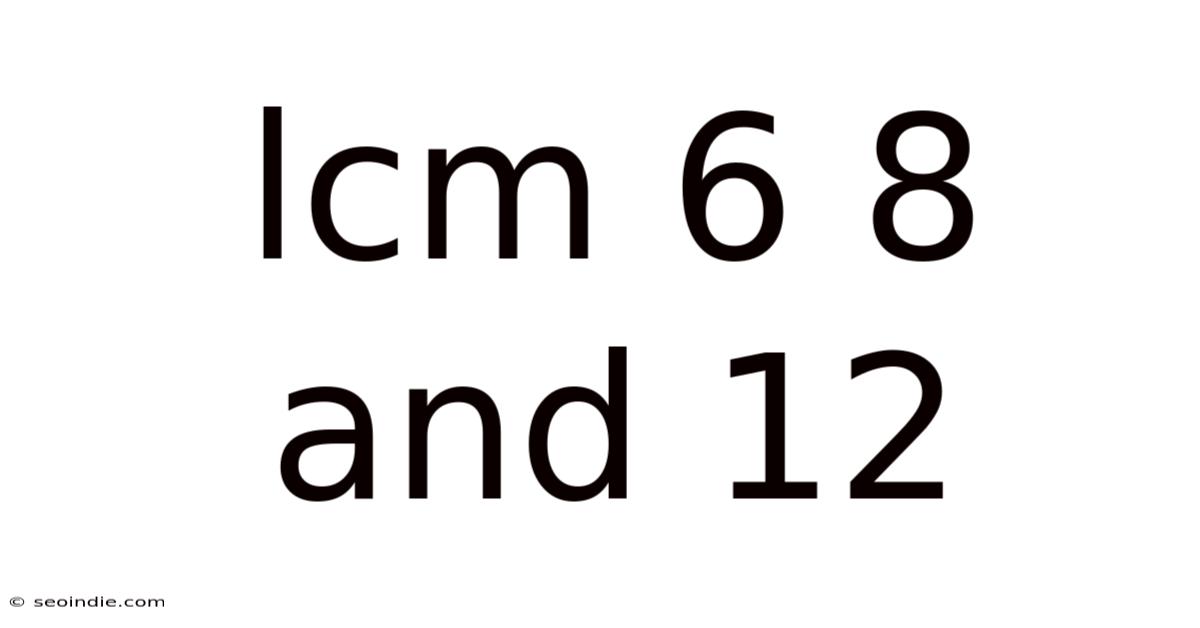
Table of Contents
Finding the LCM of 6, 8, and 12: A Comprehensive Guide
Finding the least common multiple (LCM) of numbers is a fundamental concept in mathematics, crucial for various applications ranging from simple fraction operations to complex scheduling problems. This comprehensive guide will walk you through understanding and calculating the LCM of 6, 8, and 12, explaining the underlying principles and providing multiple methods to solve this problem. We'll explore different approaches, ensuring you grasp not only the answer but also the why behind the calculations.
Understanding Least Common Multiple (LCM)
Before diving into the specifics of finding the LCM of 6, 8, and 12, let's clarify the definition. The least common multiple (LCM) of two or more numbers is the smallest positive integer that is a multiple of all the given numbers. In simpler terms, it's the smallest number that all the numbers you're considering can divide into evenly without leaving a remainder.
For example, the multiples of 6 are 6, 12, 18, 24, 30, 36, and so on. The multiples of 8 are 8, 16, 24, 32, 40, and so on. The multiples of 12 are 12, 24, 36, 48, and so on. Notice that 24 appears in all three lists. It's a common multiple. However, 24 is not the least common multiple; there are smaller common multiples. The smallest number that appears in all three lists is 24. Therefore, the LCM of 6, 8, and 12 is 24.
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three:
- Multiples of 6: 6, 12, 18, 24, 30, 36...
- Multiples of 8: 8, 16, 24, 32, 40...
- Multiples of 12: 12, 24, 36, 48...
The smallest number that appears in all three lists is 24. Therefore, the LCM(6, 8, 12) = 24.
While this method is simple for smaller numbers, it becomes less efficient as the numbers increase in size. Finding the LCM of larger numbers using this method would be time-consuming and prone to errors.
Method 2: Prime Factorization
This is a more efficient and systematic method, particularly useful for larger numbers. It involves expressing each number as a product of its prime factors.
-
Prime Factorization:
- 6 = 2 x 3
- 8 = 2 x 2 x 2 = 2³
- 12 = 2 x 2 x 3 = 2² x 3
-
Identifying the Highest Power of Each Prime Factor: Looking at the prime factorization of each number, we identify the highest power of each prime factor present:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
-
Multiplying the Highest Powers: To find the LCM, we multiply these highest powers together: LCM(6, 8, 12) = 2³ x 3 = 8 x 3 = 24
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers or a greater number of numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula connecting them:
LCM(a, b) * GCD(a, b) = a * b
While this formula is generally used for two numbers, we can extend the concept to three numbers by finding the LCM of two numbers first and then applying the formula again.
-
Find the GCD of 6, 8, and 12: We'll use the Euclidean algorithm to find the GCD:
- GCD(6, 8) = 2
- GCD(2, 12) = 2 Therefore, GCD(6,8,12) = 2
-
Apply the formula incrementally: Let's first find the LCM of 6 and 8: LCM(6,8) * GCD(6,8) = 6 * 8 LCM(6,8) * 2 = 48 LCM(6,8) = 24
Now, find the LCM of 24 and 12 using the same method: LCM(24,12) * GCD(24,12) = 24 * 12 LCM(24,12) * 12 = 288 LCM(24,12) = 24
Therefore, LCM(6, 8, 12) = 24.
This method is also robust, but the incremental application of the GCD-LCM relationship can be slightly more complex than the prime factorization method, especially when dealing with a large number of inputs.
Method 4: Using the Ladder Method (or Prime Factor Tree Method)
This method visually represents the prime factorization process, making it easier to track the highest powers of each prime factor.
- Arrange the Numbers: Write the numbers in a row.
- Divide by a Common Prime Factor: Find the smallest prime number that divides at least one of the numbers. Divide those numbers that are divisible and bring down the others.
- Repeat: Repeat step 2 until you only have 1's left.
- Multiply the Divisors: The LCM is the product of all the prime divisors used.
Let's see it in action for 6, 8, and 12:
2 | 6 8 12
2 | 3 4 6
2 | 3 2 3
3 | 3 1 3
| 1 1 1
The prime divisors are 2, 2, 2, and 3. Multiplying these together: 2 x 2 x 2 x 3 = 24. Therefore, LCM(6, 8, 12) = 24
Real-World Applications of LCM
Understanding and calculating LCM has practical applications in various situations:
- Scheduling: Imagine you have three different machines that complete a cycle in 6, 8, and 12 hours respectively. The LCM (24) tells you when all three machines will complete a cycle simultaneously again.
- Fractions: Finding the LCM of the denominators is crucial when adding or subtracting fractions.
- Measurement Conversions: Converting between different units of measurement often involves finding the LCM of the denominators.
- Project Planning: In project management, the LCM can help determine the optimal time to synchronize various tasks.
Frequently Asked Questions (FAQ)
-
What is the difference between LCM and GCD? The LCM is the smallest common multiple, while the GCD is the greatest common divisor. They are inversely related; a higher GCD implies a lower LCM and vice-versa.
-
Can I use a calculator to find the LCM? Many scientific calculators have built-in functions to calculate the LCM of numbers.
-
What if I have more than three numbers? The methods described above, particularly prime factorization, can be easily extended to find the LCM of more than three numbers. Simply find the highest power of each prime factor present in the factorization of all the numbers and multiply them together.
-
Why is the prime factorization method preferred for larger numbers? The prime factorization method is more efficient because it avoids the potentially lengthy process of listing multiples, which becomes impractical for larger numbers. It directly identifies the essential factors contributing to the LCM.
-
Is there only one LCM for a set of numbers? Yes, there is only one least common multiple for any given set of numbers.
Conclusion
Finding the least common multiple (LCM) is a valuable skill with broad applications in mathematics and beyond. This article explored four different methods to calculate the LCM of 6, 8, and 12, highlighting their strengths and weaknesses. While the listing multiples method is intuitive for small numbers, the prime factorization method emerges as the most efficient and versatile approach, especially when dealing with larger numbers. Mastering these techniques will empower you to confidently tackle LCM problems in various contexts and strengthen your understanding of fundamental mathematical concepts. Remember to choose the method that best suits your needs and the complexity of the numbers involved. The key takeaway is not just the answer (24), but the understanding of the underlying mathematical principles and the ability to apply these methods to a wider range of problems.
Latest Posts
Latest Posts
-
Area Of A Parallelogram Questions
Sep 16, 2025
-
Single Circulation And Double Circulation
Sep 16, 2025
-
Difference Of Rational Expressions Calculator
Sep 16, 2025
-
Words With The Suffix Ed
Sep 16, 2025
-
One Hundred And Eighty One
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm 6 8 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.