Is 50 A Square Number
seoindie
Sep 18, 2025 · 5 min read
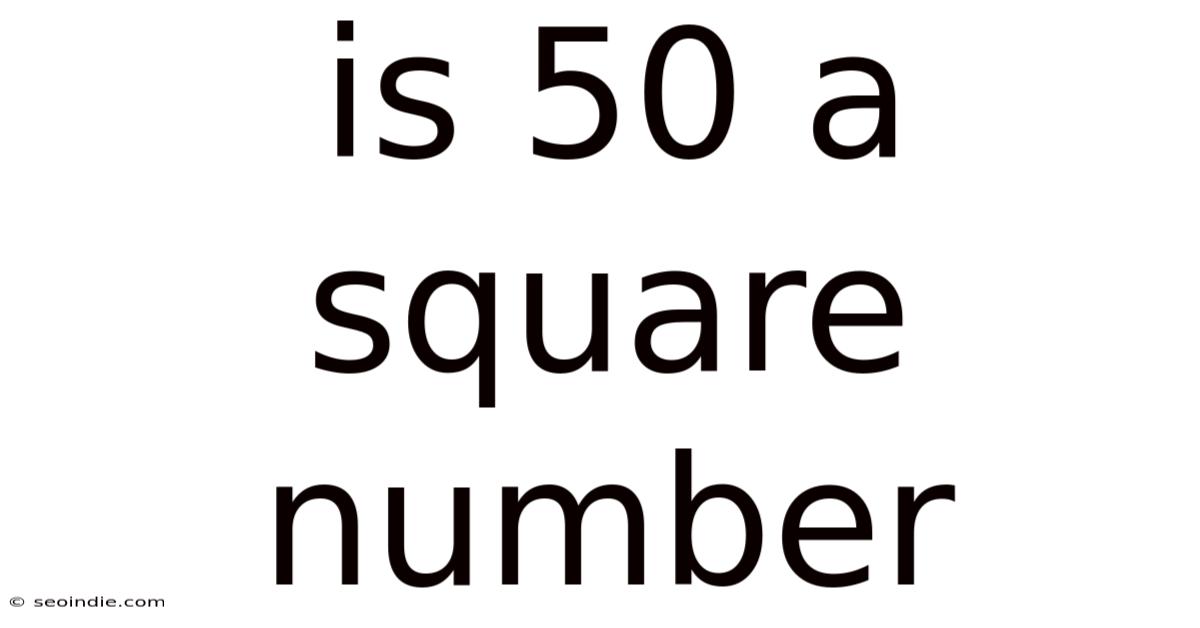
Table of Contents
Is 50 a Square Number? Unraveling the Mystery of Perfect Squares
Is 50 a square number? This seemingly simple question opens the door to a fascinating exploration of perfect squares, their properties, and how to determine whether a given number belongs to this exclusive club. This article will delve into the concept of square numbers, provide a definitive answer to the question about 50, and explore related mathematical concepts to deepen your understanding. We'll also address common misconceptions and answer frequently asked questions.
Understanding Square Numbers
A square number, also known as a perfect square, is a number that can be obtained by squaring (multiplying by itself) a whole number. In other words, it's the result of multiplying an integer by itself. For example:
- 1 x 1 = 1 (1 is a square number)
- 2 x 2 = 4 (4 is a square number)
- 3 x 3 = 9 (9 is a square number)
- 4 x 4 = 16 (16 is a square number)
- and so on...
These numbers (1, 4, 9, 16, etc.) are all perfect squares because they are the product of an integer multiplied by itself. The process of finding the square of a number is denoted using a superscript '2', for example, 5² = 5 x 5 = 25.
The Case of 50: Is it a Perfect Square?
Now, let's get to the core question: Is 50 a square number? The answer is no. There is no whole number that, when multiplied by itself, results in 50.
Let's consider the closest square numbers to 50:
- 7 x 7 = 49
- 8 x 8 = 64
As you can see, 50 falls between these two perfect squares. It's slightly larger than 49 (7²) and slightly smaller than 64 (8²). This conclusively demonstrates that 50 cannot be expressed as the square of an integer, therefore it is not a perfect square.
Exploring the Properties of Square Numbers
Understanding the properties of square numbers can help us more easily identify them. Some key characteristics include:
- Even Square Numbers: All even square numbers are divisible by 4. This is because an even number can be represented as 2n, and its square is (2n)² = 4n².
- Odd Square Numbers: All odd square numbers leave a remainder of 1 when divided by 8.
- Last Digit Pattern: The last digit of a perfect square can only be 0, 1, 4, 5, 6, or 9. This property is useful for quickly eliminating numbers as potential perfect squares. For instance, a number ending in 2, 3, 7, or 8 cannot be a perfect square.
- Sum of Odd Numbers: Each perfect square can be expressed as the sum of consecutive odd numbers starting from 1. For example:
- 1 = 1
- 4 = 1 + 3
- 9 = 1 + 3 + 5
- 16 = 1 + 3 + 5 + 7
- and so on...
- Geometric Representation: Perfect squares can be visually represented as square arrays of dots or objects. For example, the square number 9 can be arranged as a 3x3 grid.
Finding the Square Root: A Deeper Dive
Determining if a number is a perfect square often involves finding its square root. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 25 is 5 because 5 x 5 = 25.
Finding the square root of 50 will not yield a whole number. The square root of 50 is approximately 7.071, which confirms that 50 is not a perfect square because its square root is not an integer. Calculators and mathematical software can easily compute square roots, providing a quick way to check if a number is a perfect square.
Practical Applications of Square Numbers
The concept of square numbers isn't confined to theoretical mathematics; it has practical applications in various fields:
- Geometry: Calculating areas of squares and other geometric shapes frequently involves square numbers.
- Physics: Many physical phenomena, such as the trajectory of projectiles, involve calculations with squares and square roots.
- Computer Science: Square numbers are used in algorithms and data structures.
- Construction and Engineering: Square numbers are crucial in designing structures and calculating dimensions.
Common Misconceptions about Square Numbers
Some common misconceptions surrounding square numbers include:
- Confusing square numbers with square roots: While related, they are distinct concepts. The square of a number is the result of multiplying it by itself, while the square root is the number that, when multiplied by itself, gives the original number.
- Assuming all even numbers are square numbers: This is incorrect; many even numbers are not perfect squares.
- Misinterpreting decimal results: Getting a decimal result when attempting to find the square root of a number is a clear indication that it is not a perfect square.
Frequently Asked Questions (FAQ)
Q: How can I quickly determine if a large number is a perfect square?
A: While there's no single shortcut for extremely large numbers, checking the last digit and using estimation based on the closest perfect squares can often help eliminate possibilities. Calculators and computer programs offer the most efficient method for large numbers.
Q: Are there any patterns in the sequence of square numbers?
A: Yes, as discussed earlier, there are patterns related to their divisibility by 4 and 8, the last digit, and their representation as sums of consecutive odd numbers.
Q: What is the difference between a perfect square and a square root?
A: A perfect square is the result of squaring a whole number (e.g., 25 is a perfect square because 5² = 25). The square root is the number that, when squared, gives the original number (e.g., the square root of 25 is 5).
Q: Can negative numbers be square numbers?
A: No, in the context of real numbers, a perfect square is always a non-negative number because the product of two identical numbers (even if negative) always results in a positive number. The concept of square numbers with negative results requires delving into complex numbers which is beyond the scope of this article.
Conclusion
In conclusion, 50 is definitively not a square number. Understanding the concept of square numbers involves recognizing their properties, being able to identify them, and calculating square roots. This knowledge has applications across multiple disciplines, highlighting the importance of this seemingly simple mathematical concept. We hope this in-depth exploration has clarified the concept of perfect squares and provided a solid foundation for further mathematical exploration.
Latest Posts
Latest Posts
-
Convert Liters To Cubic Feet
Sep 18, 2025
-
3 Root 3 Whole Square
Sep 18, 2025
-
Is 43 A Composite Number
Sep 18, 2025
-
3 10 As A Decimal
Sep 18, 2025
-
Rank Of A Matrix Calculator
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Is 50 A Square Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.