Is 3/2 Greater Than 1
seoindie
Sep 13, 2025 · 6 min read
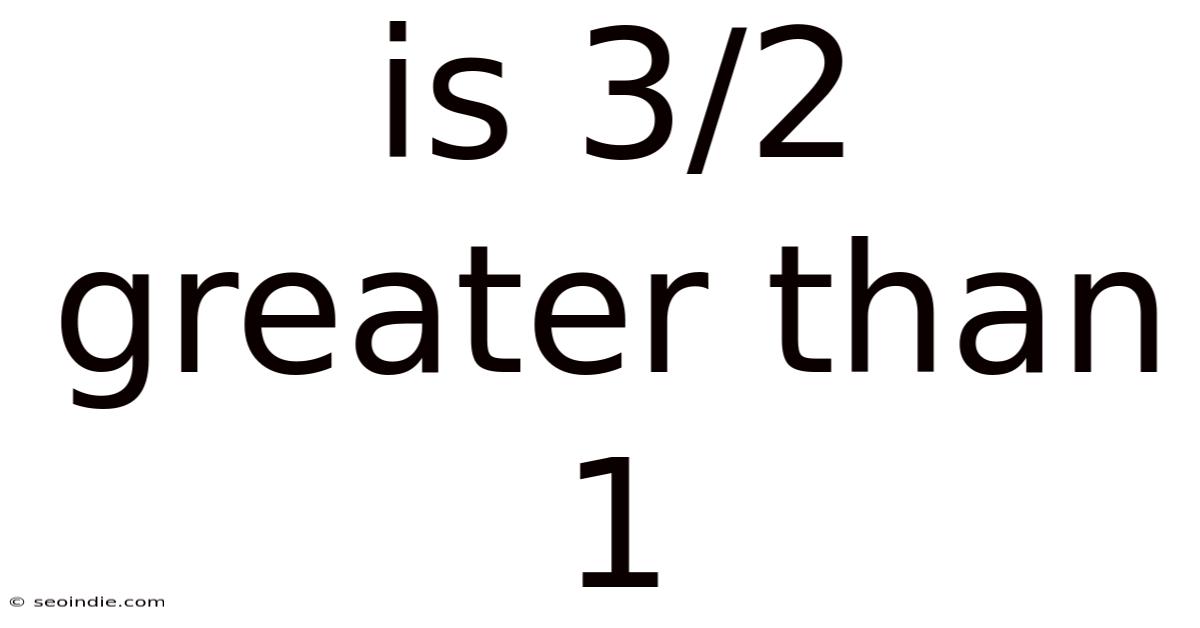
Table of Contents
Is 3/2 Greater Than 1? A Deep Dive into Fractions and Comparisons
Is 3/2 greater than 1? This seemingly simple question opens the door to a deeper understanding of fractions, their representation, and how to effectively compare them. While the answer might be immediately apparent to some, exploring the "why" behind the answer builds a strong foundation in mathematical reasoning, crucial for more advanced concepts. This article will not only answer the question definitively but will also explore various methods of comparing fractions, offering a comprehensive understanding of this fundamental mathematical principle.
Understanding Fractions: The Building Blocks
Before diving into the comparison, let's establish a solid understanding of what a fraction represents. A fraction, such as 3/2, expresses a part of a whole. The number on the top, the numerator, indicates the number of parts we have. The number on the bottom, the denominator, represents the total number of equal parts the whole is divided into.
In our example, 3/2, the numerator is 3 and the denominator is 2. This means we have 3 parts out of a total of 2 equal parts. This might seem counterintuitive at first – how can we have 3 parts when there are only 2 parts in total? This is where the concept of improper fractions comes into play.
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. Improper fractions represent values greater than or equal to 1. Proper fractions, on the other hand, have a numerator smaller than the denominator, representing values less than 1.
Visualizing 3/2: A Pictorial Representation
To grasp the concept visually, imagine a pizza cut into two equal slices. The fraction 3/2 represents having three of these slices. Since we only started with two slices, this means we have more than one whole pizza; we have one whole pizza and one extra half.
Comparing Fractions: Multiple Approaches
There are several ways to determine if 3/2 is greater than 1. Let's explore a few:
1. Converting to a Mixed Number:
An improper fraction can be converted into a mixed number, which combines a whole number and a proper fraction. To do this, we divide the numerator (3) by the denominator (2).
3 ÷ 2 = 1 with a remainder of 1.
This means 3/2 can be written as 1 1/2 (one and a half). Since 1 1/2 is clearly greater than 1, we can definitively say that 3/2 is greater than 1.
2. Converting to a Decimal:
Another approach is to convert the fraction into a decimal. We simply divide the numerator by the denominator:
3 ÷ 2 = 1.5
Since 1.5 is greater than 1, we again confirm that 3/2 is greater than 1. This method is particularly useful when comparing fractions with different denominators, as converting to decimals allows for easier comparison.
3. Using a Common Denominator:
If we were comparing 3/2 to another fraction, say 5/4, we could use the method of finding a common denominator. This involves finding a common multiple of the denominators. In this case, a common denominator for 2 and 4 is 4.
We would rewrite 3/2 with a denominator of 4:
3/2 = (3 x 2) / (2 x 2) = 6/4
Now, comparing 6/4 to 1 (which can be written as 4/4), it's clear that 6/4 is greater. This method is especially helpful when dealing with fractions that are not easily converted to decimals or mixed numbers.
4. Visual Comparison on a Number Line:
Placing 3/2 on a number line provides a clear visual representation. A number line shows numbers in order, and we can easily see that 3/2 (or 1.5) falls to the right of 1, indicating it is greater.
The Importance of Understanding Fraction Comparisons
The ability to compare fractions is a fundamental skill in mathematics. It's not just about determining which fraction is larger; it's about understanding the underlying concepts of ratios, proportions, and relative magnitudes. This understanding is crucial for success in various areas, including:
- Algebra: Solving equations and inequalities often involves manipulating fractions.
- Geometry: Calculating areas, volumes, and proportions of shapes frequently involves fraction comparisons.
- Data Analysis: Understanding proportions and percentages, which are closely related to fractions, is essential for interpreting data.
- Real-world applications: From baking and cooking (measuring ingredients) to managing finances (understanding percentages and proportions), fraction comparisons are used extensively in everyday life.
Addressing Common Misconceptions
Several misconceptions can arise when working with fractions. Let's address some common ones:
- Focusing solely on numerators: Some individuals might mistakenly believe that a larger numerator automatically means a larger fraction. This is only true if the denominators are the same. For instance, 3/4 is smaller than 5/4, even though 5 is larger than 3.
- Difficulty with improper fractions: The concept of improper fractions can be confusing at first. Remember that improper fractions represent values greater than or equal to 1.
- Lack of visual representation: Using visual aids like pizza slices or number lines can significantly improve understanding, especially for those who struggle with abstract concepts.
Frequently Asked Questions (FAQs)
Q: How can I quickly determine if a fraction is greater than 1?
A: A simple way is to compare the numerator and denominator. If the numerator is larger than the denominator, the fraction is greater than 1.
Q: What if I'm comparing fractions with different denominators?
A: Find a common denominator or convert the fractions to decimals for easier comparison.
Q: Are there any other methods for comparing fractions besides the ones mentioned?
A: Yes, you can also use cross-multiplication. For example, to compare 3/2 and 5/4, you would cross-multiply: (3 x 4) and (2 x 5). The larger product corresponds to the larger fraction. (12 > 10, therefore 3/2 > 5/4)
Q: Why is understanding fraction comparison important in real-world scenarios?
A: It's crucial for accurate measurements, calculating proportions, understanding percentages, and making informed decisions in various situations.
Conclusion: More Than Just a Simple Answer
The answer to the question, "Is 3/2 greater than 1?" is a resounding yes. However, this article aimed to go beyond the simple answer, exploring the underlying concepts of fractions, providing multiple methods for comparison, addressing common misconceptions, and highlighting the real-world importance of this fundamental mathematical skill. Mastering fraction comparison is not just about solving math problems; it's about developing a deeper understanding of numerical relationships and building a solid foundation for more advanced mathematical concepts. By employing the techniques discussed here, you can confidently tackle fraction comparisons and apply your knowledge to various fields.
Latest Posts
Latest Posts
-
Convert 10 30 Kilocalories To Joules
Sep 13, 2025
-
What Words Start With Aq
Sep 13, 2025
-
161cm To Inches And Feet
Sep 13, 2025
-
Zener Diode As Voltage Regulator
Sep 13, 2025
-
Words That Describe Your Dad
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Is 3/2 Greater Than 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.