Is 256 A Perfect Square
seoindie
Sep 11, 2025 · 6 min read
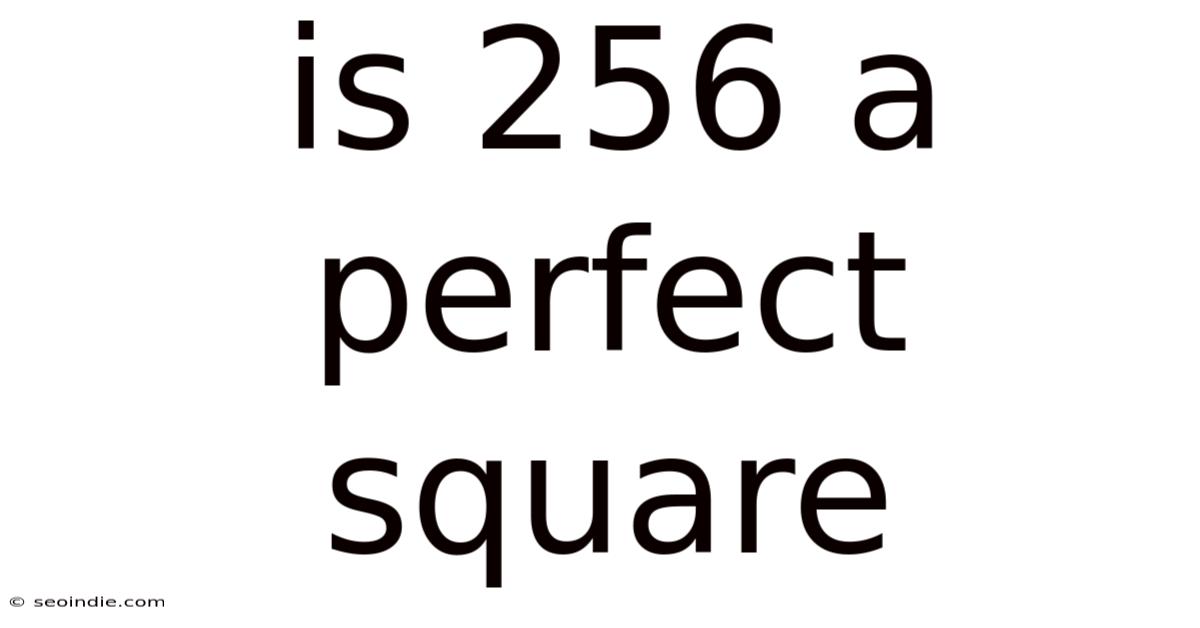
Table of Contents
Is 256 a Perfect Square? Unraveling the Mystery of Perfect Squares and Square Roots
Is 256 a perfect square? This seemingly simple question opens a door to a fascinating world of mathematics, exploring the concepts of perfect squares, square roots, and their significance in various fields. This comprehensive guide will not only answer this question definitively but also delve into the underlying principles, provide practical examples, and equip you with the tools to identify perfect squares independently. We'll also explore the historical context and applications of these mathematical concepts.
Understanding Perfect Squares
A perfect square is a number that can be obtained by squaring (multiplying by itself) an integer. In simpler terms, it's the result of multiplying a whole number by itself. For example:
- 1 x 1 = 1 (1 is a perfect square)
- 2 x 2 = 4 (4 is a perfect square)
- 3 x 3 = 9 (9 is a perfect square)
- 4 x 4 = 16 (16 is a perfect square)
- and so on...
The sequence of perfect squares continues infinitely: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, and so on. Notice a pattern? The differences between consecutive perfect squares increase progressively (3, 5, 7, 9, 11, etc.). This pattern is directly related to the properties of odd numbers.
Calculating Square Roots
The square root of a number is the value that, when multiplied by itself, equals the original number. The square root of a perfect square is always an integer. For example:
- √1 = 1
- √4 = 2
- √9 = 3
- √16 = 4
- and so on...
Finding the square root is the inverse operation of squaring a number. If we want to determine if a number is a perfect square, we can calculate its square root. If the result is an integer, the original number is a perfect square.
Is 256 a Perfect Square? The Definitive Answer
Now, let's address the central question: Is 256 a perfect square? To determine this, we need to find its square root. You might already know the answer, but let's explore different methods to arrive at the solution:
Method 1: Trial and Error
We can start by trying different integers:
- 10 x 10 = 100 (too small)
- 15 x 15 = 225 (too small)
- 16 x 16 = 256 (bingo!)
Therefore, since 16 x 16 = 256, 256 is a perfect square.
Method 2: Prime Factorization
Prime factorization is a powerful technique in number theory. It involves breaking down a number into its prime factors (numbers divisible only by 1 and themselves). Let's factorize 256:
256 = 2 x 128 = 2 x 2 x 64 = 2 x 2 x 2 x 32 = 2 x 2 x 2 x 2 x 16 = 2 x 2 x 2 x 2 x 2 x 8 = 2 x 2 x 2 x 2 x 2 x 2 x 4 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 2<sup>8</sup>
Notice that we have eight factors of 2. Since a perfect square has an even number of each prime factor in its prime factorization, and 8 is an even number, 256 is a perfect square. In fact, √256 = 2<sup>8/2</sup> = 2<sup>4</sup> = 16.
Method 3: Using a Calculator
The simplest method is using a calculator with a square root function. Simply input √256, and the calculator will return 16, confirming that 256 is indeed a perfect square.
The Significance of Perfect Squares
Perfect squares aren't just a mathematical curiosity; they have practical applications in various fields:
-
Geometry: Calculating the area of squares and other geometrical shapes often involves perfect squares. For instance, a square with a side length of 16 units has an area of 256 square units.
-
Computer Science: In binary systems, powers of 2 (which include many perfect squares) are frequently used in data storage and memory allocation. 256, being 2<sup>8</sup>, is a significant number in computer science, representing 256 bytes (or one kilobyte).
-
Physics and Engineering: Many physical phenomena and engineering calculations involve squared terms, leading to the use of perfect squares in various formulas and models.
-
Number Theory: Perfect squares play a crucial role in advanced number theory, particularly in areas like Diophantine equations and quadratic residues.
Beyond 256: Identifying Other Perfect Squares
Now that you understand how to determine if a number is a perfect square, let's look at some strategies for identifying them more efficiently:
-
Recognizing common squares: Familiarize yourself with the squares of the first 20 integers (or more!). This will allow you to quickly identify many perfect squares.
-
Estimating: If you are unsure about a larger number, try to estimate its square root. For instance, if you are presented with the number 625, you might guess that its square root is around 25 (since 20²=400 and 30²=900). Checking 25² confirms that 625 is a perfect square.
-
Using the properties of perfect squares: Remember that the difference between consecutive perfect squares increases by consecutive odd numbers (3, 5, 7, 9, etc.).
Frequently Asked Questions (FAQ)
Q: Are all even numbers perfect squares?
A: No. While some even numbers are perfect squares (e.g., 4, 16, 36), many even numbers are not (e.g., 2, 6, 10).
Q: Are all odd numbers perfect squares?
A: No. Many odd numbers are not perfect squares (e.g., 3, 5, 7, 11). However, some odd numbers are perfect squares (e.g., 1, 9, 25, 49).
Q: How can I find the square root of a number that isn't a perfect square?
A: The square root of a non-perfect square is an irrational number – a number that cannot be expressed as a simple fraction. You can approximate the square root using a calculator or through numerical methods.
Q: What are some real-world applications of perfect squares beyond those mentioned?
A: Perfect squares are used in various areas, including cryptography (where modular arithmetic involving squares is crucial), financial mathematics (in calculating compound interest), and even in music theory (related to harmonic progressions and frequency ratios).
Conclusion
We've conclusively established that 256 is indeed a perfect square, as its square root is the integer 16. This exploration has taken us beyond a simple yes or no answer, delving into the fundamental concepts of perfect squares and square roots, their mathematical properties, and their widespread applications across diverse fields. Understanding perfect squares is a cornerstone of mathematical literacy, opening doors to more complex mathematical concepts and their practical relevance in the world around us. By grasping the methods presented here, you are now equipped to confidently identify perfect squares and appreciate their significance in various areas of study and application.
Latest Posts
Latest Posts
-
Number 15 In Roman Numerals
Sep 11, 2025
-
How Many Pounds Is 6kg
Sep 11, 2025
-
How Long Is Ten Yards
Sep 11, 2025
-
Reticular Connective Tissue Under Microscope
Sep 11, 2025
-
Describing Words Beginning With E
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Is 256 A Perfect Square . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.