Is 25 An Even Number
seoindie
Sep 11, 2025 · 6 min read
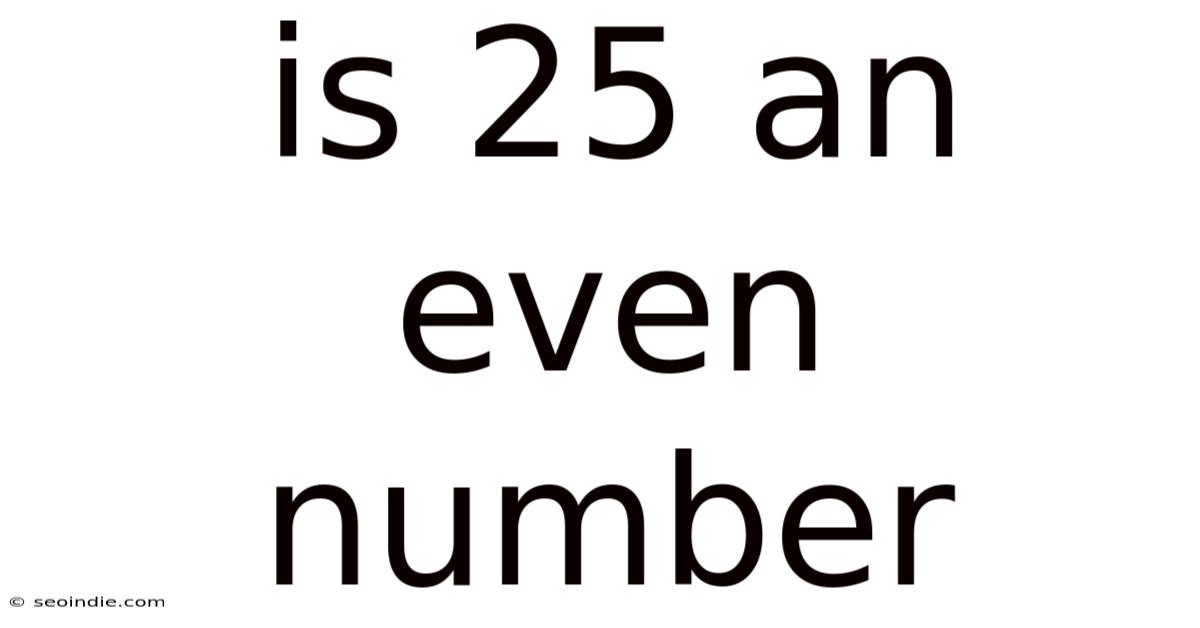
Table of Contents
Is 25 an Even Number? A Deep Dive into Even and Odd Numbers
Is 25 an even number? The simple answer is no. But understanding why 25 is not an even number requires delving into the fundamental concepts of even and odd numbers, their mathematical properties, and their applications in various fields. This comprehensive guide will not only answer the initial question but also equip you with a deeper understanding of number theory.
Introduction: Defining Even and Odd Numbers
Even and odd numbers are the two fundamental categories into which all integers (whole numbers) are classified. This seemingly simple classification has profound implications across mathematics and beyond. The distinction lies in their divisibility by 2.
-
Even numbers are integers that are perfectly divisible by 2, leaving no remainder. This means they can be expressed as 2n, where 'n' is any integer. Examples include 2, 4, 6, 8, 10, and so on.
-
Odd numbers are integers that are not perfectly divisible by 2. When divided by 2, they leave a remainder of 1. They can be expressed as 2n + 1, where 'n' is any integer. Examples include 1, 3, 5, 7, 9, and so on.
The number 25, when divided by 2, yields a quotient of 12 and a remainder of 1. This immediately shows that 25 is not divisible by 2 and therefore falls into the category of odd numbers.
Why the Even/Odd Distinction Matters
The seemingly simple distinction between even and odd numbers has significant implications across numerous areas of mathematics:
-
Modular Arithmetic: The concept of even and odd numbers forms the basis of modular arithmetic, particularly modulo 2. This is a system of arithmetic where numbers "wrap around" after reaching a certain value (in this case, 2). Even numbers are congruent to 0 (mod 2), and odd numbers are congruent to 1 (mod 2). This has applications in cryptography and computer science.
-
Number Theory: Even and odd numbers play a crucial role in various number theory theorems and proofs. For instance, the sum of two even numbers is always even, the sum of two odd numbers is always even, and the sum of an even and an odd number is always odd. These properties are fundamental to many more complex mathematical concepts.
-
Algebra: The parity (evenness or oddness) of numbers influences algebraic manipulations. Understanding the parity of variables can simplify equation solving and problem-solving in various algebraic contexts.
-
Combinatorics and Probability: The even/odd classification of numbers is useful in combinatorial problems, particularly when dealing with permutations and combinations. Understanding the parity can help simplify calculations and identify patterns.
-
Geometry: Even and odd numbers are relevant in certain geometric problems, particularly those involving symmetry and tessellations. For example, the number of sides in a polygon directly influences its properties and symmetry.
Exploring the Properties of Even and Odd Numbers
Let's delve deeper into the properties of even and odd numbers, reinforcing why 25 is definitively odd:
-
Addition and Subtraction:
- Even + Even = Even (e.g., 2 + 4 = 6)
- Odd + Odd = Even (e.g., 3 + 5 = 8)
- Even + Odd = Odd (e.g., 2 + 3 = 5)
- Even - Even = Even (e.g., 6 - 2 = 4)
- Odd - Odd = Even (e.g., 7 - 3 = 4)
- Even - Odd = Odd (e.g., 6 - 3 = 3)
- Odd - Even = Odd (e.g., 7 - 4 = 3)
-
Multiplication:
- Even × Even = Even (e.g., 2 × 4 = 8)
- Odd × Odd = Odd (e.g., 3 × 5 = 15)
- Even × Odd = Even (e.g., 2 × 3 = 6)
- Odd × Even = Even (e.g., 3 × 2 = 6)
These properties demonstrate the consistent behavior of even and odd numbers under basic arithmetic operations. Notice how 25, an odd number, consistently adheres to these rules when involved in calculations with even or odd numbers.
Visualizing Even and Odd Numbers
We can visualize even and odd numbers using simple representations. Imagine arranging objects (dots, pebbles, etc.) in pairs. Even numbers can be arranged into complete pairs, with no objects left over. Odd numbers always leave one object unpaired. For 25, you would have 12 pairs with one object remaining, visually demonstrating its odd nature.
Common Misconceptions about Even and Odd Numbers
Despite the simplicity of the concept, some misconceptions exist:
-
Confusion with decimal representation: The presence of a 5 in the ones place doesn't automatically make a number odd. Consider the number 150; while it ends in 5, it is still even due to its divisibility by 2.
-
Ignoring remainders: Correctly identifying even and odd numbers relies on examining the remainder after division by 2. Ignoring the remainder can lead to incorrect classification.
-
Assuming only integers: The concept of even and odd numbers strictly applies to integers. Fractions and decimals are neither even nor odd.
Advanced Concepts Related to Even and Odd Numbers
The concept of even and odd numbers extends into more advanced mathematical fields:
-
Fermat's Last Theorem: This celebrated theorem, which states that there are no whole number solutions to the equation xⁿ + yⁿ = zⁿ for any integer value of n greater than 2, indirectly relates to the properties of even and odd numbers in its proof.
-
Goldbach's Conjecture: This unproven conjecture suggests that every even number greater than 2 can be expressed as the sum of two prime numbers. The conjecture directly involves even numbers and their relationship to prime numbers.
-
Parity arguments in proofs: In many mathematical proofs, especially in combinatorics and graph theory, arguments based on the parity of numbers are used to establish the existence or non-existence of certain solutions or structures.
Frequently Asked Questions (FAQ)
-
Q: Is zero an even or odd number? A: Zero is considered an even number because it is divisible by 2 with a remainder of 0.
-
Q: Can negative numbers be even or odd? A: Yes. Negative integers can also be classified as even or odd based on their divisibility by 2. For example, -2, -4, -6 are even, while -1, -3, -5 are odd.
-
Q: Are there any practical applications of even and odd numbers outside mathematics? A: Yes, even and odd numbers have applications in various fields such as scheduling (even/odd days of the week), computer science (bit manipulation), and physics (quantum mechanics).
Conclusion:
25 is unequivocally an odd number because it is not perfectly divisible by 2; it leaves a remainder of 1. Understanding the distinction between even and odd numbers is crucial for foundational mathematical understanding and extends to various advanced topics. This exploration demonstrates not only the straightforward classification but also the significant implications of this seemingly simple concept across numerous mathematical and scientific fields. The properties of even and odd numbers, their inherent relationships, and their applications highlight the beauty and interconnectedness of mathematical concepts. From simple arithmetic to advanced theorems, the parity of a number often plays a critical, albeit sometimes subtle, role.
Latest Posts
Latest Posts
-
Diploid Cell Vs Haploid Cell
Sep 11, 2025
-
Glacial Acetic Acid Boiling Point
Sep 11, 2025
-
Words That Start With We
Sep 11, 2025
-
Words That Start With Bal
Sep 11, 2025
-
2 3 As A Mixed Number
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Is 25 An Even Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.