Is 24 A Perfect Square
seoindie
Sep 20, 2025 · 5 min read
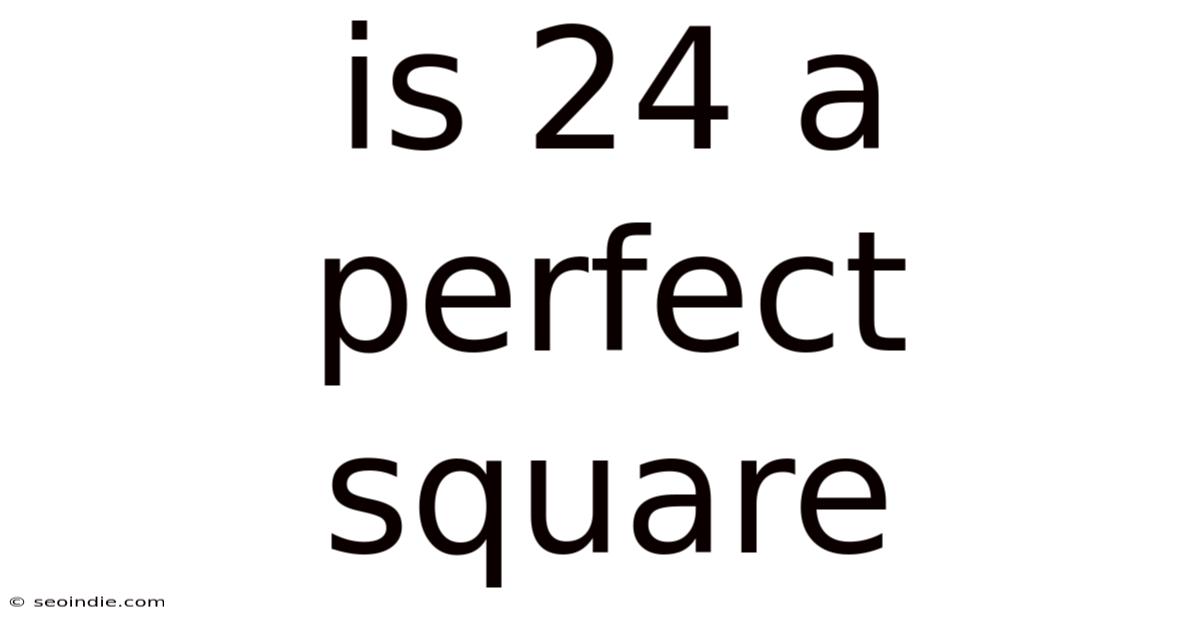
Table of Contents
Is 24 a Perfect Square? Unraveling the Mystery of Square Numbers
Is 24 a perfect square? This seemingly simple question opens the door to a deeper understanding of number theory and the fascinating world of perfect squares. While the answer itself is straightforward, exploring the why behind the answer provides a valuable learning experience in mathematical concepts. This article will not only definitively answer the question but also delve into the properties of perfect squares, explore different methods to identify them, and provide a solid foundation for further mathematical exploration.
Understanding Perfect Squares
A perfect square is a number that can be obtained by squaring (multiplying by itself) an integer. In simpler terms, it's the result of multiplying a whole number by itself. For example:
- 1 x 1 = 1 (1 is a perfect square)
- 2 x 2 = 4 (4 is a perfect square)
- 3 x 3 = 9 (9 is a perfect square)
- 4 x 4 = 16 (16 is a perfect square)
- 5 x 5 = 25 (25 is a perfect square)
And so on. Notice a pattern? Perfect squares are always positive integers, and they have specific characteristics we'll explore further.
Why 24 is Not a Perfect Square
The simple answer is no, 24 is not a perfect square. There is no integer that, when multiplied by itself, equals 24. Let's examine why:
-
Finding the Square Root: One way to determine if a number is a perfect square is to find its square root. The square root of a number is the value that, when multiplied by itself, gives the original number. The square root of 24 is approximately 4.898979... Since this is not a whole number, 24 is not a perfect square.
-
Prime Factorization: Another powerful technique involves prime factorization. Prime factorization breaks down a number into its prime factors – numbers that are only divisible by 1 and themselves. Let's find the prime factorization of 24:
24 = 2 x 12 = 2 x 2 x 6 = 2 x 2 x 2 x 3 = 2³ x 3¹
Perfect squares always have even exponents in their prime factorization. Notice that the exponent of 2 is 3 (odd) and the exponent of 3 is 1 (odd). Because the exponents are not even, 24 cannot be a perfect square.
-
Listing Perfect Squares: A more basic, albeit time-consuming, approach is to simply list the perfect squares until you either find 24 or surpass it. We already listed several above: 1, 4, 9, 16, 25, 36, 49, 64… As you can see, 24 doesn't appear in this list.
Properties of Perfect Squares
Understanding the properties of perfect squares allows for quicker identification and helps in solving various mathematical problems. Here are some key properties:
-
Even Exponents in Prime Factorization: As demonstrated earlier, the prime factorization of a perfect square will always have even exponents for all its prime factors.
-
Last Digit Pattern: The last digit of a perfect square can only be one of these digits: 0, 1, 4, 5, 6, 9. This property can be a quick way to eliminate possibilities when determining if a number is a perfect square. For instance, since 24 ends in 4, it could potentially be a perfect square, but further examination is necessary.
-
Square Root is an Integer: The square root of a perfect square will always be an integer.
-
Sum of Consecutive Odd Numbers: Every perfect square can be expressed as the sum of consecutive odd numbers. For example:
1 = 1 4 = 1 + 3 9 = 1 + 3 + 5 16 = 1 + 3 + 5 + 7 25 = 1 + 3 + 5 + 7 + 9
-
Geometric Representation: Perfect squares can be visually represented as squares. For example, the perfect square 16 can be represented as a 4x4 square. This visual representation can be helpful in understanding the concept.
Identifying Perfect Squares: Advanced Techniques
While the methods discussed above are sufficient for smaller numbers, more advanced techniques are necessary for larger numbers. These techniques often involve algorithms and programming, but understanding the underlying principles is crucial.
-
Newton-Raphson Method: This iterative method provides a highly efficient way to approximate the square root of a number. While it doesn't directly determine if a number is a perfect square, a non-integer result indicates that the number is not a perfect square.
-
Binary Search: This algorithm can efficiently search within a range of numbers to determine if a perfect square exists. It's particularly useful for larger numbers where manual checking is impractical.
Frequently Asked Questions (FAQ)
-
Q: What are some real-world applications of perfect squares?
A: Perfect squares appear frequently in various fields, including geometry (area calculations), physics (kinetic energy formulas), and computer science (algorithms).
-
Q: Are there any other numbers that aren't perfect squares?
A: Yes, the vast majority of numbers are not perfect squares. Any number that doesn't satisfy the conditions mentioned above (even exponents in prime factorization, integer square root, etc.) is not a perfect square.
-
Q: How can I learn more about number theory?
A: Numerous resources are available, including textbooks, online courses, and educational websites dedicated to mathematics. Exploring these resources will enhance your understanding of number theory and related concepts.
Conclusion
In conclusion, 24 is definitively not a perfect square. This article has explored various methods for determining whether a number is a perfect square, emphasizing the importance of prime factorization and the properties of perfect squares. Understanding these concepts is crucial not only for solving mathematical problems but also for appreciating the beauty and elegance of number theory. The seemingly simple question of whether 24 is a perfect square has provided a pathway to delve into a rich and fascinating area of mathematics, encouraging further exploration and discovery. The exploration of perfect squares extends far beyond simply identifying them; it lays the groundwork for a deeper understanding of mathematical principles and their applications in various fields. Remember, mathematics is a journey of discovery, and each question answered opens doors to new avenues of exploration.
Latest Posts
Latest Posts
-
Action Verbs Starting With E
Sep 20, 2025
-
Differentiate Between Solute And Solvent
Sep 20, 2025
-
How Do You Spell 2
Sep 20, 2025
-
100 Acres To Sq Miles
Sep 20, 2025
-
Is Dirt Abiotic Or Biotic
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Is 24 A Perfect Square . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.