Is 2/3 Bigger Than 1/2
seoindie
Sep 23, 2025 · 5 min read
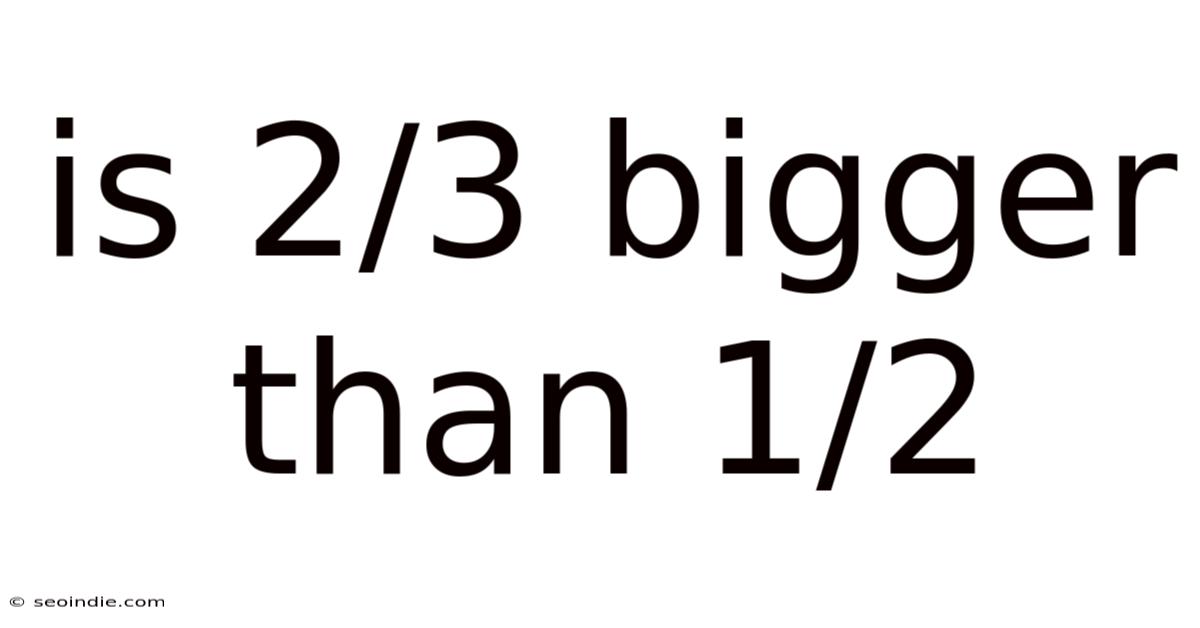
Table of Contents
Is 2/3 Bigger Than 1/2? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and advanced studies. This article delves into the question: Is 2/3 bigger than 1/2? We'll not only answer this question definitively but also explore various methods for comparing fractions, providing you with a solid understanding of the concept. This will equip you with the tools to compare any two fractions confidently.
Introduction: Understanding Fractions
A fraction represents a part of a whole. It's written as a ratio of two numbers: a numerator (top number) and a denominator (bottom number). The denominator shows the total number of equal parts the whole is divided into, and the numerator shows how many of those parts we're considering. For example, in the fraction 1/2, the denominator (2) indicates the whole is divided into two equal parts, and the numerator (1) indicates we're considering one of those parts.
Now, let's tackle our central question: Is 2/3 bigger than 1/2?
Method 1: Visual Comparison
The simplest way to compare fractions is through visual representation. Imagine two identical circles.
- For 1/2: Divide the first circle into two equal halves. Shade one half.
- For 2/3: Divide the second circle into three equal thirds. Shade two thirds.
By visually comparing the shaded portions, it's clear that the shaded area representing 2/3 is larger than the shaded area representing 1/2. Therefore, yes, 2/3 is bigger than 1/2.
This method is excellent for building intuition and understanding, particularly for beginners. However, it becomes less practical when dealing with more complex fractions.
Method 2: Finding a Common Denominator
This is a more robust and widely applicable method for comparing fractions. The key is to find a common denominator, which is a number that is a multiple of both denominators. For 2/3 and 1/2, the least common denominator (LCD) is 6 (because 6 is the smallest number divisible by both 3 and 2).
- Convert 2/3: To get a denominator of 6, we multiply both the numerator and denominator of 2/3 by 2: (2 * 2) / (3 * 2) = 4/6
- Convert 1/2: To get a denominator of 6, we multiply both the numerator and denominator of 1/2 by 3: (1 * 3) / (2 * 3) = 3/6
Now we compare 4/6 and 3/6. Since 4 > 3, we conclude that 4/6 > 3/6, meaning 2/3 > 1/2.
This method works for any pair of fractions, making it a reliable tool for comparison.
Method 3: Converting to Decimals
Another approach is to convert both fractions into decimals and then compare them.
- Convert 2/3: 2 divided by 3 is approximately 0.6667
- Convert 1/2: 1 divided by 2 is 0.5
Since 0.6667 > 0.5, we conclude that 2/3 > 1/2.
This method is straightforward and easily done with a calculator, making it a practical option, especially for larger or more complex fractions. However, remember that some fractions, like 2/3, result in repeating decimals, requiring rounding which might introduce minor inaccuracies.
Method 4: Cross-Multiplication
This is a quick and efficient method for comparing fractions. Cross-multiply the numerators and denominators:
- Multiply the numerator of the first fraction (2) by the denominator of the second fraction (2): 2 * 2 = 4
- Multiply the numerator of the second fraction (1) by the denominator of the first fraction (3): 1 * 3 = 3
Compare the results: 4 > 3. Since the result of the first multiplication is greater, the first fraction (2/3) is larger. Therefore, 2/3 > 1/2.
This method is particularly useful for quick comparisons, especially when dealing with larger numbers.
A Deeper Look: Understanding the Magnitude of the Difference
While we've established that 2/3 is larger than 1/2, it's also beneficial to understand how much larger. We can find the difference:
2/3 - 1/2 = (4/6) - (3/6) = 1/6
This means 2/3 is 1/6 larger than 1/2. This small difference highlights the importance of precise comparison methods when working with fractions.
Illustrative Examples: Applying Fraction Comparison
Let's apply these methods to a couple more examples:
Example 1: Is 3/4 bigger than 2/3?
Using the common denominator method (LCD = 12):
- 3/4 = 9/12
- 2/3 = 8/12
Since 9/12 > 8/12, 3/4 > 2/3.
Example 2: Is 5/8 bigger than 3/5?
Using cross-multiplication:
- 5 * 5 = 25
- 3 * 8 = 24
Since 25 > 24, 5/8 > 3/5.
Frequently Asked Questions (FAQ)
-
Q: Why is finding a common denominator important? A: Finding a common denominator allows us to compare fractions with different denominators by expressing them with the same denominator, making the comparison straightforward.
-
Q: Which method is the best? A: There's no single "best" method. The optimal approach depends on the complexity of the fractions and your personal preference. Visual comparison is excellent for building understanding, while cross-multiplication is efficient for quick comparisons. The common denominator method is reliable and universally applicable.
-
Q: What if the fractions have very large denominators? A: For fractions with very large denominators, using a calculator to convert to decimals or employing a computer program for fraction comparison might be more practical.
-
Q: Can I use a calculator to compare fractions? A: Yes, most calculators can handle fraction calculations and will directly display which fraction is larger.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental skill in mathematics. This article explored four different methods: visual comparison, finding a common denominator, converting to decimals, and cross-multiplication. Each method offers a unique approach to understanding and comparing fractions, allowing you to choose the most suitable method depending on the context and the complexity of the fractions involved. Mastering these methods empowers you to confidently tackle various mathematical problems and real-world scenarios involving fractions. Remember to choose the method you find most comfortable and efficient, and always double-check your work to ensure accuracy. The key is to understand the underlying principles and to practice regularly to build proficiency. With enough practice, comparing fractions will become second nature.
Latest Posts
Latest Posts
-
Projects Of The Solar System
Sep 24, 2025
-
What Roman Numeral Is 35
Sep 24, 2025
-
When To Use An Exclamation
Sep 24, 2025
-
Multiples Of 6 To 100
Sep 24, 2025
-
Is 77 Prime Or Composite
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 Bigger Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.