Is 15 Odd Or Even
seoindie
Sep 14, 2025 · 5 min read
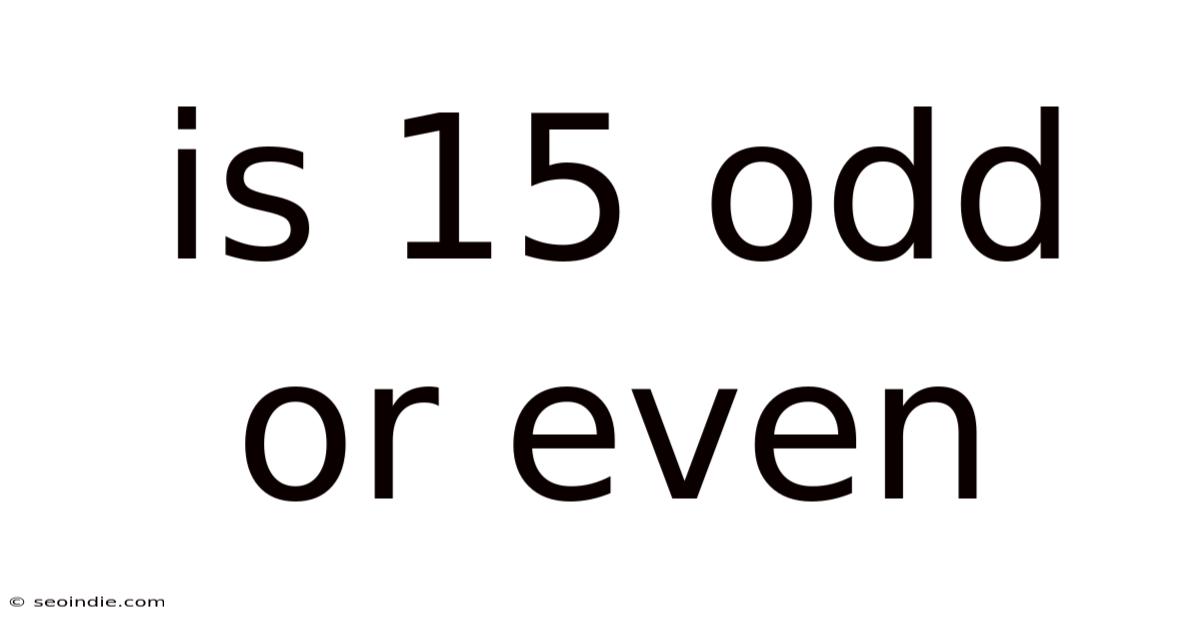
Table of Contents
Is 15 Odd or Even? A Deep Dive into Number Theory
Is 15 odd or even? This seemingly simple question opens the door to a fascinating exploration of number theory, a branch of mathematics dealing with the properties of integers. While the answer itself is straightforward, understanding why 15 is odd provides a foundation for grasping more complex mathematical concepts. This article will not only definitively answer the question but will also delve into the underlying principles, exploring related concepts and addressing common misconceptions. We'll also consider the practical applications of understanding odd and even numbers.
Understanding Odd and Even Numbers: The Basics
The classification of numbers as odd or even is based on their divisibility by 2. An even number is any integer that is perfectly divisible by 2, meaning it leaves no remainder when divided by 2. Examples include 2, 4, 6, 8, 10, and so on. Conversely, an odd number is any integer that is not perfectly divisible by 2; it leaves a remainder of 1 when divided by 2. Examples include 1, 3, 5, 7, 9, and 15.
So, to answer the initial question directly: 15 is an odd number. When you divide 15 by 2, you get 7 with a remainder of 1. This remainder is the key indicator that 15 belongs to the set of odd numbers.
Delving Deeper: Mathematical Properties of Odd and Even Numbers
The distinction between odd and even numbers leads to several interesting mathematical properties. Understanding these properties helps solidify our comprehension of the number system and provides a basis for more advanced mathematical explorations.
-
Addition and Subtraction:
- The sum of two even numbers is always even. (e.g., 2 + 4 = 6)
- The sum of two odd numbers is always even. (e.g., 3 + 5 = 8)
- The sum of an even number and an odd number is always odd. (e.g., 2 + 3 = 5)
- The difference between two even numbers is always even. (e.g., 6 - 2 = 4)
- The difference between two odd numbers is always even. (e.g., 7 - 3 = 4)
- The difference between an even number and an odd number is always odd. (e.g., 6 - 3 = 3)
-
Multiplication:
- The product of two even numbers is always even. (e.g., 2 x 4 = 8)
- The product of two odd numbers is always odd. (e.g., 3 x 5 = 15)
- The product of an even number and an odd number is always even. (e.g., 2 x 3 = 6)
-
Squares and Cubes:
- The square of an even number is always even. (e.g., 4² = 16)
- The square of an odd number is always odd. (e.g., 3² = 9)
- The cube of an even number is always even. (e.g., 2³ = 8)
- The cube of an odd number is always odd. (e.g., 3³ = 27)
These properties are not just abstract rules; they are fundamental to many mathematical proofs and algorithms. They form the bedrock upon which more complex concepts are built.
Beyond the Basics: Representing Odd and Even Numbers Algebraically
We can represent odd and even numbers algebraically, which provides a powerful tool for proving mathematical statements.
-
Even Numbers: Any even number can be represented as 2n, where 'n' is any integer. This is because any even number is a multiple of 2.
-
Odd Numbers: Any odd number can be represented as 2n + 1, where 'n' is any integer. This captures the fact that an odd number is one more than an even number.
Using this algebraic representation, we can easily prove the properties mentioned earlier. For example, let's prove that the sum of two odd numbers is always even:
Let one odd number be 2a + 1 and another odd number be 2b + 1, where 'a' and 'b' are integers. Their sum is:
(2a + 1) + (2b + 1) = 2a + 2b + 2 = 2(a + b + 1)
Since (a + b + 1) is an integer, the sum is a multiple of 2, and therefore, it's an even number. This algebraic approach provides a rigorous and generalizable proof.
Practical Applications: Where Odd and Even Numbers Matter
While the concept might seem purely theoretical, the distinction between odd and even numbers has practical applications across various fields:
-
Computer Science: Understanding odd and even numbers is crucial in algorithms related to bit manipulation, data structures, and cryptography. Parity checks, used to detect errors in data transmission, rely heavily on the properties of odd and even numbers.
-
Engineering: In engineering design, considerations of symmetry and balance often involve the use of even and odd numbers. For instance, in structural engineering, the placement of supports might be determined by even or odd number sequences for optimal stability.
-
Game Theory and Combinatorics: Many games and combinatorial problems involve counting techniques where understanding odd and even numbers simplifies calculations and helps in finding solutions.
-
Scheduling and Optimization: In scheduling problems, understanding odd and even numbers can assist in designing efficient and balanced schedules. For example, in resource allocation, assigning tasks based on odd or even numbers can optimize resource utilization.
Addressing Common Misconceptions
There are a few common misconceptions related to odd and even numbers that are worth addressing:
-
Zero is even: Many people mistakenly believe zero is odd. However, zero is perfectly divisible by 2, leaving no remainder, making it an even number.
-
Negative numbers: The concept of odd and even applies to negative integers as well. Negative even numbers are -2, -4, -6, etc., while negative odd numbers are -1, -3, -5, etc.
-
Fractions and decimals: The classification of odd and even applies only to integers (whole numbers). Fractions and decimals are neither odd nor even.
Conclusion: The Significance of a Simple Concept
The question "Is 15 odd or even?" might seem trivial, but exploring its answer unveils a rich landscape within number theory. Understanding the properties of odd and even numbers provides a foundation for grasping more complex mathematical ideas and has practical applications in various fields. From the simple act of dividing by 2 to the sophisticated use of algebraic representation, the concept of odd and even numbers showcases the elegance and power of mathematical principles, even in their most fundamental forms. The seemingly simple distinction between odd and even numbers proves to be surprisingly significant in the broader context of mathematics and its real-world applications. This exploration underscores the importance of digging beneath the surface of seemingly straightforward questions, revealing the wealth of knowledge that lies hidden just beneath the surface.
Latest Posts
Latest Posts
-
152cm To Feet And Inches
Sep 15, 2025
-
Difference Between Diploid And Haploid
Sep 15, 2025
-
Is Length Intensive Or Extensive
Sep 15, 2025
-
Words That Starts With Az
Sep 15, 2025
-
What Is Half Of 78
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Is 15 Odd Or Even . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.