Is 15 An Odd Number
seoindie
Sep 12, 2025 · 6 min read
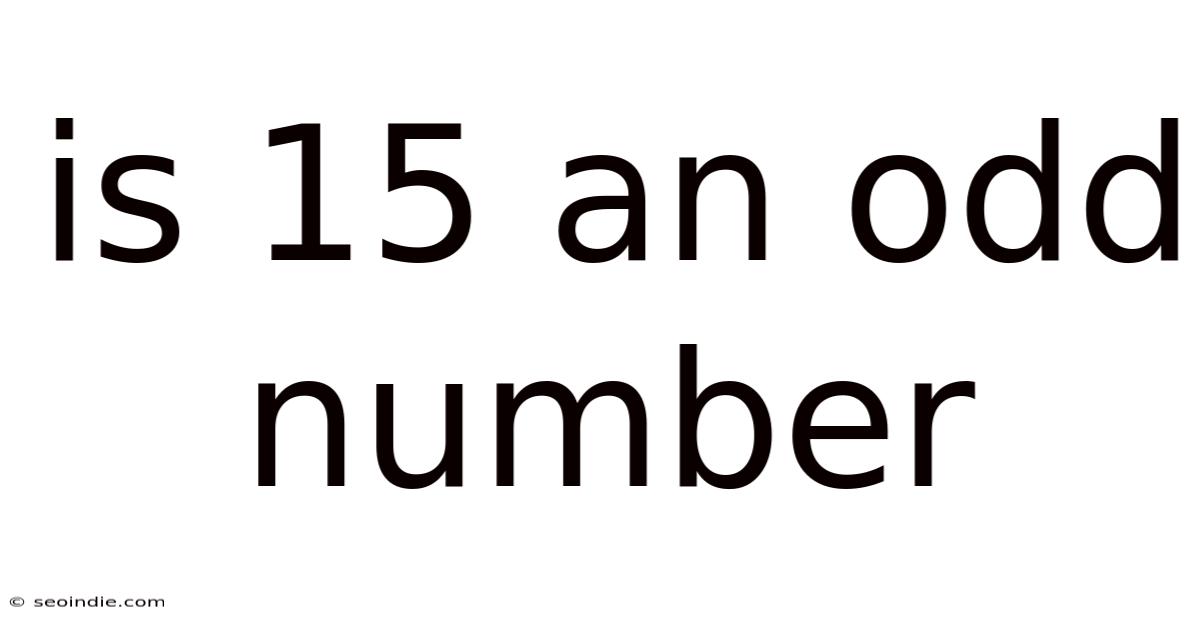
Table of Contents
Is 15 an Odd Number? A Deep Dive into Odd and Even Numbers
Is 15 an odd number? The answer, simply put, is yes. But this seemingly straightforward question opens a door to a fascinating exploration of number theory, encompassing definitions, properties, and practical applications of odd and even numbers. This article will delve into the intricacies of odd and even numbers, definitively answering the question regarding 15 and expanding your understanding of these fundamental mathematical concepts. We'll explore the underlying principles, look at how we identify odd and even numbers, and even touch upon some interesting historical context.
Understanding Odd and Even Numbers: The Basics
Before we definitively label 15, let's establish a solid understanding of what constitutes an odd and an even number. The core distinction lies in their divisibility by 2.
-
Even Numbers: An even number is any integer that is perfectly divisible by 2, leaving no remainder. This means it can be expressed as 2 * n, where 'n' is any integer (whole number). Examples include 2, 4, 6, 8, 10, and so on.
-
Odd Numbers: An odd number is any integer that is not perfectly divisible by 2. When divided by 2, it leaves a remainder of 1. It can be expressed as 2 * n + 1, where 'n' is again any integer. Examples are 1, 3, 5, 7, 9, 11, and, of course, 15.
Therefore, since 15 cannot be divided evenly by 2 (15 ÷ 2 = 7 with a remainder of 1), it falls squarely into the category of odd numbers.
Determining Odd and Even Numbers: Practical Methods
While the definitions are clear, let's explore practical methods for determining whether a number is odd or even. This is particularly useful when dealing with larger numbers.
-
Division by 2: The most straightforward method is simply dividing the number by 2. If the result is a whole number (no remainder), the number is even. If there's a remainder of 1, the number is odd.
-
Last Digit Check: A quicker, albeit less fundamental, method involves examining the last digit of the number. If the last digit is 0, 2, 4, 6, or 8, the number is even. If the last digit is 1, 3, 5, 7, or 9, the number is odd. This works because the last digit determines the remainder when dividing by 10, which in turn affects divisibility by 2.
Let's apply these methods to 15:
- Division by 2: 15 ÷ 2 = 7 with a remainder of 1. Therefore, 15 is odd.
- Last Digit Check: The last digit of 15 is 5, which is part of the odd digit set. Therefore, 15 is odd.
Both methods confirm that 15 is indeed an odd number.
Properties of Odd and Even Numbers: Beyond the Basics
Odd and even numbers exhibit several interesting properties when subjected to various mathematical operations. Understanding these properties can be crucial in various mathematical proofs and problem-solving scenarios.
-
Addition and Subtraction:
- Even + Even = Even
- Odd + Odd = Even
- Even + Odd = Odd
- Even - Even = Even
- Odd - Odd = Even
- Even - Odd = Odd
- Odd - Even = Odd
-
Multiplication:
- Even × Even = Even
- Odd × Odd = Odd
- Even × Odd = Even
-
Squares and Cubes:
- The square of an even number is always even.
- The square of an odd number is always odd.
- The cube of an even number is always even.
- The cube of an odd number is always odd.
These properties are readily demonstrable and can be proven using algebraic manipulations based on the 2n and 2n+1 definitions. For instance, (2n)² = 4n² = 2(2n²), showing that the square of an even number is always even because it's divisible by 2. Similarly, (2n+1)² = 4n² + 4n + 1 = 2(2n² + 2n) + 1, showing that the square of an odd number will always leave a remainder of 1 when divided by 2, hence it's odd.
These properties extend to higher powers as well. Understanding these patterns is fundamental in number theory and algebra.
Odd and Even Numbers in Number Theory and Beyond
The seemingly simple distinction between odd and even numbers underpins many sophisticated concepts within number theory. These concepts have practical applications in various fields, including:
-
Cryptography: The security of many cryptographic systems relies on the properties of prime numbers, which are closely related to odd and even numbers. Many prime numbers (except 2) are odd.
-
Computer Science: Bitwise operations, fundamental in computer programming, rely heavily on the binary representation of numbers, which directly relates to even and odd numbers (a number ending in 0 is even in binary, a number ending in 1 is odd).
-
Combinatorics and Probability: Calculating probabilities and combinations often involves considering the parity (oddness or evenness) of numbers.
Historical Context: A Glimpse into the Past
The concepts of odd and even numbers are ancient, tracing back to the earliest civilizations. Evidence suggests that the Babylonians and Egyptians understood these concepts thousands of years ago. The Greeks, particularly Pythagoras and his followers, deeply explored number theory, including the properties of odd and even numbers, assigning philosophical and mystical significance to them.
Frequently Asked Questions (FAQ)
Q: Are there any exceptions to the rules regarding odd and even numbers?
A: No. The rules concerning addition, subtraction, and multiplication of odd and even numbers are consistent and universally applicable to all integers.
Q: Can a number be both odd and even?
A: No. A number can only be either odd or even; it cannot be both. This is a direct consequence of the definition – a number is either divisible by 2 or it isn't.
Q: What about zero? Is it odd or even?
A: Zero is considered an even number because it is perfectly divisible by 2 (0 ÷ 2 = 0).
Q: How are odd and even numbers used in real-world applications?
A: Beyond the theoretical applications mentioned earlier, odd and even numbers find practical uses in scheduling, resource allocation, and even in simple tasks like determining if a number of items can be divided equally among a group of people.
Conclusion: The Significance of Simple Concepts
While the question, "Is 15 an odd number?" might seem trivial, it serves as a gateway to understanding a fundamental concept in mathematics. The distinction between odd and even numbers, seemingly simple, forms the bedrock of many advanced mathematical ideas and has profound implications in diverse fields. By understanding the definitions, properties, and applications of odd and even numbers, we gain a deeper appreciation for the intricate beauty and power of mathematics. Remember, even the most basic concepts can lead to unexpected and fascinating discoveries. The fact that 15 is definitively an odd number is not just a simple answer but a stepping stone to a much broader and more enriching mathematical journey.
Latest Posts
Latest Posts
-
200cm Is How Many Feet
Sep 12, 2025
-
Angle Between 2 Vectors Calculator
Sep 12, 2025
-
3000 Sq Ft To M2
Sep 12, 2025
-
Abiotic Elements In The Rainforest
Sep 12, 2025
-
Is 43 Prime Or Composite
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Is 15 An Odd Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.