Is -15 A Rational Number
seoindie
Sep 23, 2025 · 6 min read
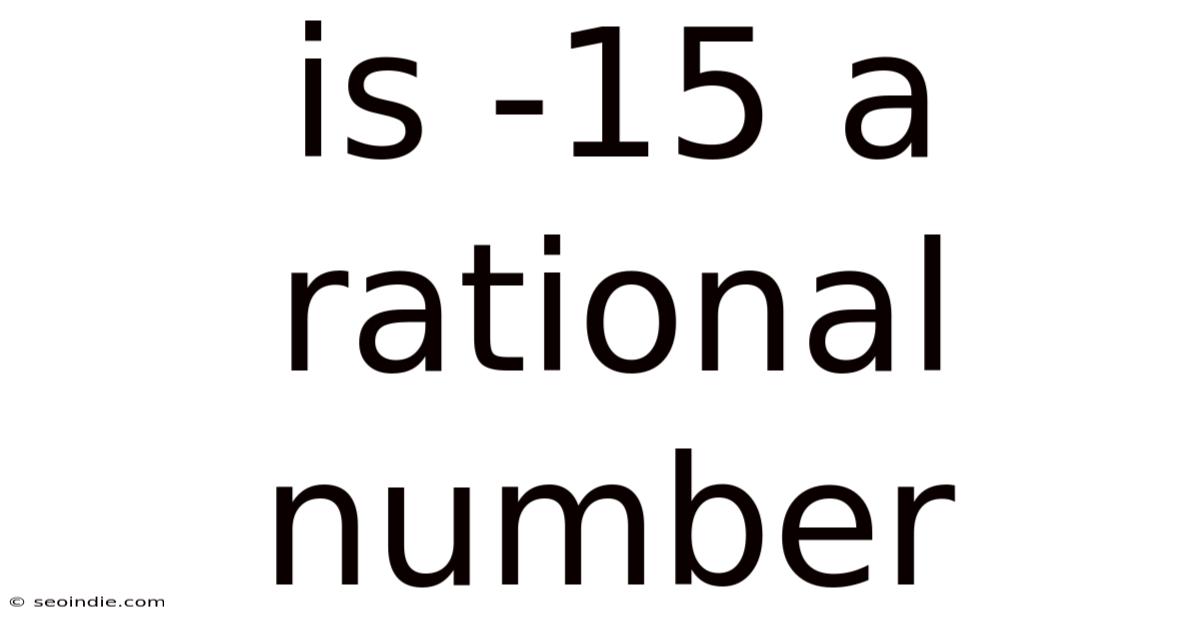
Table of Contents
Is -15 a Rational Number? A Deep Dive into Rational Numbers and Their Properties
Is -15 a rational number? The answer is a resounding yes, but understanding why requires a deeper exploration into the definition and properties of rational numbers. This article will not only definitively answer this question but also provide a comprehensive understanding of rational numbers, their characteristics, and how to identify them. We'll delve into the mathematical concepts involved, offering clear explanations and examples to solidify your understanding. By the end, you'll not only know that -15 is a rational number but also possess a robust grasp of the broader topic.
Understanding Rational Numbers: The Foundation
A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p is the numerator and q is the non-zero denominator. This seemingly simple definition holds the key to understanding a vast class of numbers. The crucial elements are:
- Integers: Integers are whole numbers, including zero, and their negative counterparts. Examples include -3, 0, 5, 100, and -1000.
- Fraction: A fraction represents a part of a whole. It's the ratio of two numbers, the numerator divided by the denominator.
- Non-zero denominator: The denominator, q, cannot be zero. Division by zero is undefined in mathematics.
Let's look at some examples of rational numbers:
- 1/2: This is a classic example. Both 1 and 2 are integers, and 2 is not zero.
- -3/4: Again, both -3 and 4 are integers, and 4 is not zero.
- 5: The number 5 can be expressed as 5/1, fulfilling the definition. Every integer is a rational number.
- 0: Zero can be expressed as 0/1, making it a rational number.
- 0.75: This decimal can be written as the fraction 3/4, satisfying the definition.
Why -15 is a Rational Number
Now, let's directly address the question: Is -15 a rational number? The answer is yes, and here's why:
-15 can be expressed as the fraction -15/1.
Both -15 and 1 are integers, and the denominator, 1, is not zero. This perfectly satisfies the definition of a rational number. Therefore, -15 is unequivocally a rational number.
Exploring Different Representations of Rational Numbers
Rational numbers can be expressed in several forms:
- Fractions: This is the most fundamental representation, as defined earlier.
- Decimals: Rational numbers, when expressed as decimals, either terminate (end) or repeat in a predictable pattern. For instance, 1/4 = 0.25 (terminating), while 1/3 = 0.333... (repeating).
- Percentages: Percentages are simply fractions expressed as a proportion of 100. For example, 1/4 is equivalent to 25%.
The ability to represent a number in these various forms doesn't change its classification as a rational number. The underlying condition remains: it must be expressible as a fraction of two integers with a non-zero denominator.
Distinguishing Rational Numbers from Irrational Numbers
It's important to contrast rational numbers with irrational numbers. Irrational numbers cannot be expressed as a fraction of two integers. Their decimal representations neither terminate nor repeat. Famous examples include:
- π (pi): Approximately 3.14159..., its digits continue infinitely without a repeating pattern.
- √2 (the square root of 2): Approximately 1.414..., also with an infinite, non-repeating decimal expansion.
- e (Euler's number): Approximately 2.71828..., another example of an irrational number.
Understanding the difference between rational and irrational numbers is crucial in mathematics. Their properties and behaviors are significantly different.
Properties of Rational Numbers
Rational numbers possess several important properties:
- Closure under addition, subtraction, multiplication, and division (excluding division by zero): When you add, subtract, multiply, or divide two rational numbers (excluding division by zero), the result is always another rational number.
- Density: Between any two rational numbers, there exists infinitely many other rational numbers.
- Ordered: Rational numbers can be ordered; you can always determine which of two rational numbers is greater or smaller.
- Commutative property of addition and multiplication: The order of operation doesn't matter for addition and multiplication. For example, a + b = b + a, and a * b = b * a.
- Associative property of addition and multiplication: The grouping of numbers doesn't matter for addition and multiplication. For example, (a + b) + c = a + (b + c), and (a * b) * c = a * (b * c).
- Distributive property: Multiplication distributes over addition. For example, a * (b + c) = a * b + a * c.
Practical Applications of Rational Numbers
Rational numbers are fundamental to many areas of mathematics and everyday life:
- Measurements: Lengths, weights, volumes, and other measurements are often expressed using rational numbers.
- Finance: Money transactions and calculations involve rational numbers extensively.
- Engineering: Design and construction rely heavily on precise calculations with rational numbers.
- Computer Science: Representing numbers in computers often involves rational approximations.
- Physics: Many physical laws and calculations involve rational numbers.
Working with Rational Numbers: Examples and Exercises
Let's reinforce our understanding with some examples:
Example 1: Simplify the fraction 12/18.
To simplify, we find the greatest common divisor (GCD) of 12 and 18, which is 6. Dividing both the numerator and denominator by 6, we get 2/3.
Example 2: Convert the decimal 0.6 to a fraction.
0.6 can be written as 6/10. Simplifying by dividing both by 2, we get 3/5.
Example 3: Add the fractions 1/3 and 2/5.
To add fractions, we need a common denominator. The least common multiple (LCM) of 3 and 5 is 15. We rewrite the fractions: (1/3) * (5/5) = 5/15 and (2/5) * (3/3) = 6/15. Adding them, we get 11/15.
Exercise 1: Is -2/3 a rational number? Explain your answer.
Exercise 2: Convert the decimal 0.125 to a fraction.
Exercise 3: Subtract 2/7 from 3/4.
Frequently Asked Questions (FAQ)
Q1: Can a rational number be negative?
A1: Yes, absolutely. As we've seen with -15 and -3/4, rational numbers can be negative. The sign simply indicates the direction on the number line.
Q2: Are all integers rational numbers?
A2: Yes, every integer can be expressed as a fraction with a denominator of 1, thus satisfying the definition of a rational number.
Q3: Are all fractions rational numbers?
A3: Yes, as long as both the numerator and denominator are integers, and the denominator is not zero.
Q4: How can I determine if a decimal is a rational number?
A4: If the decimal terminates (ends) or repeats in a predictable pattern, it's a rational number. If it goes on forever without a repeating pattern, it's irrational.
Q5: What is the difference between a rational and an irrational number?
A5: A rational number can be expressed as a fraction of two integers (with a non-zero denominator). An irrational number cannot be expressed as such; its decimal representation is infinite and non-repeating.
Conclusion: A Solid Understanding of Rational Numbers
We've comprehensively explored the concept of rational numbers, solidifying the understanding that -15 is indeed a rational number because it fits the definition perfectly: it can be expressed as the fraction -15/1. Beyond this specific example, we’ve delved into the fundamental properties of rational numbers, distinguishing them from irrational numbers, and exploring their diverse representations and applications. This thorough examination equips you not only to answer the initial question confidently but also to approach more complex mathematical concepts with greater assurance and understanding. Remember, a strong foundation in fundamental mathematical concepts is key to unlocking advanced knowledge.
Latest Posts
Latest Posts
-
Projects Of The Solar System
Sep 24, 2025
-
What Roman Numeral Is 35
Sep 24, 2025
-
When To Use An Exclamation
Sep 24, 2025
-
Multiples Of 6 To 100
Sep 24, 2025
-
Is 77 Prime Or Composite
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Is -15 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.