Is 1/4 Bigger Than 3/4
seoindie
Sep 18, 2025 · 6 min read
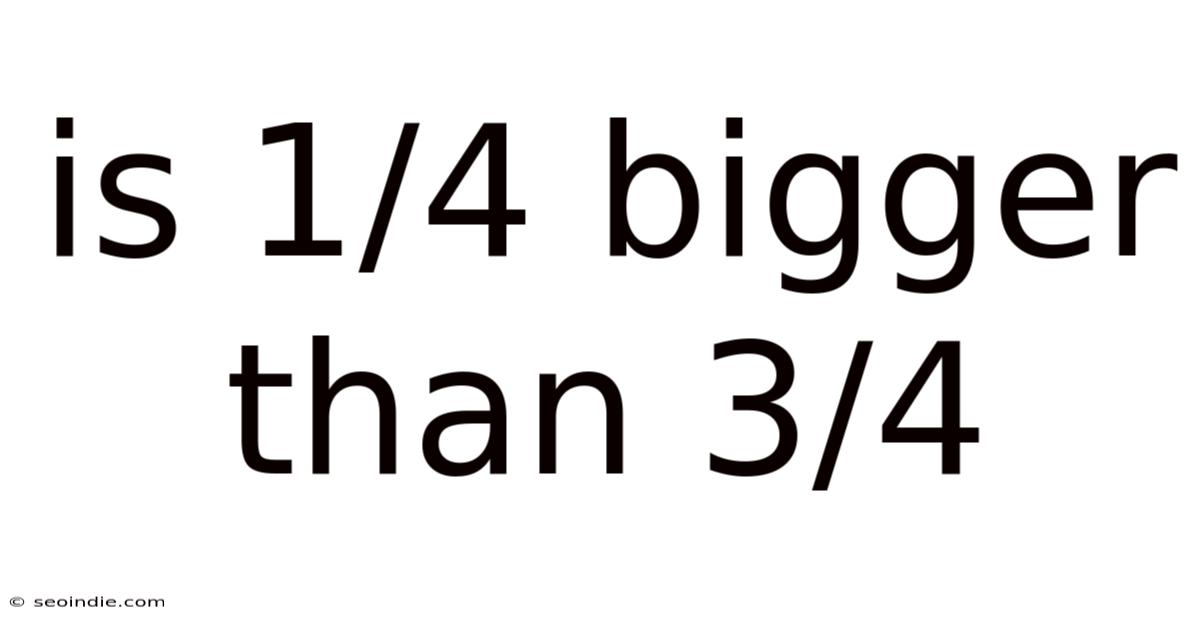
Table of Contents
Is 1/4 Bigger Than 3/4? Understanding Fractions and Comparisons
Is 1/4 bigger than 3/4? The answer might seem obvious to some, but understanding why one fraction is larger than another is crucial for mastering fundamental math concepts. This article dives deep into comparing fractions, exploring various methods, and building a solid understanding of fraction manipulation. We'll cover not only the simple answer but also delve into the underlying principles, providing you with the tools to confidently compare any two fractions.
Introduction: Understanding Fractions
Before we tackle the core question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator tells us how many of those parts we're considering.
For example, in the fraction 3/4, the denominator (4) indicates that the whole is divided into four equal parts. The numerator (3) indicates that we're considering three of those four parts. Similarly, 1/4 means one out of four equal parts.
Visualizing the Comparison: The Power of Representation
One of the simplest ways to compare fractions is through visualization. Imagine a pizza cut into four equal slices.
- 1/4: This represents one slice of the pizza.
- 3/4: This represents three slices of the pizza.
Looking at this visual representation, it's instantly clear that 3/4 (three slices) is significantly larger than 1/4 (one slice). This visual approach is incredibly effective for grasping the concept, particularly for beginners.
Comparing Fractions: Different Approaches
While visualization is helpful for simple fractions, it becomes less practical with more complex ones. Let's explore more robust methods for comparing fractions:
1. Common Denominator Method: This is the most widely used and reliable method. To compare fractions using this method, we need to find a common denominator – a number that is a multiple of both denominators.
Let's compare 1/4 and 3/4. Both fractions already share a common denominator: 4. Since the denominators are the same, we can directly compare the numerators. Because 1 < 3, we conclude that 1/4 < 3/4.
Example with Different Denominators: Let's compare 2/3 and 3/5. The least common denominator (LCD) is 15 (3 x 5 = 15). We convert both fractions to have a denominator of 15:
- 2/3 = (2 x 5) / (3 x 5) = 10/15
- 3/5 = (3 x 3) / (5 x 3) = 9/15
Now, we can easily compare the numerators: 10 > 9, therefore 2/3 > 3/5.
2. Cross-Multiplication Method: This method is particularly useful when finding a common denominator is cumbersome. To compare fractions a/b and c/d, we cross-multiply:
- a x d and b x c
If a x d > b x c, then a/b > c/d. If a x d < b x c, then a/b < c/d.
Let's use this method to compare 1/4 and 3/4:
- 1 x 4 = 4
- 4 x 3 = 12
Since 4 < 12, we confirm that 1/4 < 3/4.
Example with different denominators: Let's compare 5/7 and 2/3:
- 5 x 3 = 15
- 7 x 2 = 14
Since 15 > 14, 5/7 > 2/3
3. Converting to Decimals: Another way to compare fractions is by converting them to decimals. This method is particularly helpful when dealing with fractions that are difficult to compare using other methods. To convert a fraction to a decimal, simply divide the numerator by the denominator.
- 1/4 = 0.25
- 3/4 = 0.75
Clearly, 0.75 > 0.25, so 3/4 > 1/4
Understanding the Relationship Between Numerator and Denominator
The size of a fraction is directly influenced by the relationship between its numerator and denominator.
- Numerator significantly smaller than the denominator: This indicates a small fraction, close to zero (e.g., 1/100).
- Numerator close to the denominator: This indicates a fraction close to one (e.g., 99/100).
- Numerator larger than the denominator: This represents an improper fraction, which is greater than one (e.g., 5/4).
Applying the Concepts to More Complex Scenarios
The techniques described above apply equally well to more complex fractions, even those with larger numbers or different denominators. The key is to choose the method that best suits the specific fractions you're comparing. Remember, practice is key to mastering fraction comparison!
Frequently Asked Questions (FAQ)
Q: Can I always use the common denominator method?
A: Yes, the common denominator method is always reliable. However, finding the least common denominator (LCD) can sometimes be time-consuming, especially with larger numbers. In such cases, cross-multiplication might be more efficient.
Q: What if I have a mixed number (a whole number and a fraction)?
A: Convert mixed numbers to improper fractions before comparing them using any of the methods mentioned above. For example, 1 1/2 becomes 3/2.
Q: Are there any online tools or calculators that can help me compare fractions?
A: While there are many online fraction calculators available, understanding the underlying principles is far more valuable than relying solely on a tool. Calculators are useful for checking your work, but they shouldn't replace your understanding of the methods.
Q: Why is understanding fraction comparison important?
A: Fraction comparison is a foundational skill in mathematics. It underpins a vast range of concepts, from basic arithmetic to advanced algebra and calculus. Mastering this skill will significantly improve your mathematical abilities and problem-solving skills.
Conclusion: Mastering Fractions for a Brighter Future
The simple answer to "Is 1/4 bigger than 3/4?" is a resounding no. 3/4 is significantly larger than 1/4. However, this article has gone beyond simply providing the answer; it has equipped you with the knowledge and techniques to confidently compare any two fractions. By understanding the different methods – visualization, common denominators, cross-multiplication, and decimal conversion – you can approach fraction comparison with confidence and efficiency. Remember, mastering fractions isn't just about memorizing rules; it's about developing a deep understanding of their underlying principles. This understanding will serve you well throughout your mathematical journey and beyond. Consistent practice and application of these techniques will build your confidence and solidify your grasp of this critical mathematical concept. The power of understanding fractions extends far beyond the classroom; it's a skill applicable to numerous real-world scenarios, from cooking and construction to finance and engineering. So embrace the challenge, practice regularly, and watch your mathematical prowess blossom!
Latest Posts
Latest Posts
-
We Could Definitely Do That
Sep 18, 2025
-
What Is On A Globe
Sep 18, 2025
-
Center Of Mass For Triangle
Sep 18, 2025
-
Words That Start With Mus
Sep 18, 2025
-
Difference Between Empire And Kingdom
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Is 1/4 Bigger Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.