Is 1/2 More Than 2/3
seoindie
Sep 17, 2025 · 5 min read
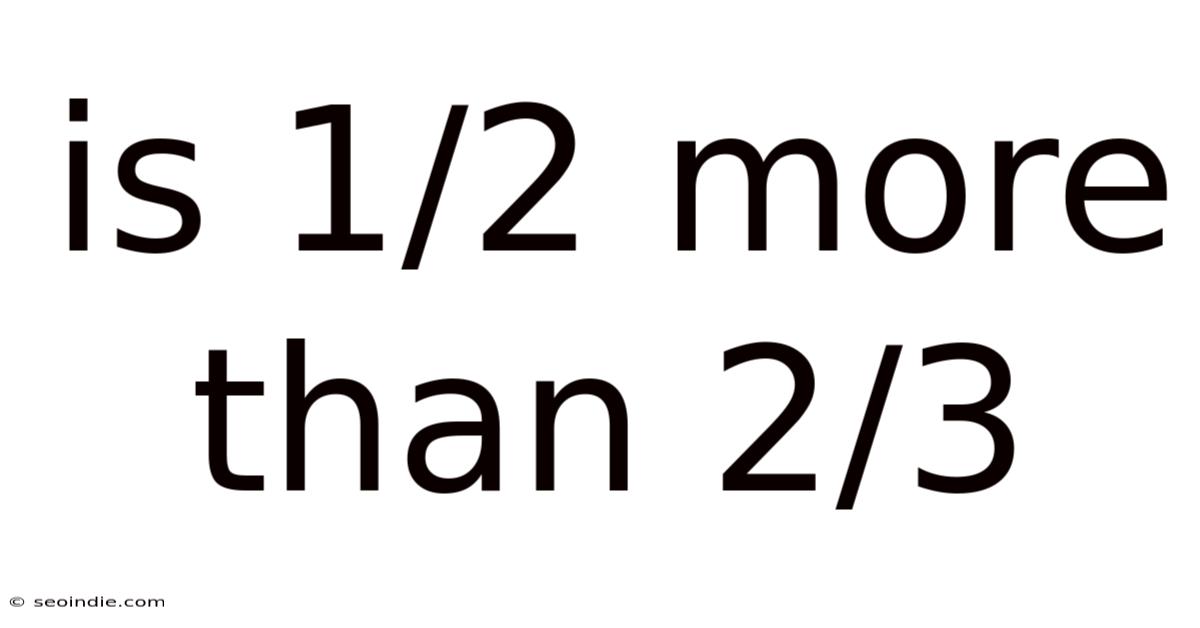
Table of Contents
Is 1/2 More Than 2/3? Understanding Fractions and Comparisons
Is 1/2 more than 2/3? This seemingly simple question touches upon a fundamental concept in mathematics: comparing fractions. Understanding how to compare fractions is crucial for various applications, from baking and cooking to advanced engineering and financial calculations. This article will delve into the methods of comparing fractions, definitively answer the question, and explore the broader mathematical concepts involved. We will also tackle common misconceptions and frequently asked questions to ensure a comprehensive understanding.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 1/2, the whole is divided into two equal parts, and we are considering one of those parts.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This involves converting both fractions so they have the same denominator. Once they share a denominator, we can simply compare the numerators. The fraction with the larger numerator is the larger fraction.
Let's apply this method to compare 1/2 and 2/3:
-
Find the least common multiple (LCM) of the denominators: The denominators are 2 and 3. The LCM of 2 and 3 is 6.
-
Convert the fractions to equivalent fractions with the common denominator:
-
To convert 1/2 to a fraction with a denominator of 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6
-
To convert 2/3 to a fraction with a denominator of 6, we multiply both the numerator and the denominator by 2: (2 x 2) / (3 x 2) = 4/6
-
-
Compare the numerators: Now we have 3/6 and 4/6. Since 3 < 4, we can conclude that 3/6 < 4/6.
-
Conclusion: Therefore, 1/2 is less than 2/3.
Method 2: Converting to Decimals
Another way to compare fractions is to convert them into decimals. This involves dividing the numerator by the denominator for each fraction.
Let's apply this method:
-
Convert 1/2 to a decimal: 1 ÷ 2 = 0.5
-
Convert 2/3 to a decimal: 2 ÷ 3 = 0.666... (a repeating decimal)
-
Compare the decimals: 0.5 < 0.666...
-
Conclusion: Therefore, 1/2 is less than 2/3.
Method 3: Visual Representation
Visualizing fractions can be a helpful approach, especially for beginners. Imagine two identical pizzas.
- For 1/2, you cut the pizza into two equal slices and take one.
- For 2/3, you cut the pizza into three equal slices and take two.
By visually comparing the amount of pizza you have in each case, it's clear that two-thirds of a pizza is larger than one-half.
Addressing Common Misconceptions
A common mistake is to assume that because the numerator of 2/3 is larger than the numerator of 1/2, 2/3 must be larger. This is incorrect because the denominators are different. The denominator indicates the size of the fractional parts, and ignoring it leads to inaccurate comparisons.
Another misconception stems from focusing solely on the magnitude of the numbers without considering their context within the fraction. Simply looking at "2" being larger than "1" without considering the denominators will lead to an erroneous conclusion.
The Importance of Understanding Fraction Comparisons
The ability to compare fractions is essential for various aspects of life:
- Cooking and Baking: Following recipes often involves understanding fraction measurements (e.g., 1/2 cup vs. 2/3 cup).
- Construction and Engineering: Precise measurements and calculations rely heavily on understanding and comparing fractions.
- Finance: Calculating proportions, percentages, and interest rates involves working with fractions.
- Data Analysis: Interpreting data represented in fractions or proportions necessitates comparing fractional values.
Frequently Asked Questions (FAQ)
Q: Can I always use the common denominator method?
A: Yes, the common denominator method is a universally applicable and reliable technique for comparing any two fractions.
Q: What if the fractions have very large denominators?
A: While finding the LCM for large denominators can be more time-consuming, the principle remains the same. You can still find the LCM and convert the fractions to have a common denominator. Alternatively, converting to decimals can be a more efficient approach in such cases.
Q: Are there other methods for comparing fractions besides these three?
A: While these are the most common and straightforward methods, there are other approaches, particularly for specific types of fractions, such as comparing fractions with the same numerator or denominator.
Q: What if I have more than two fractions to compare?
A: You can extend the common denominator method to compare multiple fractions. Find the LCM of all the denominators, convert all fractions to have this common denominator, and then compare the numerators.
Q: Why is it important to learn different methods for comparing fractions?
A: Learning different methods provides flexibility and efficiency. Depending on the specific fractions and the context, one method might be quicker or easier than another. Having multiple approaches solidifies your understanding and makes you a more versatile problem-solver.
Conclusion
In conclusion, 1/2 is not more than 2/3; it is less than 2/3. Understanding how to compare fractions is a cornerstone of mathematical literacy. This article has provided multiple methods for comparison—finding a common denominator, converting to decimals, and visual representation—to cater to different learning styles and preferences. Mastering these techniques equips you with a crucial skill applicable to various aspects of life, from everyday tasks to more complex calculations. Remember to always focus on the relationship between the numerator and denominator when comparing fractions, avoiding common pitfalls and misconceptions. Consistent practice and a clear understanding of the underlying concepts are key to mastering fraction comparison.
Latest Posts
Latest Posts
-
Pcr Forward And Reverse Primer
Sep 17, 2025
-
Cursive From A To Z
Sep 17, 2025
-
What Numbers Go Into 56
Sep 17, 2025
-
Equation For Paired T Test
Sep 17, 2025
-
Lcm Of 6 And 24
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 More Than 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.