Is 1/2 Greater Than 1/3
seoindie
Sep 23, 2025 · 6 min read
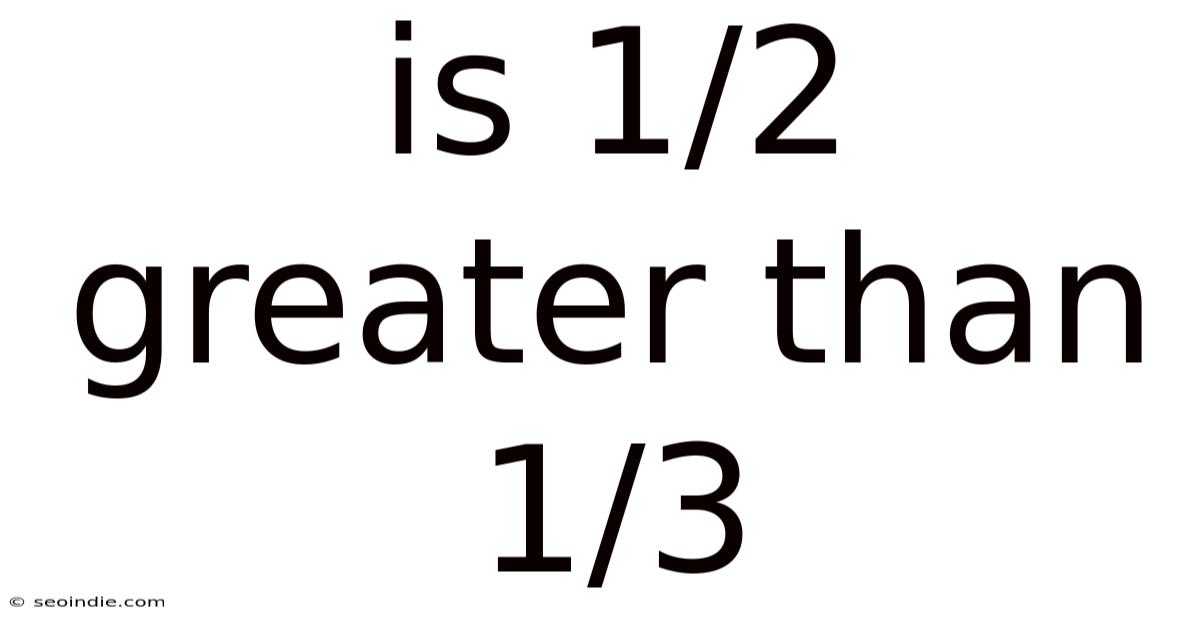
Table of Contents
Is 1/2 Greater Than 1/3? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental concept in mathematics, crucial for everyday life and advanced studies. This article will thoroughly explore the question: is 1/2 greater than 1/3? We'll not only answer this question definitively but also delve into the underlying principles of comparing fractions, offering multiple methods to tackle similar problems. This exploration will equip you with the tools to confidently compare any two fractions.
Introduction: Understanding Fractions
Before jumping into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: a numerator (the top number) and a denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, and the numerator tells us how many of those parts we have. For example, in the fraction 1/2, the whole is divided into two equal parts, and we have one of those parts.
Is 1/2 Greater Than 1/3? The Simple Answer
Yes, 1/2 is greater than 1/3. This might seem obvious intuitively, but understanding why it's true is essential for grasping fraction comparison.
Method 1: Visual Representation
One of the easiest ways to compare fractions is through visual representation. Imagine two identical pizzas.
- Pizza 1: Cut into two equal slices. You eat one slice (1/2).
- Pizza 2: Cut into three equal slices. You eat one slice (1/3).
Which pizza leaves you with more uneaten pizza? Clearly, Pizza 2 leaves you with a larger portion. This visual demonstrates that 1/2 is larger than 1/3 because you're taking a larger portion of the whole in the first scenario.
Method 2: Finding a Common Denominator
A more robust method for comparing fractions involves finding a common denominator. A common denominator is a number that is a multiple of both denominators. For 1/2 and 1/3, the least common multiple (LCM) of 2 and 3 is 6.
- Convert 1/2: To get a denominator of 6, we multiply both the numerator and denominator of 1/2 by 3: (1 x 3) / (2 x 3) = 3/6
- Convert 1/3: To get a denominator of 6, we multiply both the numerator and denominator of 1/3 by 2: (1 x 2) / (3 x 2) = 2/6
Now we can easily compare 3/6 and 2/6. Since 3 > 2, we conclude that 3/6 > 2/6, and therefore, 1/2 > 1/3.
This method works for any two fractions, making it a powerful tool in fraction comparison. Finding the LCM might require some prime factorization knowledge for larger numbers, but the process remains consistent.
Method 3: Decimal Conversion
Another way to compare fractions is by converting them into decimals. This method is particularly helpful when dealing with fractions that are difficult to visualize or find a common denominator for quickly.
- Convert 1/2 to a decimal: 1 ÷ 2 = 0.5
- Convert 1/3 to a decimal: 1 ÷ 3 = 0.333... (a repeating decimal)
Comparing 0.5 and 0.333..., it's clear that 0.5 (or 1/2) is greater. This method provides a straightforward comparison, especially when using a calculator. However, remember that repeating decimals might require careful attention to ensure accurate comparison.
Method 4: Using a Number Line
A number line offers a visual comparison tool. Place both fractions on the number line. The fraction further to the right is the larger fraction. Since 1/2 is closer to 1 than 1/3, it visually represents its greater value. This method works well for intuitive understanding but might not be as precise as the other methods for complex fractions.
Extending the Concept: Comparing More Complex Fractions
The methods described above apply to more complex fractions as well. Let's consider comparing 5/8 and 2/3.
Using the common denominator method:
- The LCM of 8 and 3 is 24.
- 5/8 becomes (5 x 3) / (8 x 3) = 15/24
- 2/3 becomes (2 x 8) / (3 x 8) = 16/24
- Since 16 > 15, we conclude that 2/3 > 5/8.
Using decimal conversion:
- 5/8 = 0.625
- 2/3 = 0.666...
- Again, 2/3 is greater.
Understanding the Relationship Between Numerator and Denominator
The size of a fraction is directly related to the relationship between its numerator and denominator.
- Numerator significantly smaller than denominator: The fraction will be close to zero. For instance, 1/100 is a small fraction.
- Numerator close to the denominator: The fraction is close to one. For example, 99/100 is close to one.
- Numerator equal to the denominator: The fraction equals one. For example, 5/5 = 1.
- Numerator larger than the denominator: The fraction is greater than one (an improper fraction). For example, 7/3 is greater than one.
Frequently Asked Questions (FAQs)
Q1: Why is finding a common denominator important for comparing fractions?
A1: Finding a common denominator allows us to express the fractions with the same "unit of measurement." Only then can we directly compare the numerators to determine which fraction represents a larger portion of the whole.
Q2: What if the fractions have very large denominators? Is there a faster method?
A2: While finding the LCM for very large numbers can be time-consuming, using decimal conversion with a calculator becomes much more efficient.
Q3: Can I compare fractions by just looking at the numerators or denominators?
A3: No, comparing only numerators or denominators is insufficient. You need to consider the relationship between the numerator and the denominator. For example, while 2 > 1, that doesn't mean 2/10 > 1/2 (or 0.2 > 0.5).
Q4: Are there other methods to compare fractions besides those mentioned?
A4: Yes, there are. More advanced methods exist, such as using cross-multiplication, which is essentially a shortcut to the common denominator method. However, the methods explained here provide a solid foundation for understanding the underlying principles of fraction comparison.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a core skill in mathematics. This article has explored various methods to effectively compare fractions, from intuitive visual representations to more rigorous mathematical techniques like finding common denominators and converting to decimals. Mastering these methods empowers you to confidently tackle fraction comparison problems of varying complexity, strengthening your foundational understanding of numbers and mathematical reasoning. Remember, the key is to understand the relationship between the numerator and the denominator, and to choose the most efficient method depending on the complexity of the fractions involved. Through consistent practice and application, you'll build a strong and confident grasp of this essential mathematical skill.
Latest Posts
Latest Posts
-
First 20 Elements Electronic Configuration
Sep 23, 2025
-
Gcf Of 45 And 25
Sep 23, 2025
-
Adjectives To Describe A Tree
Sep 23, 2025
-
Meaning Of Non Biodegradable Waste
Sep 23, 2025
-
Verb That Starts With V
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Greater Than 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.