Is 1/2 Greater Than 1
seoindie
Sep 16, 2025 · 5 min read
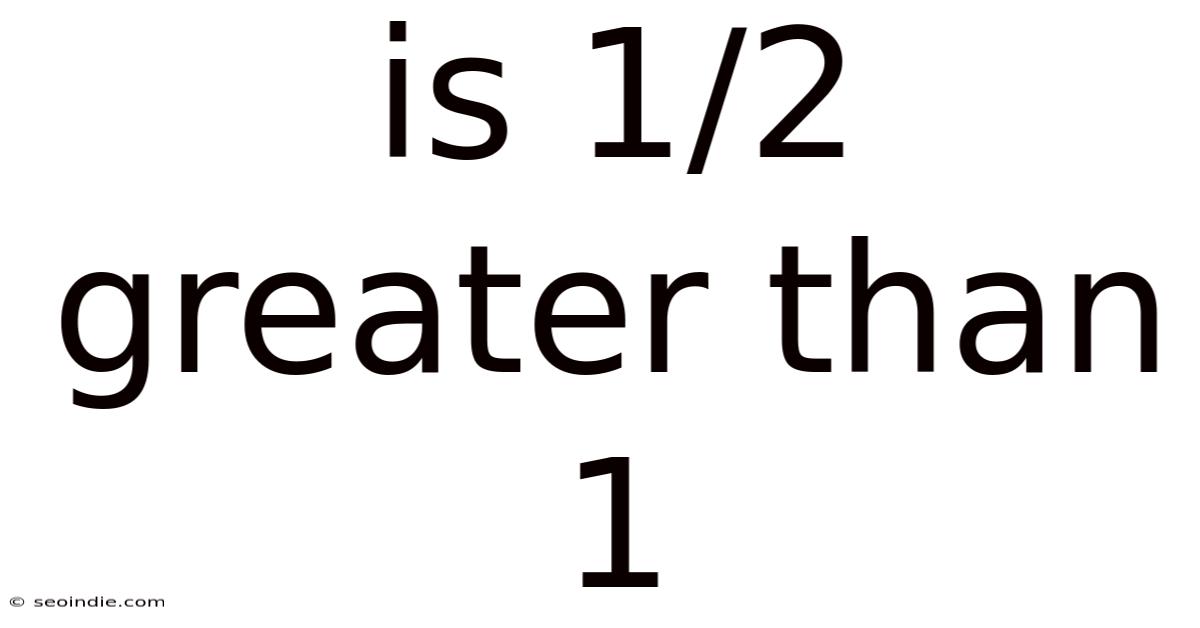
Table of Contents
Is 1/2 Greater Than 1? Understanding Fractions and Comparisons
The question, "Is 1/2 greater than 1?" might seem deceptively simple, especially for those comfortable with basic arithmetic. However, understanding the underlying principles of fractions and how to compare them is crucial for developing a solid foundation in mathematics. This article will delve into the answer, exploring the concept of fractions, providing methods for comparing them, and addressing common misconceptions. We'll also explore why this seemingly straightforward question is important for understanding more advanced mathematical concepts.
Introduction to Fractions
A fraction represents a part of a whole. It's written as a ratio of two numbers: a numerator (the top number) and a denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 1/2, the denominator 2 means the whole is divided into two equal parts, and the numerator 1 means we're considering one of those parts.
Understanding fractions is fundamental to many areas of life, from cooking (following a recipe that calls for 1/4 cup of sugar) to construction (measuring precise lengths using fractions of an inch) and finance (understanding percentages and proportions). Mastering fractions provides a strong base for tackling more complex mathematical problems involving ratios, proportions, decimals, and percentages.
Comparing Fractions: A Step-by-Step Guide
To determine whether 1/2 is greater than 1, we need to understand how to compare fractions. There are several methods, each useful in different situations.
Method 1: Visual Representation
One of the easiest ways to compare fractions is to visualize them. Imagine a pizza cut into two equal slices. 1/2 represents one of those slices. The whole pizza represents the number 1. Clearly, one slice (1/2) is smaller than the entire pizza (1). This visual approach makes the comparison intuitive.
Method 2: Using a Common Denominator
This method is particularly useful when comparing fractions with different denominators. To compare fractions, we need to express them with a common denominator. Let's compare 1/2 and 1. We can rewrite 1 as a fraction with a denominator of 2: 1 = 2/2. Now, we can easily compare 1/2 and 2/2. Since 1/2 < 2/2, we can conclude that 1/2 is not greater than 1.
Method 3: Converting to Decimals
Another effective approach involves converting fractions into decimals. To convert a fraction to a decimal, divide the numerator by the denominator. For 1/2, this is 1 ÷ 2 = 0.5. Since 0.5 is less than 1, we confirm that 1/2 is not greater than 1. This method is especially helpful when dealing with more complex fractions.
Method 4: Understanding the Relationship Between Numerator and Denominator
In a proper fraction (where the numerator is smaller than the denominator), the fraction will always be less than 1. An improper fraction (where the numerator is equal to or greater than the denominator) is equal to or greater than 1. Since 1/2 is a proper fraction, it must be less than 1.
Why This Comparison Matters: Building a Strong Mathematical Foundation
Understanding the relationship between fractions and whole numbers is fundamental to grasping more advanced mathematical concepts. This seemingly simple comparison exercise lays the groundwork for:
- Algebra: Solving algebraic equations often involves manipulating fractions and understanding their relationships.
- Calculus: Derivatives and integrals frequently involve working with fractions and limits, requiring a strong understanding of fractional comparisons.
- Geometry: Calculating areas and volumes often necessitates working with fractions and proportions.
- Probability and Statistics: Understanding probabilities and proportions is essential in many statistical analyses, requiring a firm grasp of fractional representation.
Addressing Common Misconceptions
Several common misconceptions can lead to errors when comparing fractions.
- Assuming larger numerators mean larger fractions: This is only true if the denominators are the same. For example, 3/4 > 1/4, but 1/2 > 1/4 even though 1 < 3.
- Ignoring the denominator: The denominator is crucial; it determines the size of the parts into which the whole is divided.
- Difficulty visualizing fractions: Many struggle to visualize fractions accurately. Using visual aids like pie charts or fraction bars can greatly improve understanding.
Frequently Asked Questions (FAQ)
Q: How can I compare fractions with different numerators and denominators?
A: The most reliable method is to find a common denominator. Convert each fraction to an equivalent fraction with the common denominator, then compare the numerators. Alternatively, convert them to decimals for easier comparison.
Q: What is an improper fraction?
A: An improper fraction is a fraction where the numerator is greater than or equal to the denominator. It represents a value greater than or equal to 1.
Q: What is a mixed number?
A: A mixed number combines a whole number and a proper fraction (e.g., 1 1/2). It represents a value greater than 1.
Q: How can I simplify fractions?
A: To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator, and divide both by the GCD. For example, 4/6 can be simplified to 2/3 by dividing both numerator and denominator by 2 (their GCD).
Q: What are equivalent fractions?
A: Equivalent fractions represent the same value even though they have different numerators and denominators. For example, 1/2, 2/4, and 3/6 are all equivalent fractions.
Conclusion: Mastering Fractions, Mastering Mathematics
The question, "Is 1/2 greater than 1?" provides a seemingly simple entry point to explore the critical concept of fractions. Understanding how to compare fractions is not merely about solving a single problem; it's about building a strong foundation in mathematics. By mastering the concepts presented here—visualizing fractions, finding common denominators, converting to decimals, and understanding the relationship between numerators and denominators—you'll be well-equipped to tackle more complex mathematical challenges and appreciate the interconnectedness of mathematical concepts. Remember to practice regularly and utilize various methods to solidify your understanding of fractions. The more you practice, the more confident and proficient you will become in handling fractions and other mathematical concepts. This foundational understanding will serve you well throughout your mathematical journey.
Latest Posts
Latest Posts
-
What Is The Hottest Layer
Sep 16, 2025
-
Whats The Factors Of 15
Sep 16, 2025
-
Cbse Class 7th Science Book
Sep 16, 2025
-
Words That End In Sae
Sep 16, 2025
-
Electron Dot Notation For Aluminum
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Greater Than 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.