Is 0.02 Greater Than 0.03
seoindie
Sep 17, 2025 · 6 min read
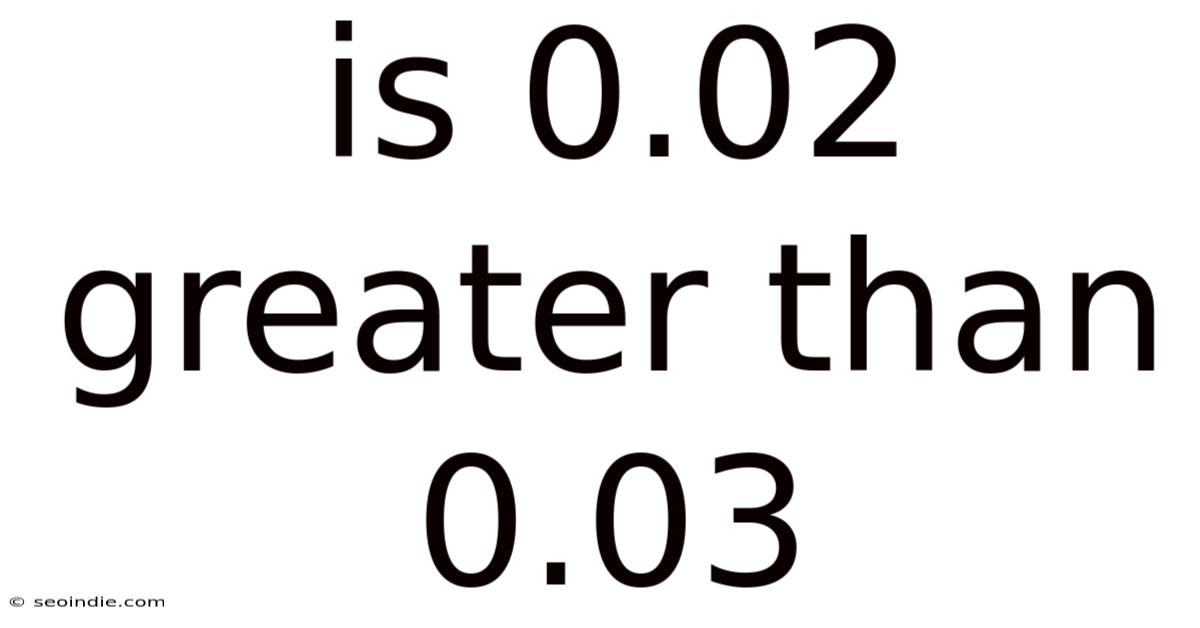
Table of Contents
Is 0.02 Greater Than 0.03? Understanding Decimal Place Value
This seemingly simple question, "Is 0.02 greater than 0.03?", often trips up students grappling with decimal place value. Understanding decimals is crucial for various aspects of mathematics and everyday life, from calculating finances to comprehending scientific data. This article will not only definitively answer the question but will also delve into a comprehensive explanation of decimal place value, providing a solid foundation for understanding decimal comparisons and operations.
Introduction: Deciphering the Decimal System
The decimal system, also known as the base-10 system, is the foundation of our number system. It's characterized by the use of ten digits (0-9) and a place value system where the position of a digit determines its value. Whole numbers are straightforward; each position represents a power of 10 (ones, tens, hundreds, and so on). Decimals extend this system to represent values less than one.
The decimal point separates the whole number part from the fractional part. To the right of the decimal point, each place represents a decreasing power of 10: tenths (1/10), hundredths (1/100), thousandths (1/1000), and so on. Understanding this place value is key to comparing and ordering decimals correctly.
Understanding Place Value in Decimals
Let's break down the numbers 0.02 and 0.03 to understand their values:
-
0.02: This number represents zero ones, zero tenths, and two hundredths. We can also express it as 2/100 or 1/50.
-
0.03: This number represents zero ones, zero tenths, and three hundredths. We can also express it as 3/100.
Comparing 0.02 and 0.03
Now, let's directly address the initial question: Is 0.02 greater than 0.03? The answer is no. 0.02 is less than 0.03.
To understand why, let's visualize it:
Imagine dividing a whole into 100 equal parts. 0.02 represents 2 of those 100 parts, while 0.03 represents 3 of those 100 parts. Clearly, 3 parts are more than 2 parts. Therefore, 0.03 > 0.02.
Step-by-Step Comparison of Decimals
Comparing decimals involves a systematic approach:
-
Align the decimal points: Write the numbers vertically, ensuring the decimal points are aligned. This helps you compare the digits in the same place value.
-
Compare digits from left to right: Start with the digit in the leftmost position (the largest place value). If the digits are different, the number with the larger digit in that position is the larger number.
-
Continue comparing: If the digits in a place value are the same, move to the next digit to the right and repeat the comparison.
Let's apply this to 0.02 and 0.03:
0.02
0.03
The digits in the ones place are both 0. Moving to the tenths place, they are both 0. Finally, in the hundredths place, we find 2 and 3. Since 3 > 2, we conclude that 0.03 > 0.02.
Illustrative Examples: Comparing Different Decimals
Let's consider some more examples to solidify your understanding:
-
Is 0.2 greater than 0.02? Yes. 0.2 is equivalent to 20 hundredths (0.20), which is greater than 2 hundredths (0.02).
-
Is 0.15 greater than 0.125? Yes. Comparing the tenths place, both are 1. In the hundredths place, 5 > 2, so 0.15 > 0.125.
-
Is 2.5 greater than 2.499? Yes. Although 2.499 appears close to 2.5, the tenths place determines the larger value. Since 5 > 4, 2.5 > 2.499.
Expanding the Concept: Working with Larger Decimals
The same principles apply when comparing decimals with more digits or whole number components:
-
Compare 12.345 and 12.346: The ones and tenths places are identical. In the hundredths place, they are also identical. However, in the thousandths place, 6 > 5, so 12.346 > 12.345.
-
Compare 35.78 and 35.780: These numbers are equal. Adding trailing zeros to the right of the decimal point does not change the value of the number.
The Significance of Zeroes in Decimals
Zeroes play a crucial role in decimals, especially when comparing numbers:
-
Leading zeroes: Zeroes to the left of the first non-zero digit in the fractional part are insignificant. 0.02 is the same as 0.02000; the added zeroes don't change the value.
-
Trailing zeroes: Zeroes to the right of the last non-zero digit after the decimal point are also insignificant. 0.2 is equal to 0.20 and 0.200.
However, zeroes are significant when they are between non-zero digits or before the decimal point. 0.002 is different than 0.2 and 2.0
Common Mistakes to Avoid When Comparing Decimals
Many mistakes stem from misunderstandings about place value:
-
Ignoring the decimal point: Treating decimals as whole numbers leads to incorrect comparisons.
-
Misinterpreting leading or trailing zeroes: Incorrectly assuming that adding or removing zeroes changes the value.
-
Focusing on the number of digits: A number with more digits isn't necessarily larger. 0.0001 is less than 0.1.
Scientific Notation and Decimal Comparisons
For extremely large or small numbers, scientific notation is used. Comparing numbers in scientific notation involves comparing the exponents and then the mantissas. A larger exponent indicates a larger number. If the exponents are the same, compare the mantissas.
Conclusion: Mastering Decimal Comparisons
Comparing decimals might seem trivial at first glance, but it's a fundamental skill crucial for various mathematical and real-world applications. This article has provided a thorough breakdown of decimal place value and outlined a step-by-step method for accurate comparison. By understanding the importance of place value and avoiding common pitfalls, you can confidently compare any decimals and build a stronger foundation in mathematics. Remember, the key is to systematically compare digits from left to right, paying close attention to the position of each digit relative to the decimal point.
Frequently Asked Questions (FAQ)
-
Q: How do I convert a fraction to a decimal? A: Divide the numerator by the denominator. For example, 1/4 = 1 ÷ 4 = 0.25.
-
Q: How do I convert a decimal to a fraction? A: Write the decimal as a fraction with a denominator that is a power of 10 (10, 100, 1000, etc.), depending on the number of digits after the decimal point. Then, simplify the fraction. For example, 0.25 = 25/100 = 1/4.
-
Q: What if the decimals have different numbers of digits after the decimal point? A: Add trailing zeros to the shorter decimal to make both have the same number of digits after the decimal point. This doesn't change the value, but it makes the comparison easier.
-
Q: Can I use a calculator to compare decimals? A: Yes, calculators can help with comparisons, but understanding the underlying principles is still crucial for accurate and efficient problem-solving.
This comprehensive guide should equip you with the necessary knowledge and skills to confidently tackle any decimal comparison task. Remember to practice regularly to solidify your understanding and build your mathematical proficiency.
Latest Posts
Latest Posts
-
Hcf Of 36 And 84
Sep 17, 2025
-
How To Describe A Book
Sep 17, 2025
-
Right Triangle Moment Of Inertia
Sep 17, 2025
-
128 In Simplest Radical Form
Sep 17, 2025
-
Para Military Forces In India
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Is 0.02 Greater Than 0.03 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.