Integral Of 1 X 3
seoindie
Sep 14, 2025 · 6 min read
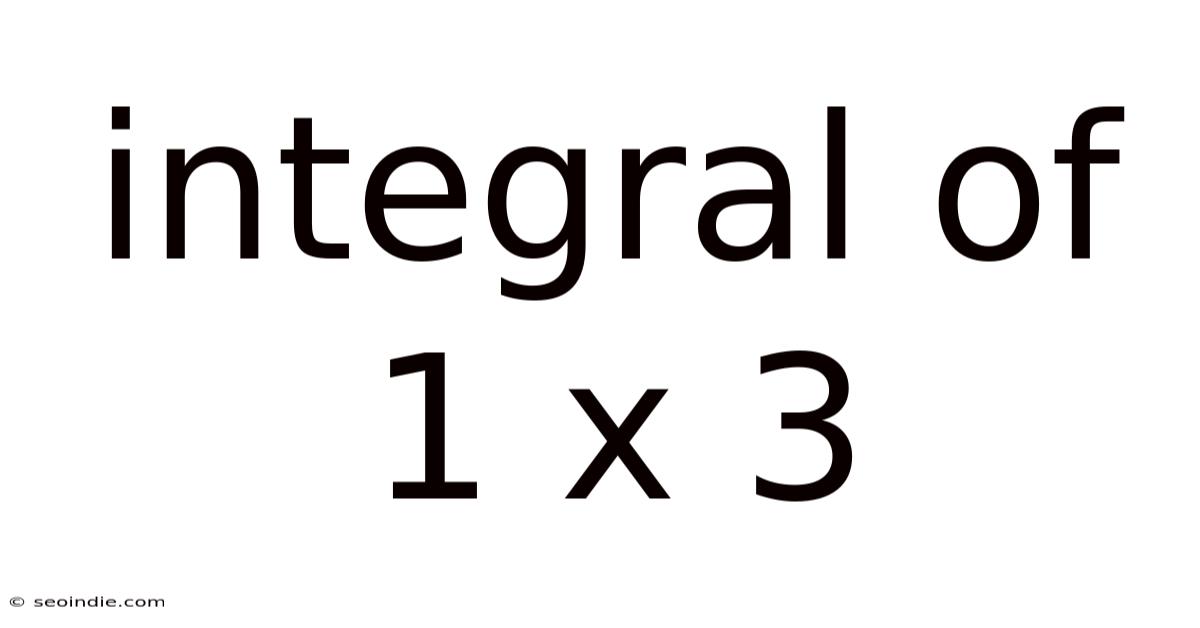
Table of Contents
Understanding and Solving the Integral of 1/(x³): A Comprehensive Guide
The integral of 1/x³, often written as ∫(1/x³)dx, is a fundamental concept in calculus. This seemingly simple integral presents a great opportunity to delve into the core principles of integration, power rules, and the handling of negative exponents. This article will guide you through the process of solving this integral, explain the underlying mathematical concepts, and address frequently asked questions. We'll break down the solution step-by-step, making it accessible to students of all levels, from beginners grappling with the basics to those aiming to solidify their understanding of integration techniques.
Introduction to Integration
Before diving into the specific integral, let's briefly review the concept of integration. Integration is essentially the reverse process of differentiation. Where differentiation finds the instantaneous rate of change of a function, integration finds the area under the curve of a function. This area represents the accumulation of the function's values over a given interval. We use the symbol ∫ (an elongated "S," representing "sum") to denote integration. The "dx" indicates that we are integrating with respect to the variable 'x'.
There are two main types of integrals: definite and indefinite. A definite integral has defined limits of integration, providing a numerical result representing the exact area under the curve between those limits. An indefinite integral, on the other hand, represents a family of functions whose derivatives are equal to the integrand. It includes a constant of integration (+C) to account for the fact that many functions can have the same derivative. The integral of 1/x³ is an indefinite integral because we are not given specific limits of integration.
Solving the Integral: ∫(1/x³)dx
Now, let's tackle the integral at hand: ∫(1/x³)dx. The key to solving this integral lies in rewriting the integrand using negative exponents. Recall that 1/x³ is equivalent to x⁻³. Therefore, our integral becomes:
∫x⁻³ dx
Now, we can apply the power rule of integration. The power rule states that the integral of xⁿ is (xⁿ⁺¹)/(n+1) + C, where 'n' is any real number except -1, and 'C' is the constant of integration.
Applying the power rule to our integral:
∫x⁻³ dx = (x⁻³⁺¹)/(-3+1) + C
Simplifying the exponent:
= (x⁻²)/(-2) + C
Finally, rewriting the expression without negative exponents:
= -1/(2x²) + C
Therefore, the integral of 1/x³ is -1/(2x²) + C. The constant of integration, 'C', is crucial because any constant added to this function will have the same derivative (1/x³).
A Deeper Dive into the Power Rule and its Limitations
The power rule of integration is a fundamental tool in calculus, but it has limitations. It's vital to understand these limitations to avoid common mistakes. The power rule, as stated earlier, is:
∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C (where n ≠ -1)
The restriction "n ≠ -1" is critical. If n = -1, the denominator becomes zero, resulting in an undefined expression. This is why the integral of 1/x (x⁻¹) is not solved using the power rule directly; it results in ln|x| + C (the natural logarithm of the absolute value of x).
The integral of 1/x³ avoids this specific issue because the exponent (-3) is not equal to -1. However, understanding the exception to the power rule is crucial for tackling other integrals.
Visualizing the Integral with Geometry
While the algebraic solution provides the precise answer, visualizing the integral can enhance understanding. The integral represents the area under the curve y = 1/x³. This curve is a hyperbola, decreasing rapidly as x increases. The area under this curve is, of course, negative for positive values of x because the curve lies below the x-axis. The negative sign in our solution (-1/(2x²) + C) reflects this negative area.
The constant of integration, 'C', represents a vertical shift of the antiderivative. It signifies that multiple functions could have the same derivative; they are all simply vertical translations of each other. This is a crucial concept to grasp when dealing with indefinite integrals.
Step-by-Step Solution with Detailed Explanation
To solidify understanding, let's reiterate the step-by-step solution with a more detailed explanation of each step:
-
Rewrite the Integrand: The initial integral is ∫(1/x³)dx. We rewrite this using negative exponents: ∫x⁻³dx. This simplification makes it easier to apply the power rule.
-
Apply the Power Rule: The power rule for integration states ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C. Substituting n = -3 into the power rule gives us: (x⁻³⁺¹)/(-3+1) + C.
-
Simplify the Exponent: Simplifying the exponent, we get (x⁻²)/(-2) + C. This step involves basic arithmetic with exponents.
-
Rewrite without Negative Exponents: Finally, we rewrite the expression without negative exponents to obtain the standard form: -1/(2x²) + C. This makes the result easier to interpret and use in further calculations.
Common Mistakes to Avoid
Several common mistakes can arise when solving integrals like ∫(1/x³)dx. Let's address some of them:
-
Incorrect application of the power rule: Forgetting to add 1 to the exponent and divide by the new exponent is a frequent error. Double-check your arithmetic in this step.
-
Neglecting the constant of integration (C): Always remember to include the constant of integration (+C) in the solution for indefinite integrals. This constant represents a family of functions, all with the same derivative.
-
Incorrect handling of negative exponents: Ensure you understand the rules of working with negative exponents. Mistakes in this area can lead to an incorrect final answer.
-
Confusing integration with differentiation: Integration and differentiation are reverse operations. Do not confuse the rules of one with the rules of the other.
Frequently Asked Questions (FAQ)
Q: What is the difference between a definite and an indefinite integral?
A: A definite integral has limits of integration (e.g., ∫(from a to b) f(x) dx), giving a numerical value representing the area under the curve between those limits. An indefinite integral does not have limits, resulting in a family of functions (plus the constant of integration, C).
Q: Why is the constant of integration (+C) necessary?
A: The derivative of a constant is zero. Therefore, many functions can have the same derivative. The constant of integration accounts for this ambiguity, representing the entire family of functions that could produce the original integrand upon differentiation.
Q: Can this integral be solved using other methods?
A: While the power rule is the most straightforward method for this specific integral, other integration techniques exist (like substitution or integration by parts) for more complex integrals. However, for ∫(1/x³)dx, the power rule is the most efficient and accurate approach.
Q: What are some real-world applications of this type of integral?
A: Integrals of this form appear in various applications of physics and engineering. For instance, they might model the rate of decay of a radioactive substance or aspects of electrical circuits.
Conclusion
Solving the integral of 1/x³ involves a straightforward application of the power rule of integration. However, understanding the underlying principles of integration, the power rule’s limitations, and the significance of the constant of integration are crucial for mastering calculus. By carefully following the steps outlined above and avoiding common pitfalls, you can confidently solve this and similar integrals. Remember to always check your work and, most importantly, practice consistently to build a solid foundation in integral calculus. This fundamental understanding will serve you well as you progress to more complex integration techniques and applications.
Latest Posts
Latest Posts
-
Picture Of A Cell Wall
Sep 14, 2025
-
What The Properties Of Metals
Sep 14, 2025
-
How Much Is A 3rd
Sep 14, 2025
-
Gcf Of 32 And 28
Sep 14, 2025
-
How To Do Base Division
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.