Hcf Of 8 And 12
seoindie
Sep 15, 2025 · 6 min read
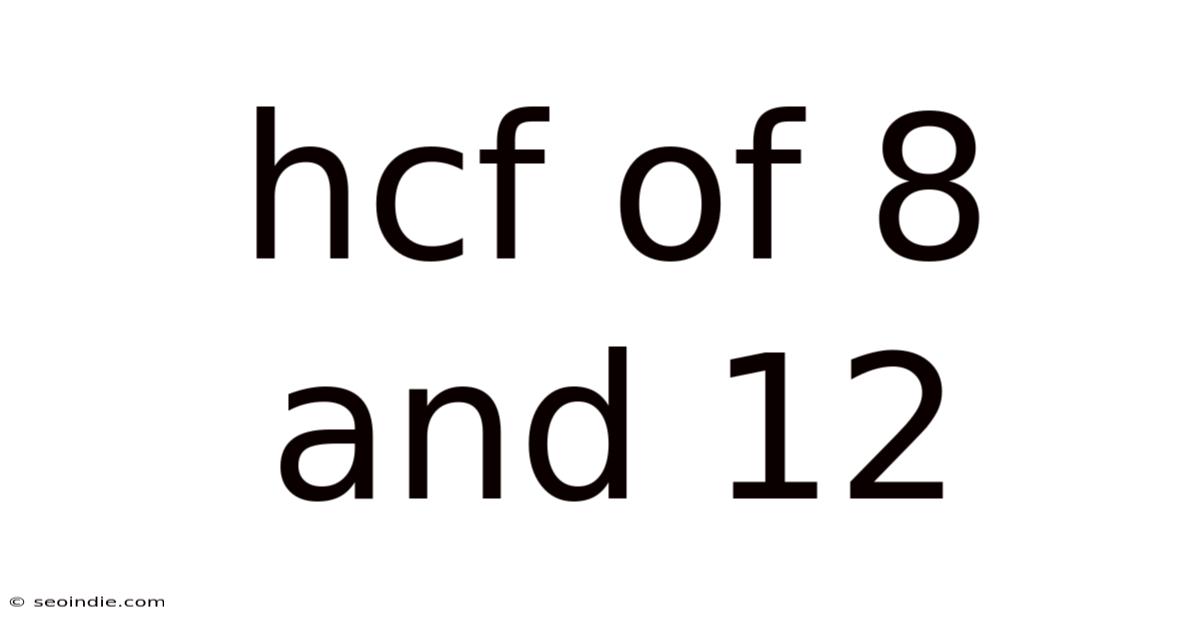
Table of Contents
Unveiling the Secrets of HCF: A Deep Dive into the Highest Common Factor of 8 and 12
Finding the highest common factor (HCF), also known as the greatest common divisor (GCD), is a fundamental concept in mathematics. Understanding HCF is crucial for simplifying fractions, solving problems related to measurement, and laying the groundwork for more advanced mathematical concepts. This article will delve into the HCF of 8 and 12, explaining various methods to calculate it, exploring its real-world applications, and addressing common questions surrounding this essential mathematical operation. By the end, you'll not only know the HCF of 8 and 12 but also possess a comprehensive understanding of the concept itself.
Understanding Highest Common Factor (HCF)
The highest common factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. In simpler terms, it's the biggest number that's a factor of all the numbers involved. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The highest of these common factors is 6, therefore the HCF of 12 and 18 is 6.
Calculating the HCF of 8 and 12: Multiple Methods
There are several effective ways to calculate the HCF, each with its own advantages. Let's explore three common methods:
1. Prime Factorization Method
This method involves finding the prime factors of each number and then identifying the common prime factors raised to the lowest power.
- Prime factorization of 8: 8 = 2 x 2 x 2 = 2³
- Prime factorization of 12: 12 = 2 x 2 x 3 = 2² x 3
The common prime factor is 2. The lowest power of 2 present in both factorizations is 2². Therefore, the HCF of 8 and 12 is 2².
HCF(8, 12) = 2² = 4
2. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 8: 1, 2, 4, 8
- Factors of 12: 1, 2, 3, 4, 6, 12
The common factors of 8 and 12 are 1, 2, and 4. The highest common factor is 4.
HCF(8, 12) = 4
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the HCF, especially when dealing with larger numbers. It's based on the principle that the HCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
- Start with the larger number (12) and the smaller number (8).
- Divide the larger number by the smaller number and find the remainder: 12 ÷ 8 = 1 with a remainder of 4.
- Replace the larger number (12) with the smaller number (8) and the smaller number (8) with the remainder (4).
- Repeat the process: 8 ÷ 4 = 2 with a remainder of 0.
- Since the remainder is 0, the HCF is the last non-zero remainder, which is 4.
HCF(8, 12) = 4
Real-World Applications of HCF
The concept of HCF is not just a theoretical exercise; it has numerous practical applications in everyday life and various fields:
-
Simplifying Fractions: Finding the HCF of the numerator and denominator allows us to simplify fractions to their lowest terms. For example, the fraction 12/8 can be simplified to 3/2 by dividing both the numerator and the denominator by their HCF, which is 4.
-
Measurement and Division: HCF is useful when dealing with problems involving measurements and divisions. Imagine you have two pieces of ribbon, one 8 inches long and the other 12 inches long. You want to cut them into smaller pieces of equal length without any waste. The HCF (4 inches) will give you the length of the largest possible pieces you can cut.
-
Arranging Objects in Rows and Columns: Suppose you have 8 red marbles and 12 blue marbles. You want to arrange them in rows with the same number of marbles in each row, using all the marbles. The HCF (4) tells you that you can arrange them in 4 rows, with 2 red marbles and 3 blue marbles in each row.
-
Data Analysis and Pattern Recognition: In data analysis, the HCF can help identify patterns and common factors within datasets, potentially revealing hidden relationships or structures.
Beyond the Basics: Extending the HCF Concept
The HCF concept extends beyond just two numbers. You can find the HCF of three or more numbers using the same methods discussed earlier. For example, to find the HCF of 8, 12, and 16, you would first find the prime factorization of each number:
- 8 = 2³
- 12 = 2² x 3
- 16 = 2⁴
The common prime factor is 2, and the lowest power is 2², therefore the HCF(8, 12, 16) = 4.
The Euclidean algorithm can also be extended to find the HCF of more than two numbers. You would find the HCF of two numbers first, and then find the HCF of the result and the next number, and so on.
Frequently Asked Questions (FAQ)
Q: What happens if the HCF of two numbers is 1?
A: If the HCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
Q: Can the HCF of two numbers be greater than the smaller number?
A: No. The HCF of two numbers can never be greater than the smaller of the two numbers.
Q: Is there a way to find the HCF of very large numbers?
A: While the prime factorization method and the listing factors method become impractical for very large numbers, the Euclidean algorithm remains highly efficient even for large numbers, making it the preferred method in such cases. Computational tools and software can further assist with calculating HCF for extremely large numbers.
Q: What is the difference between HCF and LCM?
A: The HCF (Highest Common Factor) is the largest number that divides both numbers without leaving a remainder. The LCM (Least Common Multiple) is the smallest number that is a multiple of both numbers. They are closely related concepts, and their product is equal to the product of the two original numbers. For example, for 8 and 12, HCF(8, 12) = 4 and LCM(8, 12) = 24. Notice that 4 x 24 = 96, and 8 x 12 = 96.
Conclusion: Mastering the HCF
Understanding the HCF is a cornerstone of number theory and has wide-ranging applications in various fields. Through different methods like prime factorization, listing factors, and the Euclidean algorithm, we can efficiently determine the HCF of any set of numbers. The ability to calculate HCF empowers us to solve diverse practical problems and deepen our understanding of fundamental mathematical principles. Remember to choose the method that best suits the numbers involved and the context of the problem you're trying to solve. By mastering the HCF, you are building a strong foundation for more advanced mathematical explorations.
Latest Posts
Latest Posts
-
What Times What Is 40
Sep 15, 2025
-
Five Examples Of Biotic Factors
Sep 15, 2025
-
Minerals Can Be Divided Into
Sep 15, 2025
-
List The Factors Of 4
Sep 15, 2025
-
Is Polar Negative Or Positive
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 8 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.