Hcf Of 20 And 30
seoindie
Sep 11, 2025 · 6 min read
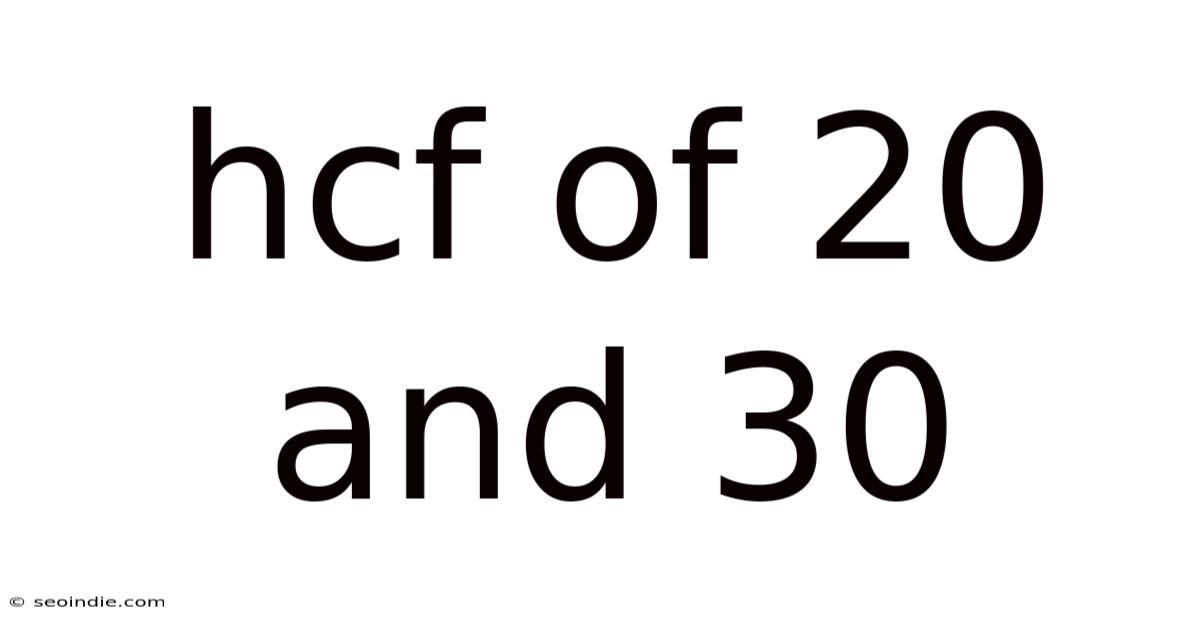
Table of Contents
Unveiling the Secrets of HCF: A Deep Dive into the Highest Common Factor of 20 and 30
Finding the highest common factor (HCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. But understanding the underlying principles and various methods for calculating the HCF opens up a fascinating world of number theory. This article will delve deep into finding the HCF of 20 and 30, exploring different approaches and demonstrating their applications beyond simple calculations. We'll uncover why understanding HCF is crucial in various mathematical concepts and problem-solving scenarios.
Understanding the Concept of Highest Common Factor (HCF)
The highest common factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. In simpler terms, it's the biggest number that's a factor of all the given numbers. For instance, the factors of 20 are 1, 2, 4, 5, 10, and 20. The factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30. The common factors of 20 and 30 are 1, 2, 5, and 10. The highest among these common factors is 10. Therefore, the HCF of 20 and 30 is 10.
This seemingly straightforward concept has significant applications in various mathematical fields, including simplifying fractions, solving algebraic equations, and understanding the relationships between numbers.
Method 1: Prime Factorization Method
This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this to find the HCF of 20 and 30:
Step 1: Prime Factorization of 20
20 = 2 x 2 x 5 = 2² x 5
Step 2: Prime Factorization of 30
30 = 2 x 3 x 5
Step 3: Identifying Common Prime Factors
Both 20 and 30 share the prime factors 2 and 5.
Step 4: Calculating the HCF
Multiply the common prime factors together: 2 x 5 = 10.
Therefore, the HCF of 20 and 30 using the prime factorization method is 10. This method is particularly helpful for understanding the fundamental structure of numbers and their relationships.
Method 2: Listing Factors Method
This method is straightforward, especially for smaller numbers. It involves listing all the factors of each number and then identifying the common factors.
Step 1: List the Factors of 20
Factors of 20: 1, 2, 4, 5, 10, 20
Step 2: List the Factors of 30
Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
Step 3: Identify Common Factors
Common factors of 20 and 30: 1, 2, 5, 10
Step 4: Determine the Highest Common Factor
The highest common factor among these is 10.
Therefore, the HCF of 20 and 30 using the listing factors method is 10. While simple, this method becomes less efficient when dealing with larger numbers.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the HCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the HCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the HCF.
Let's apply the Euclidean algorithm to find the HCF of 20 and 30:
Step 1: Subtract the smaller number from the larger number
30 - 20 = 10
Step 2: Replace the larger number with the result
Now we have the numbers 10 and 20.
Step 3: Repeat the process
20 - 10 = 10
Now we have the numbers 10 and 10. Since both numbers are equal, the HCF is 10.
Therefore, the HCF of 20 and 30 using the Euclidean algorithm is 10. This method is significantly more efficient than the previous methods when dealing with larger numbers.
The Significance of HCF in Mathematics and Beyond
The concept of HCF extends far beyond simple arithmetic exercises. Its applications are crucial in various mathematical areas and real-world scenarios:
-
Simplifying Fractions: To simplify a fraction to its lowest terms, we divide both the numerator and denominator by their HCF. For example, the fraction 20/30 can be simplified to 2/3 by dividing both the numerator and denominator by their HCF, which is 10.
-
Solving Algebraic Equations: HCF plays a vital role in solving certain types of algebraic equations, particularly those involving polynomial expressions. Finding the HCF of the terms in an equation often helps in simplifying and solving the equation.
-
Measurement and Geometry: HCF is used to determine the largest possible square tile that can be used to cover a rectangular floor without any cuts or gaps. The dimensions of the floor are divided by their HCF to find the number of tiles needed.
-
Number Theory: HCF is a fundamental concept in number theory, a branch of mathematics concerned with the properties of integers. It is crucial in understanding divisibility rules, prime numbers, and other related concepts.
HCF and LCM: A Complementary Relationship
The highest common factor (HCF) and the least common multiple (LCM) are closely related concepts. The LCM of two numbers is the smallest number that is a multiple of both numbers. For the numbers 20 and 30, the LCM is 60. There's a fascinating relationship between the HCF and LCM of two numbers (a and b):
a x b = HCF(a, b) x LCM(a, b)
Using this formula for 20 and 30:
20 x 30 = 600
10 (HCF) x 60 (LCM) = 600
This relationship highlights the interconnectedness of these two important concepts in number theory.
Frequently Asked Questions (FAQ)
Q1: What is the difference between HCF and GCD?
A1: HCF (Highest Common Factor) and GCD (Greatest Common Divisor) are essentially the same thing. They both refer to the largest number that divides two or more numbers without leaving a remainder.
Q2: Can the HCF of two numbers be 1?
A2: Yes, if two numbers are relatively prime or coprime, meaning they have no common factors other than 1, their HCF is 1. For example, the HCF of 15 and 28 is 1.
Q3: How do I find the HCF of more than two numbers?
A3: You can extend any of the methods discussed (prime factorization, listing factors, or Euclidean algorithm) to find the HCF of more than two numbers. For instance, using prime factorization, you would find the prime factorization of each number and then identify the common prime factors to the lowest power.
Q4: Why is the Euclidean Algorithm more efficient for larger numbers?
A4: The Euclidean Algorithm avoids the need to find all factors, which can be computationally expensive for large numbers. Its iterative subtraction process quickly reduces the numbers to their HCF.
Conclusion: Mastering the Art of Finding HCF
Understanding the highest common factor is a foundational skill in mathematics. This article has explored three different methods – prime factorization, listing factors, and the Euclidean algorithm – for calculating the HCF, highlighting the strengths and weaknesses of each approach. We've also emphasized the broader significance of HCF in various mathematical contexts and real-world applications. By mastering these methods and grasping the underlying principles, you'll be well-equipped to tackle more complex mathematical problems and appreciate the beauty and elegance of number theory. Remember, the journey of learning is ongoing, and each new concept builds upon the previous ones, paving the way for a deeper understanding of the mathematical world.
Latest Posts
Latest Posts
-
Words With Second Letter E
Sep 11, 2025
-
2 Letter Words With A
Sep 11, 2025
-
What Is 72 Divisible By
Sep 11, 2025
-
Energy Of Activation Definition Chemistry
Sep 11, 2025
-
What Is A Vegetative Cell
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 20 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.