Gcf Of 40 And 72
seoindie
Sep 18, 2025 · 6 min read
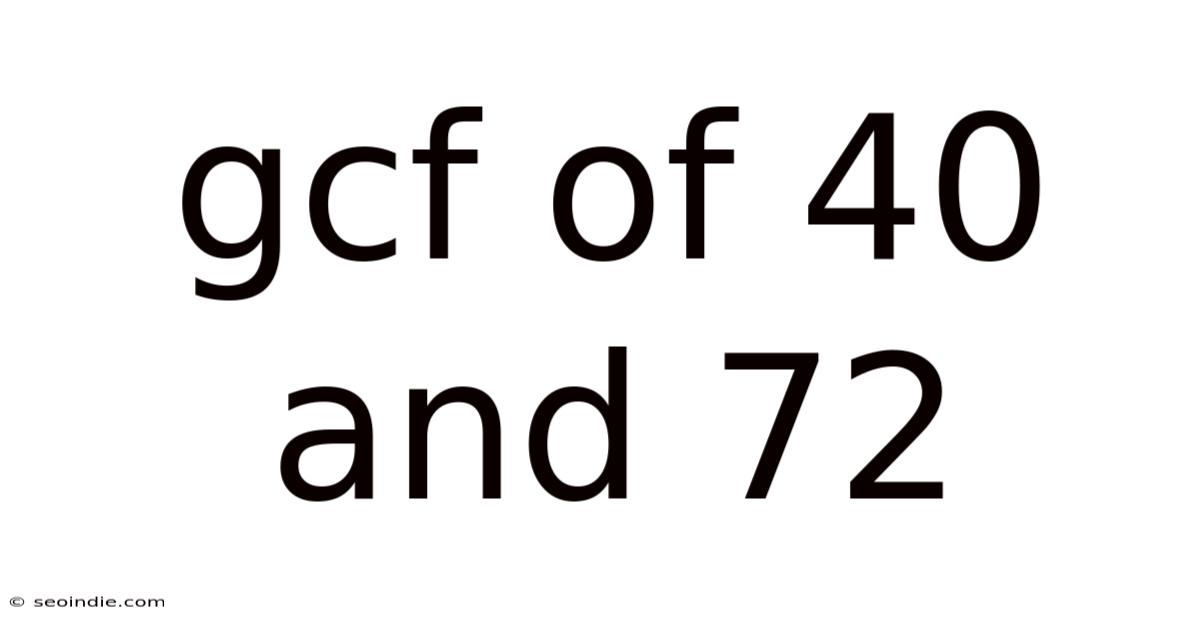
Table of Contents
Finding the Greatest Common Factor (GCF) of 40 and 72: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will delve deep into the process of determining the GCF of 40 and 72, exploring various methods, providing detailed explanations, and extending the understanding beyond a simple answer. We'll cover everything from the basic methods suitable for beginners to more advanced techniques, making this a comprehensive guide for anyone looking to master GCF calculations.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all of the numbers without leaving a remainder. It represents the largest common divisor shared by the numbers. Understanding the GCF is crucial in various mathematical applications, including simplifying fractions, solving algebraic equations, and understanding number theory concepts. Let's focus on finding the GCF of 40 and 72.
Method 1: Prime Factorization
This method is considered one of the most reliable and widely understood techniques for finding the GCF. It involves breaking down each number into its prime factors—numbers divisible only by 1 and themselves.
Step 1: Prime Factorization of 40
40 can be factored as follows:
40 = 2 x 20 = 2 x 2 x 10 = 2 x 2 x 2 x 5 = 2³ x 5¹
Therefore, the prime factorization of 40 is 2³ x 5¹.
Step 2: Prime Factorization of 72
72 can be factored as follows:
72 = 2 x 36 = 2 x 2 x 18 = 2 x 2 x 2 x 9 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
Therefore, the prime factorization of 72 is 2³ x 3².
Step 3: Identifying Common Factors
Now, compare the prime factorizations of 40 and 72:
40 = 2³ x 5¹ 72 = 2³ x 3²
We can see that both numbers share three factors of 2.
Step 4: Calculating the GCF
The GCF is the product of the common prime factors raised to the lowest power they appear in either factorization. In this case, the only common prime factor is 2, and the lowest power it appears in is 2³.
GCF(40, 72) = 2³ = 8
Therefore, the greatest common factor of 40 and 72 is 8.
Method 2: Listing Factors
This method is more suitable for smaller numbers. It involves listing all the factors of each number and then identifying the largest common factor.
Step 1: Listing Factors of 40
The factors of 40 are: 1, 2, 4, 5, 8, 10, 20, 40
Step 2: Listing Factors of 72
The factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Step 3: Identifying Common Factors
Comparing the lists, we find the common factors: 1, 2, 4, 8.
Step 4: Determining the GCF
The largest common factor is 8.
Therefore, the greatest common factor of 40 and 72 is 8. While this method is straightforward, it becomes less efficient with larger numbers.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Step 1: Repeated Subtraction
Let's start with 72 and 40:
72 - 40 = 32
Now, we replace 72 with 32:
40 - 32 = 8
Now, we replace 40 with 8:
32 - 8 = 24
Now, we replace 32 with 24:
24 - 8 = 16
Now, we replace 24 with 16:
16 - 8 = 8
Now, we replace 16 with 8:
8 - 8 = 0
Since we've reached 0, the GCF is the last non-zero remainder, which is 8.
Step 2: Division-Based Euclidean Algorithm (More Efficient)
The repeated subtraction can be streamlined using division:
Divide 72 by 40: 72 = 40 x 1 + 32 (The remainder is 32) Divide 40 by 32: 40 = 32 x 1 + 8 (The remainder is 8) Divide 32 by 8: 32 = 8 x 4 + 0 (The remainder is 0)
The last non-zero remainder is 8, therefore the GCF(40,72) = 8. This division-based approach is much more efficient than repeated subtraction, especially for larger numbers.
Applications of GCF
The GCF finds practical applications in various areas:
-
Simplifying Fractions: To simplify a fraction, divide both the numerator and denominator by their GCF. For example, the fraction 40/72 can be simplified to 5/9 by dividing both by their GCF, 8.
-
Solving Algebraic Equations: The GCF is used in factoring expressions, a crucial step in solving many algebraic equations.
-
Geometry: The GCF can be applied in problems related to finding the largest square tile that can perfectly cover a rectangular area.
-
Number Theory: GCF is a fundamental concept in number theory, playing a crucial role in various theorems and proofs.
Beyond 40 and 72: Extending the Concepts
The methods described above can be applied to find the GCF of any two numbers. For instance, let's find the GCF of 108 and 144 using the prime factorization method:
108 = 2² x 3³ 144 = 2⁴ x 3²
The common prime factors are 2² and 3². Therefore, the GCF(108, 144) = 2² x 3² = 4 x 9 = 36.
Finding the GCF of more than two numbers involves a similar process. You would find the prime factorization of each number and identify the common prime factors raised to their lowest powers.
Frequently Asked Questions (FAQ)
Q1: What if the GCF of two numbers is 1?
A1: If the GCF of two numbers is 1, it means the numbers are relatively prime or coprime. They don't share any common factors other than 1.
Q2: Can the GCF be larger than either of the numbers?
A2: No. The GCF can never be larger than the smaller of the two numbers.
Q3: Is there a limit to the size of numbers for which we can find the GCF?
A3: Theoretically, there's no limit. While manual methods might become tedious for extremely large numbers, computer algorithms can efficiently calculate the GCF of arbitrarily large numbers.
Q4: Which method is the most efficient?
A4: For larger numbers, the Euclidean algorithm (especially the division-based version) is significantly more efficient than listing factors or prime factorization. Prime factorization becomes less efficient as the numbers get larger and more complex.
Conclusion
Finding the greatest common factor is a valuable skill with applications across various mathematical domains. We've explored three different methods: prime factorization, listing factors, and the Euclidean algorithm, each with its own strengths and weaknesses. Understanding these methods equips you not only to calculate the GCF but also to grasp the underlying mathematical principles. Remember to choose the method most appropriate for the size and complexity of the numbers involved. The GCF of 40 and 72, as demonstrated, is 8, a result achievable using any of the methods outlined above. Mastering this concept opens doors to a deeper understanding of number theory and its numerous applications.
Latest Posts
Latest Posts
-
How Long Is 6 Inches
Sep 18, 2025
-
Unit Of Measurement For Heat
Sep 18, 2025
-
How To Determine Atomic Radius
Sep 18, 2025
-
All Factor Pairs To 80
Sep 18, 2025
-
Ways To Describe Blue Eyes
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 40 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.