Gcf Of 36 And 81
seoindie
Sep 18, 2025 · 6 min read
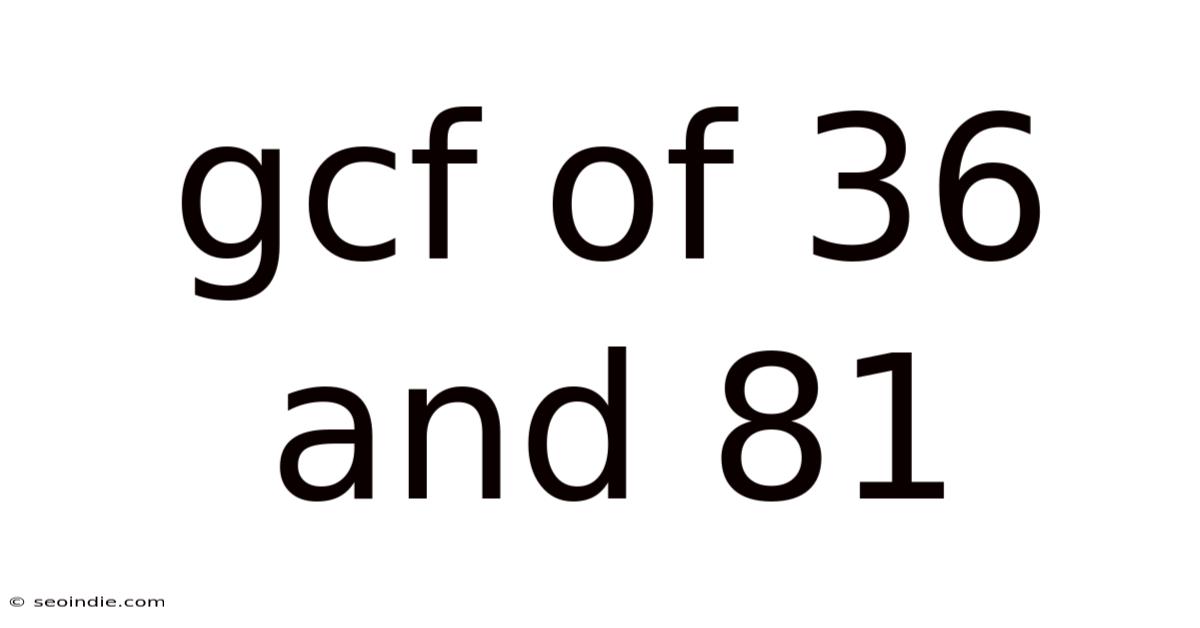
Table of Contents
Finding the Greatest Common Factor (GCF) of 36 and 81: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will provide a thorough explanation of how to find the GCF of 36 and 81, exploring various methods and delving into the underlying mathematical principles. Understanding GCFs is crucial for simplifying fractions, solving algebraic equations, and many other mathematical operations. This guide will equip you with the knowledge and skills to confidently calculate the GCF of any two numbers, regardless of their size.
Understanding Greatest Common Factor (GCF)
Before we dive into calculating the GCF of 36 and 81, let's establish a clear understanding of what a GCF is. The GCF of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, so the GCF of 12 and 18 is 6.
Method 1: Listing Factors
This is a straightforward method, particularly effective for smaller numbers like 36 and 81. Let's begin by listing all the factors of each number:
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 81: 1, 3, 9, 27, 81
Now, compare the two lists and identify the common factors: 1, 3, and 9. The greatest of these common factors is 9.
Therefore, the GCF of 36 and 81 is $\boxed{9}$.
Method 2: Prime Factorization
Prime factorization is a more powerful method, especially useful for larger numbers. This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Prime factorization of 36:
36 = 2 x 18 = 2 x 2 x 9 = 2 x 2 x 3 x 3 = 2² x 3²
Prime factorization of 81:
81 = 3 x 27 = 3 x 3 x 9 = 3 x 3 x 3 x 3 = 3⁴
Now, identify the common prime factors and their lowest powers: Both 36 and 81 contain the prime factor 3. The lowest power of 3 present in both factorizations is 3².
Therefore, the GCF of 36 and 81 is 3² = $\boxed{9}$.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially large ones. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 36 and 81:
- Start with the larger number (81) and the smaller number (36).
- Divide the larger number by the smaller number and find the remainder: 81 ÷ 36 = 2 with a remainder of 9.
- Replace the larger number with the smaller number (36) and the smaller number with the remainder (9).
- Repeat the process: 36 ÷ 9 = 4 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 9.
Therefore, the GCF of 36 and 81 is $\boxed{9}$.
Mathematical Explanation of the Methods
The methods above, while seemingly different, are all rooted in the fundamental theorems of arithmetic. The prime factorization method directly uses the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. By identifying the common prime factors and their lowest powers, we effectively find the largest number that divides both numbers evenly.
The Euclidean algorithm, though appearing more procedural, is implicitly based on the properties of divisibility. Each step in the algorithm maintains the invariant that the GCF remains unchanged. The process continues until the remainder becomes zero, at which point the last non-zero remainder is the GCF. This is a consequence of the properties of modular arithmetic and the division algorithm.
Applications of GCF
Understanding and calculating the GCF has numerous applications across various mathematical domains:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 36/81 can be simplified by dividing both the numerator and denominator by their GCF (9), resulting in the equivalent fraction 4/9.
-
Solving Algebraic Equations: GCFs are used in factoring polynomials, a crucial step in solving many algebraic equations.
-
Geometry and Measurement: GCF is used in solving problems related to area, volume, and other geometric concepts. For instance, finding the largest square tile that can perfectly cover a rectangular floor involves calculating the GCF of the floor's dimensions.
-
Number Theory: GCF is a cornerstone concept in number theory, forming the basis for many advanced theorems and algorithms.
-
Computer Science: The Euclidean algorithm, used for GCF calculation, is a highly efficient algorithm used in computer science for various applications, including cryptography.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, the numbers are called relatively prime or coprime. This means they share no common factors other than 1.
Q: Can the GCF of two numbers be larger than the smaller number?
A: No, the GCF of two numbers can never be larger than the smaller of the two numbers.
Q: Is there a limit to the size of numbers for which I can find the GCF?
A: Theoretically, there is no limit to the size of numbers for which you can find the GCF. However, for extremely large numbers, computational limitations might become a factor. The Euclidean algorithm remains an efficient method even for large numbers.
Q: Why is prime factorization a useful method for finding the GCF?
A: Prime factorization provides a unique representation of each number. By comparing these representations, we can directly identify the common factors and their lowest powers, which directly leads to the GCF.
Conclusion
Finding the greatest common factor (GCF) of 36 and 81, as demonstrated through various methods, is a fundamental mathematical skill with broad applications. Whether you use the method of listing factors, prime factorization, or the Euclidean algorithm, understanding the underlying principles ensures that you can confidently calculate the GCF of any pair of numbers. Mastering this concept opens doors to a deeper understanding of number theory and its practical applications in various fields. Remember that the GCF is not just a simple calculation; it's a key concept that unlocks a more profound understanding of the relationships between numbers. By understanding its different calculation methods and applications, you'll be well-equipped to tackle more complex mathematical problems in the future.
Latest Posts
Latest Posts
-
Sports That Begin With F
Sep 18, 2025
-
Words That End In Die
Sep 18, 2025
-
Words That End In Ble
Sep 18, 2025
-
Words That End With Tet
Sep 18, 2025
-
3000 Sq Ft In Metres
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 36 And 81 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.