Gcf Of 27 And 72
seoindie
Sep 23, 2025 · 6 min read
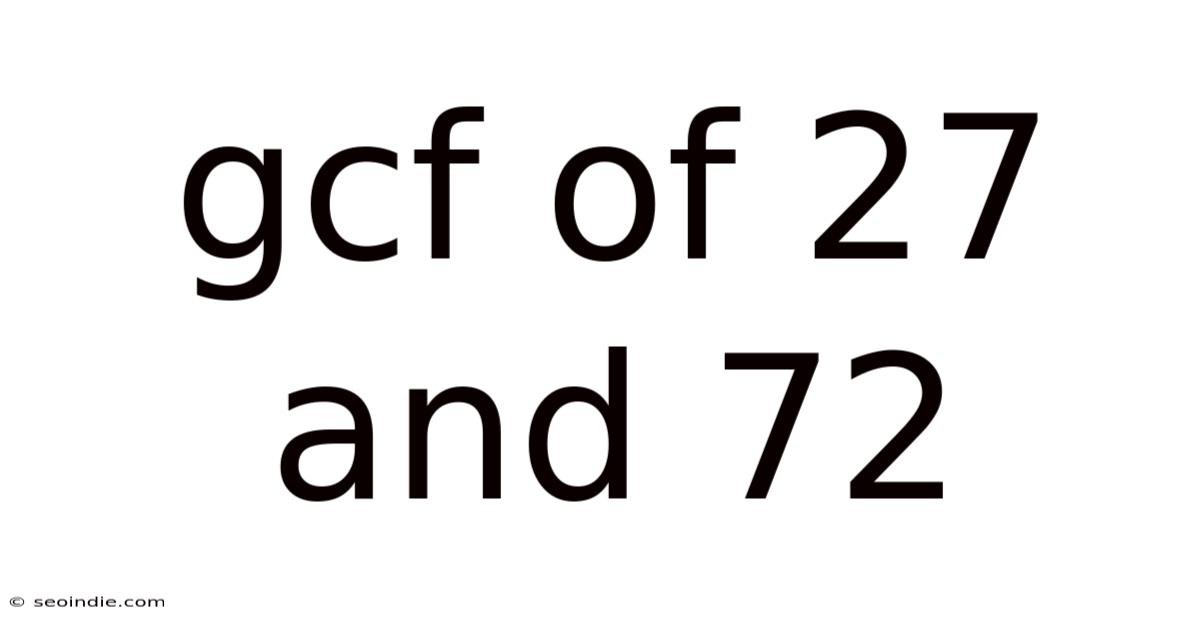
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 27 and 72: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications spanning various fields, from simplifying fractions to solving complex algebraic equations. This article provides a comprehensive exploration of how to determine the GCF of 27 and 72, utilizing several methods, and delving into the underlying mathematical principles. We'll cover different approaches, making this a valuable resource for students and anyone looking to deepen their understanding of number theory.
Introduction to Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. Understanding the GCF is crucial for simplifying fractions, factoring polynomials, and solving various mathematical problems. This article focuses on finding the GCF of 27 and 72, illustrating multiple methods to achieve this.
Method 1: Prime Factorization
Prime factorization is a powerful technique for finding the GCF. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves. Let's apply this method to find the GCF of 27 and 72:
1. Prime Factorization of 27:
27 can be broken down as follows:
27 = 3 x 9 = 3 x 3 x 3 = 3³
Therefore, the prime factorization of 27 is 3³.
2. Prime Factorization of 72:
72 can be factorized as:
72 = 2 x 36 = 2 x 2 x 18 = 2 x 2 x 2 x 9 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
Therefore, the prime factorization of 72 is 2³ x 3².
3. Identifying Common Factors:
Now, compare the prime factorizations of 27 and 72:
27 = 3³ 72 = 2³ x 3²
The common prime factor is 3. The lowest power of 3 present in both factorizations is 3². Therefore, we use the lowest power in the calculation.
4. Calculating the GCF:
The GCF is the product of the common prime factors raised to their lowest power. In this case:
GCF(27, 72) = 3² = 9
Therefore, the greatest common factor of 27 and 72 is 9.
Method 2: Listing Factors
This method involves listing all the factors of each number and identifying the largest factor common to both. While less efficient for larger numbers, it's a helpful approach for building understanding.
1. Factors of 27:
The factors of 27 are 1, 3, 9, and 27.
2. Factors of 72:
The factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72.
3. Common Factors:
Comparing the lists, the common factors of 27 and 72 are 1, 3, and 9.
4. Greatest Common Factor:
The largest common factor is 9. Therefore, the GCF(27, 72) = 9.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially useful for larger numbers where prime factorization can become cumbersome. This algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Steps:
-
Divide the larger number by the smaller number and find the remainder.
72 ÷ 27 = 2 with a remainder of 18.
-
Replace the larger number with the smaller number and the smaller number with the remainder.
Now we find the GCF of 27 and 18.
-
Repeat the process.
27 ÷ 18 = 1 with a remainder of 9.
-
Continue until the remainder is 0.
18 ÷ 9 = 2 with a remainder of 0.
-
The last non-zero remainder is the GCF.
The last non-zero remainder is 9. Therefore, the GCF(27, 72) = 9.
Understanding the Mathematical Principles Behind GCF
The GCF is deeply connected to the concept of divisibility. When a number a divides another number b without leaving a remainder, we say that a is a divisor of b, or b is a multiple of a. The GCF represents the largest divisor that is common to both numbers. The prime factorization method highlights this by explicitly showing the common prime divisors and their lowest powers. The Euclidean algorithm, while seemingly different, implicitly uses this principle through repeated subtraction (or division with remainder) to arrive at the GCF.
Applications of GCF
The concept of the GCF has numerous applications across various mathematical fields and beyond:
-
Simplifying Fractions: Finding the GCF of the numerator and denominator allows for simplifying fractions to their lowest terms. For example, the fraction 27/72 can be simplified to 3/8 by dividing both the numerator and denominator by their GCF, which is 9.
-
Solving Diophantine Equations: These are equations where solutions are restricted to integers. The GCF plays a crucial role in determining the solvability and finding solutions to certain types of Diophantine equations.
-
Modular Arithmetic: In modular arithmetic, which deals with remainders after division, the GCF is essential in determining inverses and solving congruences.
-
Cryptography: GCF is utilized in various cryptographic algorithms, especially those related to public-key cryptography.
-
Computer Science: GCF algorithms are used in computer science for tasks such as finding the least common multiple (LCM) and simplifying data structures.
Frequently Asked Questions (FAQ)
Q1: What is the difference between GCF and LCM?
The greatest common factor (GCF) is the largest number that divides evenly into two or more numbers. The least common multiple (LCM) is the smallest number that is a multiple of two or more numbers. They are related; the product of the GCF and LCM of two numbers is equal to the product of the two numbers.
Q2: Can the GCF of two numbers be one?
Yes, if two numbers are relatively prime (meaning they share no common factors other than 1), their GCF is 1.
Q3: What if I have more than two numbers? How do I find their GCF?
You can extend any of the methods discussed (prime factorization, listing factors, or the Euclidean algorithm) to find the GCF of more than two numbers. For prime factorization, you'd compare the prime factorizations of all the numbers and take the common factors raised to their lowest powers. For the Euclidean algorithm, you'd find the GCF of two numbers, then find the GCF of the result and the next number, and so on.
Q4: Are there any online tools or calculators to find the GCF?
Yes, many online calculators are available that can quickly compute the GCF of two or more numbers.
Conclusion
Finding the greatest common factor (GCF) of 27 and 72, as demonstrated through various methods, provides a clear understanding of this fundamental concept in number theory. Whether using prime factorization, listing factors, or the efficient Euclidean algorithm, the result remains consistent: the GCF of 27 and 72 is 9. This exploration extends beyond a simple calculation, illuminating the underlying mathematical principles and showcasing the wide-ranging applications of the GCF in various fields of mathematics and beyond. Mastering this concept solidifies a strong foundation for more advanced mathematical studies. Understanding the GCF is not merely about finding a numerical answer; it’s about grasping the fundamental relationships between numbers and their divisors, a skill applicable far beyond the classroom.
Latest Posts
Latest Posts
-
Multiples Of 6 To 100
Sep 24, 2025
-
Is 77 Prime Or Composite
Sep 24, 2025
-
Examples Of Conservation Of Matter
Sep 24, 2025
-
Oxidation State Of Nh3 Ai
Sep 24, 2025
-
Watts To Volts Conversion Calculator
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 27 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.