Gcf Of 27 And 63
seoindie
Sep 19, 2025 · 6 min read
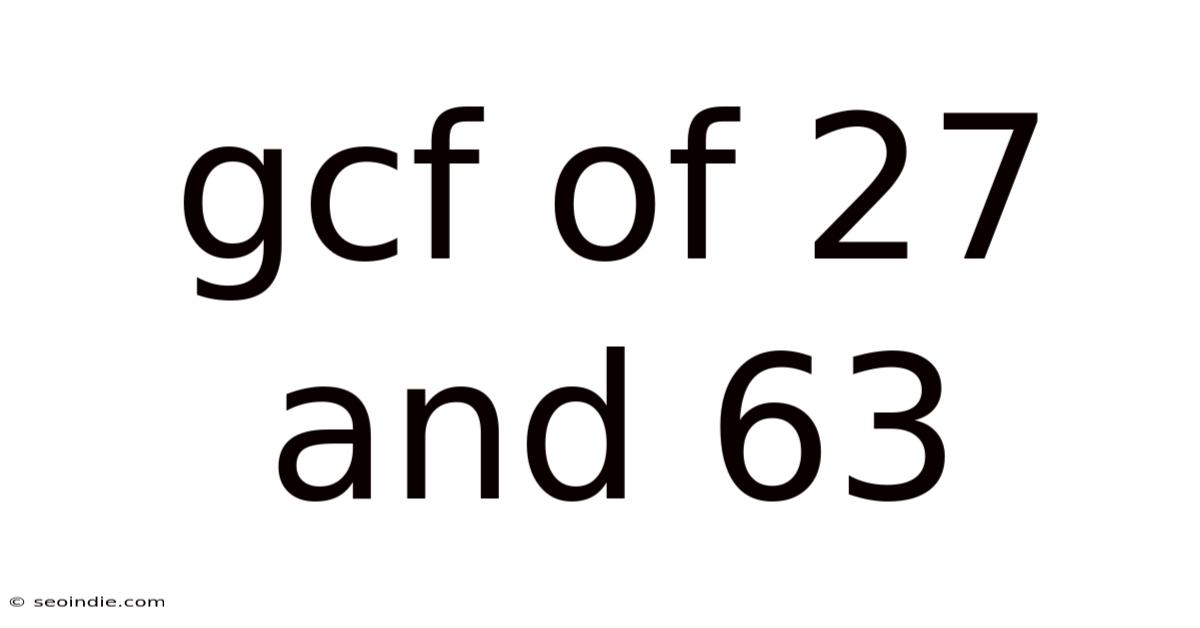
Table of Contents
Finding the Greatest Common Factor (GCF) of 27 and 63: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This guide will explore various methods to determine the GCF of 27 and 63, providing a deep understanding of the underlying principles and applications. We'll move beyond simply finding the answer and delve into the why behind the methods, ensuring you grasp the concept fully. This will be particularly helpful for students learning about prime factorization, divisibility rules, and the Euclidean algorithm.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the GCF of 12 and 18 is 6, because 6 is the largest number that divides both 12 and 18 without leaving a remainder. Understanding the GCF is crucial for simplifying fractions, solving algebraic equations, and numerous other mathematical operations.
Method 1: Prime Factorization
Prime factorization is a powerful method for finding the GCF of any two numbers. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
Steps:
-
Find the prime factorization of 27: 27 can be factored as 3 x 9, and 9 can be further factored as 3 x 3. Therefore, the prime factorization of 27 is 3 x 3 x 3, or 3³.
-
Find the prime factorization of 63: 63 can be factored as 7 x 9, and 9 can be further factored as 3 x 3. Therefore, the prime factorization of 63 is 3 x 3 x 7, or 3² x 7.
-
Identify common prime factors: Both 27 and 63 share two factors of 3.
-
Calculate the GCF: Multiply the common prime factors together. In this case, the common prime factor is 3, appearing twice in both factorizations (though 27 has an additional factor of 3). Therefore, the GCF of 27 and 63 is 3 x 3 = 9.
Therefore, the GCF of 27 and 63 is 9.
This method clearly demonstrates why 9 is the GCF. It's the product of all the prime factors common to both numbers. This approach is particularly useful for understanding the fundamental structure of numbers and their relationships.
Method 2: Listing Factors
This method is simpler for smaller numbers but can become cumbersome for larger ones.
Steps:
-
List the factors of 27: The factors of 27 are 1, 3, 9, and 27.
-
List the factors of 63: The factors of 63 are 1, 3, 7, 9, 21, and 63.
-
Identify common factors: The common factors of 27 and 63 are 1, 3, and 9.
-
Determine the greatest common factor: The largest of the common factors is 9.
Therefore, the GCF of 27 and 63 is 9.
This method is intuitive and easy to understand, especially for beginners. However, it becomes less efficient when dealing with larger numbers where listing all factors might be time-consuming and prone to errors.
Method 3: The Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Steps:
-
Divide the larger number (63) by the smaller number (27): 63 ÷ 27 = 2 with a remainder of 9.
-
Replace the larger number with the remainder: Now we find the GCF of 27 and 9.
-
Repeat the process: 27 ÷ 9 = 3 with a remainder of 0.
-
The GCF is the last non-zero remainder: Since the remainder is 0, the GCF is the previous remainder, which is 9.
Therefore, the GCF of 27 and 63 is 9.
The Euclidean algorithm is significantly more efficient than listing factors for larger numbers. Its elegance lies in its iterative nature, reducing the problem to smaller and smaller instances until the solution is reached. This method is often preferred in computer programming for its efficiency.
Understanding the Significance of the GCF
The GCF has several practical applications in mathematics and beyond:
-
Simplifying Fractions: The GCF helps simplify fractions to their lowest terms. For example, the fraction 27/63 can be simplified by dividing both the numerator and the denominator by their GCF, which is 9. This results in the simplified fraction 3/7.
-
Solving Equations: The GCF plays a role in solving certain types of algebraic equations, particularly those involving factoring.
-
Geometry: The GCF is used in geometric problems involving finding the dimensions of shapes that can be tiled with smaller squares or rectangles.
-
Number Theory: The GCF is a fundamental concept in number theory, with applications in cryptography and other advanced mathematical fields.
-
Real-World Applications: Beyond pure mathematics, the GCF finds practical applications in various fields. For example, it can help determine the largest possible size of identical squares that can be cut from a rectangular sheet of material without any waste.
Frequently Asked Questions (FAQ)
-
What if the GCF of two numbers is 1? If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they share no common factors other than 1.
-
Can the GCF of two numbers be larger than the smaller number? No. The GCF of two numbers is always less than or equal to the smaller of the two numbers.
-
Which method is best for finding the GCF? The prime factorization method provides excellent insight into the structure of the numbers. The Euclidean algorithm is the most efficient method, particularly for larger numbers. The listing factors method is suitable for smaller numbers and introductory learning.
-
Can I use the GCF to find the Least Common Multiple (LCM)? Yes. There's a relationship between the GCF and LCM of two numbers (a and b): LCM(a, b) = (a x b) / GCF(a, b). In the case of 27 and 63, the LCM is (27 x 63) / 9 = 189.
Conclusion
Finding the greatest common factor of 27 and 63, which is 9, can be achieved through various methods. Each method offers a different perspective and level of efficiency. Understanding the underlying principles of prime factorization and the Euclidean algorithm provides a strong foundation for tackling more complex mathematical problems involving GCF and LCM. The concept of GCF extends beyond simple calculations, playing a significant role in various mathematical disciplines and real-world applications. By mastering these methods, you'll gain a deeper appreciation of the interconnectedness of mathematical concepts and their practical relevance. The choice of method depends on the context and your comfort level with different techniques, but the understanding of the why behind the calculation is paramount to true mathematical literacy.
Latest Posts
Latest Posts
-
Four Letter Words In Spanish
Sep 19, 2025
-
What Does Ph Mean Text
Sep 19, 2025
-
List Vs Arraylist In Java
Sep 19, 2025
-
Lewis Structure Of Ethyl Acetate
Sep 19, 2025
-
Total Revenue Definition In Economics
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 27 And 63 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.