Gcf Of 25 And 45
seoindie
Sep 24, 2025 · 6 min read
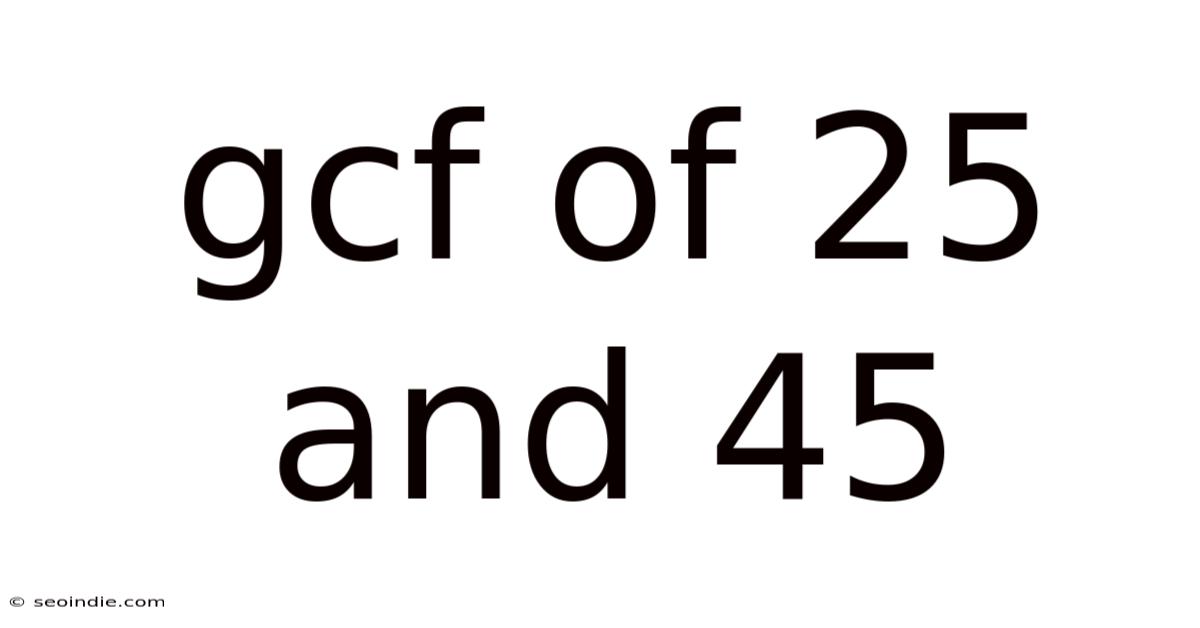
Table of Contents
Finding the Greatest Common Factor (GCF) of 25 and 45: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will explore various methods for determining the GCF of 25 and 45, providing a detailed explanation suitable for learners of all levels. We'll go beyond simply finding the answer and delve into the underlying principles, ensuring a complete understanding of this crucial mathematical concept. This guide will cover multiple approaches, from listing factors to using the Euclidean algorithm, making it a valuable resource for anyone looking to master GCF calculations.
Understanding the Greatest Common Factor (GCF)
Before we dive into calculating the GCF of 25 and 45, let's define the term. The greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all of the numbers. In simpler terms, it's the biggest number that's a factor of all the given numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The GCF of 12 and 18 is 6, because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
This concept is crucial in various mathematical applications, including simplifying fractions, solving algebraic equations, and understanding number theory. Mastering GCF calculations is an essential building block for more advanced mathematical concepts.
Method 1: Listing Factors
The most straightforward method for finding the GCF of relatively small numbers like 25 and 45 is by listing their factors.
Factors of 25: 1, 5, 25
Factors of 45: 1, 3, 5, 9, 15, 45
By comparing the lists, we can identify the common factors: 1 and 5. The greatest of these common factors is 5. Therefore, the GCF of 25 and 45 is 5.
This method is simple and easily understood, but it becomes less efficient when dealing with larger numbers. Listing all factors of large numbers can be time-consuming and prone to errors.
Method 2: Prime Factorization
Prime factorization involves expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This method is more efficient than listing factors, especially when dealing with larger numbers.
Prime Factorization of 25:
25 = 5 x 5 = 5²
Prime Factorization of 45:
45 = 3 x 3 x 5 = 3² x 5
Now, we identify the common prime factors and their lowest powers. Both 25 and 45 share a single factor of 5 (with the lowest power being 5¹). Therefore, the GCF of 25 and 45 is 5.
This method is more systematic and less prone to errors than simply listing factors. It provides a clearer understanding of the underlying structure of the numbers involved.
Method 3: The Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers where listing factors or prime factorization becomes cumbersome. This algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 25 and 45:
- Start with the larger number (45) and the smaller number (25).
- Subtract the smaller number from the larger number: 45 - 25 = 20
- Replace the larger number with the result (20), keeping the smaller number (25). Note that we now have 20 and 25. Since 25 is still larger, we continue.
- Subtract the smaller number from the larger number: 25 - 20 = 5
- Replace the larger number with the result (5), keeping the smaller number (20). Now we have 5 and 20.
- Subtract the smaller number from the larger number: 20 - 5 = 15
- Repeat the process until the two numbers are equal:
- 15 - 5 = 10
- 10 - 5 = 5
- 5 - 5 = 0
When the difference becomes 0, the last non-zero remainder is the GCF. In this case, the GCF is 5.
A more efficient way to implement the Euclidean Algorithm is through repeated division. We divide the larger number by the smaller number and find the remainder. We then replace the larger number with the smaller number and the smaller number with the remainder. We repeat this process until the remainder is 0. The last non-zero divisor is the GCF.
- Divide 45 by 25: 45 ÷ 25 = 1 with a remainder of 20.
- Divide 25 by 20: 25 ÷ 20 = 1 with a remainder of 5.
- Divide 20 by 5: 20 ÷ 5 = 4 with a remainder of 0.
The last non-zero divisor is 5, therefore the GCF of 25 and 45 is 5.
Understanding the Importance of GCF
The GCF has practical applications in various areas, including:
-
Simplifying Fractions: To simplify a fraction, we divide both the numerator and the denominator by their GCF. For example, to simplify the fraction 25/45, we divide both the numerator and denominator by their GCF, which is 5. This simplifies the fraction to 5/9.
-
Solving Algebraic Equations: The GCF plays a role in factoring algebraic expressions, which is essential for solving many algebraic equations.
-
Geometry and Measurement: GCF is used in determining the dimensions of the largest square tile that can evenly cover a rectangular area.
-
Number Theory: GCF is a fundamental concept in number theory, which studies the properties of integers.
Frequently Asked Questions (FAQ)
Q: What if I want to find the GCF of more than two numbers?
A: You can extend any of the methods described above to find the GCF of multiple numbers. For prime factorization, you find the prime factorization of each number and then identify the common prime factors with the lowest powers. For the Euclidean algorithm, you can find the GCF of two numbers, then find the GCF of that result and the next number, and so on.
Q: Are there any other methods for finding the GCF?
A: Yes, there are more advanced methods, particularly useful for very large numbers, involving concepts from abstract algebra. However, the methods discussed here are sufficient for most practical applications.
Q: Why is the Euclidean algorithm so efficient?
A: The Euclidean algorithm is efficient because it reduces the size of the numbers involved in each step, converging quickly to the GCF. It avoids the need to completely factorize the numbers, which can be computationally expensive for large numbers.
Conclusion
Finding the greatest common factor (GCF) of 25 and 45, which is 5, can be achieved using several methods. The method of listing factors is suitable for smaller numbers, while prime factorization offers a more systematic approach. The Euclidean algorithm provides the most efficient method, particularly for larger numbers. Understanding these methods and their applications is crucial for a solid foundation in mathematics and various related fields. This comprehensive guide has explored these methods in detail, equipping you with the knowledge to confidently tackle GCF problems of any complexity. Remember that choosing the right method depends on the numbers involved and your comfort level with different mathematical techniques.
Latest Posts
Latest Posts
-
Convert 2 5 To A Percent
Sep 24, 2025
-
Cremaster Muscle And Dartos Muscle
Sep 24, 2025
-
What Is Dimension Of Force
Sep 24, 2025
-
Words That Start With Gar
Sep 24, 2025
-
Is A Trapezoid A Kite
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 25 And 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.