Gcf Of 21 And 49
seoindie
Sep 18, 2025 · 6 min read
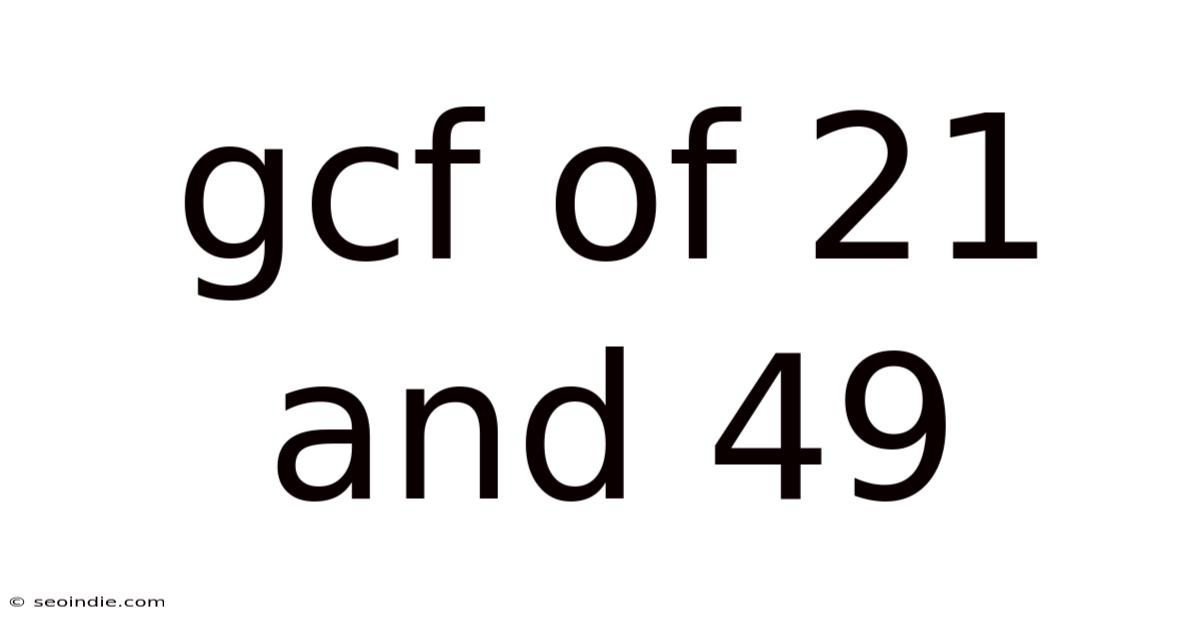
Table of Contents
Unlocking the Greatest Common Factor: A Deep Dive into GCF(21, 49)
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a deeper appreciation of number theory and its applications in various fields. This article will delve into finding the GCF of 21 and 49, exploring multiple methods, explaining the underlying mathematical principles, and expanding on the broader significance of GCF calculations. We'll move beyond simply finding the answer and illuminate the 'why' behind the process, making this concept accessible and engaging for all.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. In simpler terms, it's the biggest number that's a factor of both numbers. Understanding GCF is fundamental to simplifying fractions, solving algebraic equations, and even tackling more advanced mathematical concepts.
Let's consider our specific problem: finding the GCF of 21 and 49. This might seem straightforward, but exploring different approaches will reveal a wealth of mathematical understanding.
Method 1: Listing Factors
The most basic method for finding the GCF is listing all the factors of each number and identifying the largest common factor.
Factors of 21: 1, 3, 7, 21 Factors of 49: 1, 7, 49
Comparing the lists, we can see that the common factors are 1 and 7. The largest of these is 7. Therefore, the GCF(21, 49) = 7.
This method works well for smaller numbers, but it becomes increasingly cumbersome as the numbers grow larger. Imagine trying this method with numbers like 147 and 343! We need more efficient approaches.
Method 2: Prime Factorization
Prime factorization involves breaking down a number into its prime factors – numbers divisible only by 1 and themselves. This method provides a more systematic and efficient way to find the GCF, especially with larger numbers.
Let's find the prime factorization of 21 and 49:
- 21: 21 can be factored as 3 x 7. Both 3 and 7 are prime numbers.
- 49: 49 can be factored as 7 x 7. 7 is a prime number.
Now, we identify the common prime factors. Both 21 and 49 share a single prime factor: 7. To find the GCF, we multiply these common prime factors together. In this case, the GCF is simply 7.
This prime factorization method is significantly more efficient than listing factors, particularly when dealing with larger numbers. It provides a structured approach, making it easier to identify common factors.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers where prime factorization might become lengthy. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to find the GCF(21, 49):
- Start with the larger number (49) and the smaller number (21).
- Subtract the smaller number from the larger number: 49 - 21 = 28. Now we have the pair (21, 28).
- Repeat the process: 28 - 21 = 7. Now we have the pair (21, 7).
- Continue: 21 - 7 = 14. Now we have the pair (7, 14).
- Repeat: 14 - 7 = 7. Now we have the pair (7, 7).
- The numbers are equal! The GCF(21, 49) = 7.
The Euclidean algorithm is elegant in its simplicity and efficiency. It avoids the need for prime factorization and works effectively even with very large numbers. It's a powerful tool in number theory and has significant applications in computer science and cryptography.
Mathematical Significance of GCF
The GCF is far more than just a simple calculation. It has significant implications across various branches of mathematics:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and denominator by their GCF. For example, the fraction 21/49 can be simplified to 3/7 by dividing both the numerator and denominator by their GCF, which is 7.
-
Solving Equations: GCF plays a role in solving Diophantine equations (equations where solutions are restricted to integers). Understanding GCF helps determine the existence and nature of solutions.
-
Number Theory: GCF is a cornerstone of number theory, a branch of mathematics focused on the properties of integers. Concepts like coprime numbers (numbers with a GCF of 1) and modular arithmetic rely heavily on GCF calculations.
-
Cryptography: The Euclidean algorithm, used to find the GCF, is essential in modern cryptography, particularly in RSA encryption, a widely used public-key cryptosystem.
-
Computer Science: Efficient algorithms for finding the GCF, such as the Euclidean algorithm, are vital in computer science for various applications including optimization problems and data structure manipulation.
Beyond the Numbers: Applications in Real Life
While the application of GCF might seem confined to the mathematical realm, its principles have practical real-world applications:
-
Dividing Resources: Imagine you have 21 apples and 49 oranges to distribute equally among several baskets. Finding the GCF (7) tells you that you can make at most 7 baskets, each containing 3 apples and 7 oranges.
-
Tiling and Design: In designing tiled floors or patterns, knowing the GCF helps determine the optimal size of tiles to avoid uneven cuts and create visually appealing layouts.
-
Project Management: When managing tasks with different durations, understanding common factors can optimize scheduling and resource allocation.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
Q: Is there a formula to directly calculate the GCF?
A: While there isn't a single formula to directly compute the GCF for all numbers, the Euclidean algorithm provides a highly efficient procedural method. Prime factorization provides another method, but it doesn't translate directly into a single formula.
Q: What's the difference between GCF and LCM?
A: The GCF (Greatest Common Factor) is the largest number that divides both numbers without leaving a remainder. The LCM (Least Common Multiple) is the smallest number that is a multiple of both numbers. They are related; for any two numbers 'a' and 'b', GCF(a, b) * LCM(a, b) = a * b.
Q: Can I use a calculator to find the GCF?
A: Many scientific calculators and online calculators have built-in functions or programs to compute the GCF of two or more numbers.
Conclusion: Mastering GCF – A Stepping Stone to Mathematical Proficiency
Finding the GCF of 21 and 49, while seemingly a trivial task, serves as a gateway to understanding fundamental concepts in number theory and their far-reaching applications. Mastering different methods, like listing factors, prime factorization, and the Euclidean algorithm, enhances your mathematical toolkit and fosters a deeper appreciation for the elegance and interconnectedness of mathematical principles. Understanding GCF isn't just about solving problems; it's about cultivating a stronger foundation for more advanced mathematical explorations and appreciating the practical relevance of these concepts in various aspects of life. The seemingly simple act of finding the GCF of 21 and 49 opens doors to a wider understanding of numbers and their behavior, making it a crucial stepping stone in your mathematical journey.
Latest Posts
Latest Posts
-
Is Ssa A Congruence Theorem
Sep 18, 2025
-
2700 Sq Ft To M2
Sep 18, 2025
-
How Many Milligrams In Liter
Sep 18, 2025
-
Venn Diagram Meiosis And Mitosis
Sep 18, 2025
-
Til Vs Till Vs Until
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 21 And 49 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.