Gcf Of 15 And 18
seoindie
Sep 19, 2025 · 6 min read
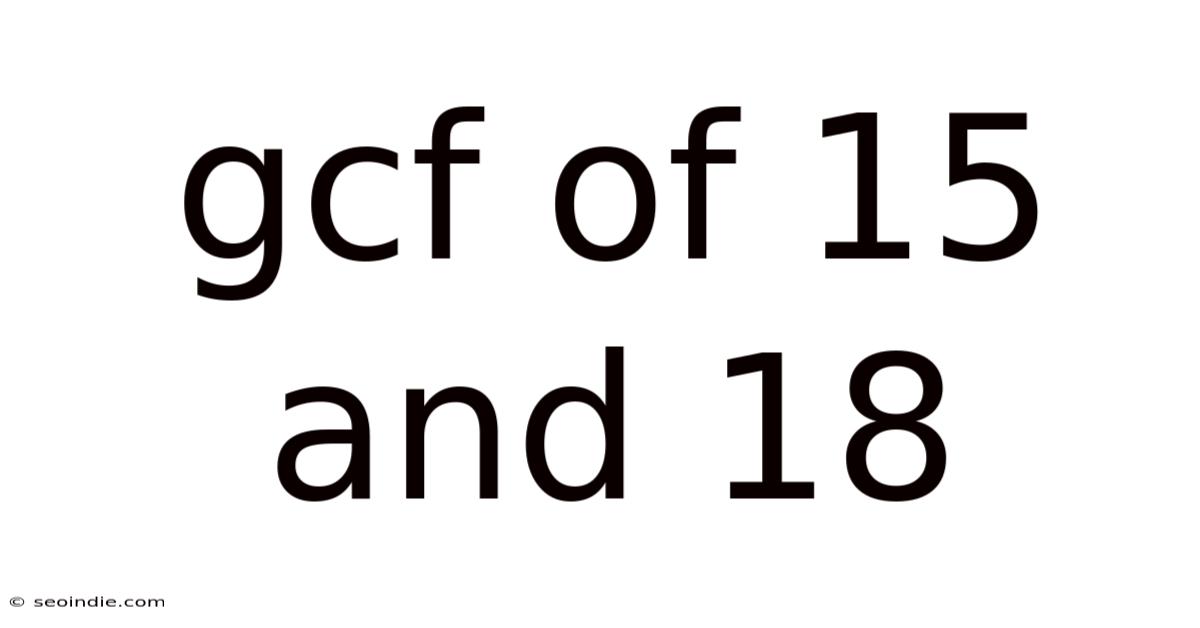
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 15 and 18: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles behind calculating the GCF opens doors to a fascinating world of number theory, with applications extending far beyond basic mathematics. This comprehensive guide will explore multiple methods for determining the GCF of 15 and 18, explain the theoretical underpinnings, and delve into related concepts to provide a thorough understanding.
Introduction: What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 perfectly. This seemingly simple concept forms the basis for many advanced mathematical operations and has significant practical applications in various fields. Understanding the GCF of 15 and 18 will serve as a stepping stone to grasping more complex number theory concepts.
Method 1: Prime Factorization
The prime factorization method is a robust and widely used technique for determining the GCF of any two numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
-
Prime Factorization of 15: 15 can be expressed as 3 x 5. Both 3 and 5 are prime numbers.
-
Prime Factorization of 18: 18 can be expressed as 2 x 3 x 3, or 2 x 3².
Once we have the prime factorization of both numbers, we identify the common prime factors and their lowest powers. In this case, the only common prime factor is 3. The lowest power of 3 present in both factorizations is 3¹ (or simply 3).
Therefore, the GCF of 15 and 18 is 3.
Method 2: Listing Factors
This method is straightforward, particularly useful for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
-
Factors of 15: 1, 3, 5, 15
-
Factors of 18: 1, 2, 3, 6, 9, 18
Comparing the two lists, we see that the common factors are 1 and 3. The greatest of these common factors is 3.
Therefore, the GCF of 15 and 18 is 3.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 15 and 18:
-
Step 1: Subtract the smaller number (15) from the larger number (18): 18 - 15 = 3
-
Step 2: Now we find the GCF of 15 and 3. Since 3 divides 15 evenly (15 ÷ 3 = 5), the GCF is 3.
Therefore, the GCF of 15 and 18 is 3.
Method 4: Using the Division Algorithm (Repeated Division)
This method is a variation of the Euclidean algorithm. Instead of subtraction, we use division with remainder.
-
Step 1: Divide the larger number (18) by the smaller number (15): 18 ÷ 15 = 1 with a remainder of 3.
-
Step 2: Now, we divide the previous divisor (15) by the remainder (3): 15 ÷ 3 = 5 with a remainder of 0.
When the remainder becomes 0, the last non-zero remainder is the GCF. In this case, the GCF is 3.
Therefore, the GCF of 15 and 18 is 3.
A Deeper Dive into Prime Factorization and its Significance
The prime factorization method, while seemingly simple, unveils fundamental concepts in number theory. Every integer greater than 1 can be uniquely expressed as a product of prime numbers. This unique factorization is known as the Fundamental Theorem of Arithmetic, a cornerstone of number theory. It allows us to analyze the structure of numbers and understand their divisibility properties.
By understanding prime factorization, we can not only find the GCF but also the least common multiple (LCM) of two numbers. The LCM is the smallest number that is a multiple of both numbers. For 15 and 18:
- Prime factorization of 15: 3 x 5
- Prime factorization of 18: 2 x 3²
To find the LCM, we take the highest power of each prime factor present in either factorization: 2¹ x 3² x 5¹ = 90. Therefore, the LCM of 15 and 18 is 90.
The relationship between GCF and LCM is expressed by the equation: GCF(a, b) x LCM(a, b) = a x b. Let's verify this for 15 and 18:
GCF(15, 18) x LCM(15, 18) = 3 x 90 = 270 15 x 18 = 270
The equation holds true, demonstrating the inherent connection between GCF and LCM.
Applications of GCF and LCM in Real-World Scenarios
The concepts of GCF and LCM aren't confined to the realm of abstract mathematics. They have practical applications in various fields:
-
Fraction Simplification: Finding the GCF allows us to simplify fractions to their lowest terms. For instance, the fraction 18/15 can be simplified to 6/5 by dividing both the numerator and denominator by their GCF, which is 3.
-
Measurement and Division: When dividing objects or quantities into equal groups, the GCF helps determine the largest possible size of those groups. For example, if you have 15 apples and 18 oranges and want to divide them into identical bags, you can create at most 3 bags, each containing 5 apples and 6 oranges.
-
Scheduling and Planning: The LCM is useful for determining when events will occur simultaneously. Imagine two events that happen every 15 days and 18 days respectively. The LCM (90) tells us that both events will coincide again after 90 days.
Frequently Asked Questions (FAQ)
-
Q: Is there only one GCF for a pair of numbers?
- A: Yes, there is only one greatest common factor for any pair of integers.
-
Q: What is the GCF of two prime numbers?
- A: The GCF of two distinct prime numbers is always 1.
-
Q: Can the GCF of two numbers be greater than the smaller number?
- A: No, the GCF can never be greater than the smaller of the two numbers.
-
Q: What if one of the numbers is 0?
- A: The GCF of any number and 0 is the absolute value of that number.
-
Q: Which method is the most efficient for finding the GCF?
- A: For larger numbers, the Euclidean algorithm or the division algorithm is generally more efficient than prime factorization or listing factors.
Conclusion: Beyond the Basics
Finding the GCF of 15 and 18, while a seemingly elementary task, serves as a gateway to a deeper understanding of number theory. The various methods presented here illustrate the interconnectedness of mathematical concepts and their practical applications. Understanding these concepts not only strengthens your arithmetic skills but also provides a foundation for tackling more advanced mathematical problems and real-world challenges involving divisibility, simplification, and scheduling. The seemingly simple act of finding the GCF illuminates the beauty and power of mathematics in its elegance and practicality.
Latest Posts
Latest Posts
-
Lcm Of 50 And 75
Sep 19, 2025
-
300m Is How Many Feet
Sep 19, 2025
-
One Hundred Million In Numbers
Sep 19, 2025
-
What Number Has 19 Zeros
Sep 19, 2025
-
Vegetables That Start With W
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 15 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.