Gcf Of 12 And 32
seoindie
Sep 14, 2025 · 7 min read
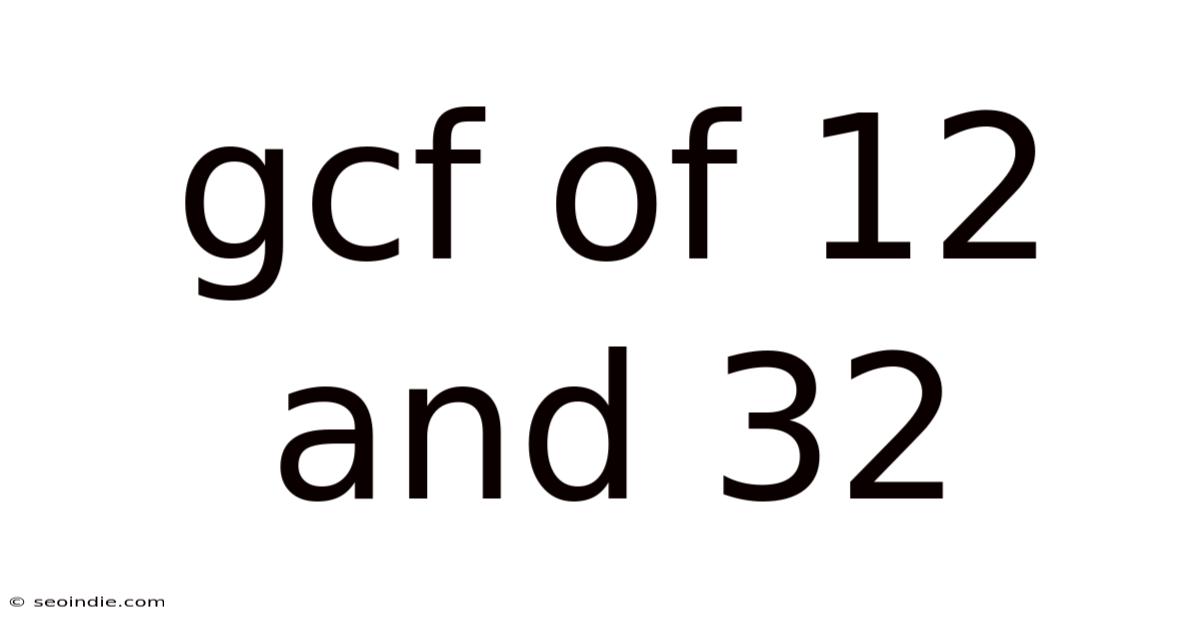
Table of Contents
Finding the Greatest Common Factor (GCF) of 12 and 32: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. Understanding GCF is crucial for simplifying fractions, solving algebraic equations, and even tackling more advanced mathematical problems. This article will provide a detailed explanation of how to find the GCF of 12 and 32, exploring various methods and delving into the underlying mathematical principles. We'll also address frequently asked questions and provide practical examples to solidify your understanding.
Understanding Greatest Common Factor (GCF)
Before we dive into calculating the GCF of 12 and 32, let's define what it means. The greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all of the given numbers without leaving a remainder. In simpler terms, it's the biggest number that is a factor of all the numbers in question.
For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 32 are 1, 2, 4, 8, 16, and 32. The common factors of 12 and 32 are 1, 2, and 4. The greatest of these common factors is 4. Therefore, the GCF of 12 and 32 is 4.
Method 1: Listing Factors
This method is straightforward and works well for smaller numbers. It involves listing all the factors of each number and then identifying the largest common factor.
Steps:
- List the factors of 12: 1, 2, 3, 4, 6, 12
- List the factors of 32: 1, 2, 4, 8, 16, 32
- Identify the common factors: 1, 2, 4
- Determine the greatest common factor: 4
Therefore, the GCF of 12 and 32 using the listing factors method is 4. This method is easy to visualize but can become cumbersome with larger numbers.
Method 2: Prime Factorization
Prime factorization is a more efficient method, particularly for larger numbers. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Steps:
- Find the prime factorization of 12: 12 = 2 x 2 x 3 = 2² x 3
- Find the prime factorization of 32: 32 = 2 x 2 x 2 x 2 x 2 = 2⁵
- Identify common prime factors: The only common prime factor is 2.
- Determine the lowest power of the common prime factors: The lowest power of 2 present in both factorizations is 2².
- Multiply the lowest powers of common prime factors: 2² = 4
Therefore, the GCF of 12 and 32 using prime factorization is 4. This method is more systematic and less prone to error, especially when dealing with larger numbers.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Steps:
- Start with the larger number (32) and the smaller number (12).
- Divide the larger number by the smaller number and find the remainder: 32 ÷ 12 = 2 with a remainder of 8.
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (8).
- Repeat step 2: 12 ÷ 8 = 1 with a remainder of 4.
- Repeat step 3: Replace 8 with 4, and the remainder becomes the new smaller number.
- Repeat step 2: 8 ÷ 4 = 2 with a remainder of 0.
- When the remainder is 0, the GCF is the last non-zero remainder. In this case, the GCF is 4.
Therefore, the Euclidean algorithm confirms that the GCF of 12 and 32 is 4. This method is particularly efficient for large numbers because it avoids the need to find all factors.
Mathematical Explanation of the GCF
The GCF is fundamentally linked to the concept of divisibility. When a number 'a' divides evenly into another number 'b', we say 'a' is a factor of 'b', and 'b' is a multiple of 'a'. The GCF represents the largest number that simultaneously acts as a factor for both (or all) the numbers in question. This concept is deeply rooted in number theory and has significant implications in various areas of mathematics, including:
- Fraction simplification: Finding the GCF allows you to simplify fractions to their lowest terms. For example, the fraction 12/32 can be simplified to 3/8 by dividing both the numerator and denominator by their GCF, which is 4.
- Algebraic expressions: GCF is used to factor algebraic expressions, which simplifies them and makes them easier to solve.
- Modular arithmetic: The concept of GCF is essential in modular arithmetic, a branch of number theory that deals with remainders after division.
- Cryptography: GCF plays a role in certain cryptographic algorithms, which are used to secure data.
Applications of GCF in Real-World Scenarios
While the concept of GCF might seem abstract, it has many practical applications in everyday life:
- Dividing objects evenly: If you have 12 apples and 32 oranges, and you want to divide them into the largest possible equal groups, the GCF (4) tells you that you can make 4 equal groups, each containing 3 apples and 8 oranges.
- Planning events: Imagine you're organizing a party and you need to arrange chairs in equal rows and columns. If you have 12 red chairs and 32 blue chairs, the GCF helps you determine the maximum number of chairs per row or column for an even arrangement.
- Construction and design: In architecture and construction, GCF principles are used for creating uniform patterns and efficient layouts.
- Computer science: In algorithms and data structures, finding the greatest common divisor is crucial for tasks like optimizing code and improving efficiency.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they share no common factors other than 1.
Q: Can the GCF of two numbers be one of the numbers itself?
A: Yes, if one number is a multiple of the other, the GCF will be the smaller number. For example, the GCF of 12 and 24 is 12.
Q: Is there a limit to the number of numbers for which we can find the GCF?
A: No, the GCF can be found for any number of integers. The methods described above can be extended to find the GCF of three or more numbers. For example, to find the GCF of 12, 32, and 48, you would first find the GCF of 12 and 32 (which is 4), and then find the GCF of 4 and 48 (which is 4). Therefore, the GCF of 12, 32, and 48 is 4.
Q: Are there any online calculators or software tools that can help find the GCF?
A: Yes, many online calculators and mathematical software packages can quickly calculate the GCF of any set of numbers. These tools can be particularly helpful when dealing with very large numbers.
Conclusion
Finding the greatest common factor is a valuable skill with broad applications across various mathematical fields and real-world scenarios. We’ve explored three primary methods—listing factors, prime factorization, and the Euclidean algorithm—each with its own strengths and weaknesses. Understanding these methods, along with the underlying mathematical principles, empowers you to confidently tackle problems involving GCF, whether it's simplifying fractions, solving equations, or tackling more advanced mathematical concepts. Remember, the choice of method often depends on the size of the numbers involved and your personal preference. Mastering the concept of GCF provides a solid foundation for further exploration in mathematics and its numerous applications.
Latest Posts
Latest Posts
-
17cm Is How Many Inches
Sep 14, 2025
-
Quarts To Cubic Feet Conversion
Sep 14, 2025
-
Ejemplos De Monocotiledoneas Y Dicotiledoneas
Sep 14, 2025
-
How Many Feet Is 78
Sep 14, 2025
-
Cubic Ft To Liter Conversion
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 12 And 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.