Factors Of 140 In Pairs
seoindie
Sep 25, 2025 · 6 min read
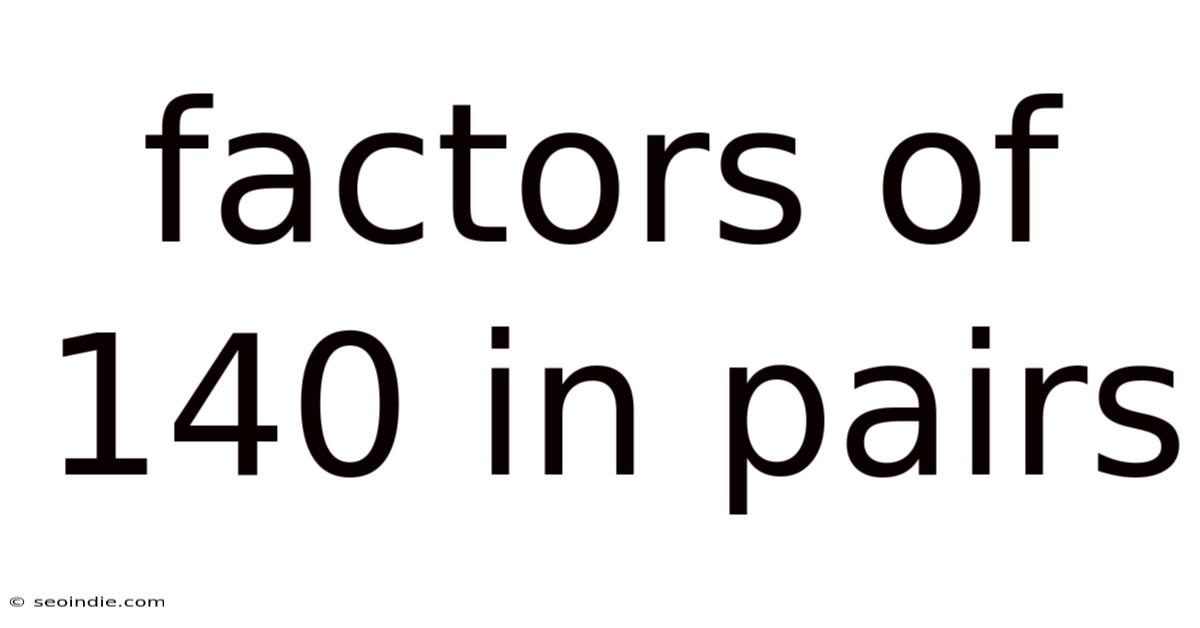
Table of Contents
Unveiling the Pairs of Factors of 140: A Deep Dive into Number Theory
Finding the factors of a number is a fundamental concept in number theory, forming the bedrock for understanding more complex mathematical ideas. This article delves into the fascinating world of factors, specifically exploring the pairs of factors for the number 140. We'll not only identify all the factor pairs but also explore the underlying mathematical principles, providing a comprehensive understanding suitable for students and enthusiasts alike. We'll also touch upon related concepts and answer frequently asked questions. Understanding factors is key to grasping concepts like prime factorization, greatest common divisors, and least common multiples.
Understanding Factors and Factor Pairs
Before we embark on our journey to find the factor pairs of 140, let's define what we mean by factors and factor pairs. A factor of a number is a whole number that divides the number evenly without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 perfectly.
A factor pair consists of two factors whose product is the original number. For instance, for the number 12, the factor pairs are (1, 12), (2, 6), and (3, 4). Notice that the order matters in defining a pair; (2, 6) is distinct from (6, 2), although both represent the same factors.
Finding the Factors of 140: A Step-by-Step Approach
There are several methods to find the factors of 140. Let's explore a systematic approach that ensures we don't miss any:
1. Prime Factorization: The first step is to find the prime factorization of 140. Prime factorization involves expressing a number as a product of its prime factors. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
140 can be broken down as follows:
140 = 10 x 14 = (2 x 5) x (2 x 7) = 2² x 5 x 7
This tells us that the prime factors of 140 are 2, 5, and 7. The exponents (2, 1, and 1) indicate that 2 appears twice, while 5 and 7 appear once each.
2. Systematic Listing: Now that we have the prime factorization, we can systematically list all the factors. We do this by considering all possible combinations of the prime factors and their powers:
- Using only 2: 2, 4 (2²)
- Using 5: 5, 10 (2 x 5), 20 (2² x 5), 70 (2 x 5 x 7), 140 (2² x 5 x 7)
- Using 7: 7, 14 (2 x 7), 35 (5 x 7), 70 (2 x 5 x 7), 140 (2² x 5 x 7)
- Using 1: 1
This process accounts for all possible combinations and ensures that no factor is missed. We've identified the factors as 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, and 140.
3. Identifying Factor Pairs: Finally, we pair these factors to obtain all the factor pairs of 140:
- (1, 140)
- (2, 70)
- (4, 35)
- (5, 28)
- (7, 20)
- (10, 14)
These six pairs represent all the possible combinations of two factors whose product equals 140. Note that we have listed each pair only once, respecting the order.
Mathematical Significance of Factors and Factor Pairs
The concept of factors and factor pairs extends far beyond simply listing numbers. They form the basis for understanding various mathematical concepts:
-
Greatest Common Divisor (GCD): The GCD of two numbers is the largest number that divides both numbers evenly. Knowing the factors of each number helps determine their GCD. For example, to find the GCD of 140 and another number, we would compare their factor lists.
-
Least Common Multiple (LCM): The LCM of two numbers is the smallest number that is a multiple of both numbers. Again, understanding the prime factorization and factors is crucial for calculating the LCM efficiently.
-
Divisibility Rules: Factors are closely linked to divisibility rules. For example, because 2 is a factor of 140, 140 is divisible by 2. Understanding factors makes divisibility rules more intuitive.
-
Algebraic Equations: Factorization is a crucial technique in solving algebraic equations. Expressing an algebraic expression as a product of its factors simplifies the equation and often leads to solutions.
-
Cryptography: Factorization plays a critical role in modern cryptography, specifically in systems based on prime numbers and their properties. The difficulty of factoring large numbers into their prime components is the foundation of many encryption algorithms.
Further Exploration: Beyond the Basics
The exploration of factors doesn't end with finding the pairs for 140. Consider these extensions:
-
Number of Factors: A formula exists to determine the number of factors a number has, based on its prime factorization. For 140 (2² x 5¹ x 7¹), the number of factors is (2+1)(1+1)(1+1) = 12.
-
Perfect Numbers: A perfect number is a positive integer that is equal to the sum of its proper divisors (divisors excluding the number itself). Exploring perfect numbers deepens understanding of factors and their relationships.
-
Abundant and Deficient Numbers: These classifications extend the concept of perfect numbers. An abundant number has a sum of its proper divisors greater than the number itself, while a deficient number has a sum of its proper divisors less than the number itself.
-
Highly Composite Numbers: These are numbers that have more divisors than any smaller positive integer. Investigating these numbers requires a deep understanding of factor counts and their distribution.
Frequently Asked Questions (FAQ)
Q: Is there a quicker method to find factor pairs besides systematic listing?
A: While systematic listing is reliable, for smaller numbers, you can use mental math and trial division. Start with 1 and check for pairs systematically until you reach the square root of the number. After that point, you will simply be repeating the pairs you've already found (in reverse order).
Q: Why is prime factorization important in finding factors?
A: Prime factorization provides a fundamental building block. Once you have the prime factors, you can generate all other factors by combining them in various ways. This ensures you capture all factors without missing any.
Q: Can a number have an odd number of factors?
A: Yes, but only if the number is a perfect square. Perfect squares have an odd number of factors because the square root of the number pairs with itself.
Q: What is the significance of the square root in finding factors?
A: When searching for factors, you only need to check up to the square root of the number. Any factor beyond the square root will have a corresponding factor smaller than the square root. This significantly reduces the number of trial divisions required.
Conclusion: A Comprehensive Understanding of Factors
This article has provided a comprehensive exploration of the factors of 140, detailing the methods for finding its factor pairs and delving into the broader mathematical significance of this fundamental concept. Understanding factors is a cornerstone of number theory, paving the way for understanding more advanced mathematical ideas and applications in various fields. We hope this detailed guide has not only helped you identify the factor pairs of 140 but has also deepened your understanding of the underlying principles and applications of this critical mathematical concept. Remember, the beauty of mathematics lies in its interconnectedness – a deep understanding of seemingly simple concepts like factors unlocks a world of possibilities.
Latest Posts
Latest Posts
-
What Is The Causative Agent
Sep 25, 2025
-
Bases Make Litmus Paper Turn
Sep 25, 2025
-
2 To Power Of 16
Sep 25, 2025
-
Multiplication Of 1 To 100
Sep 25, 2025
-
Name A Way Of Transportation
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Factors Of 140 In Pairs . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.