62 Minus What Equals 15
seoindie
Sep 20, 2025 · 5 min read
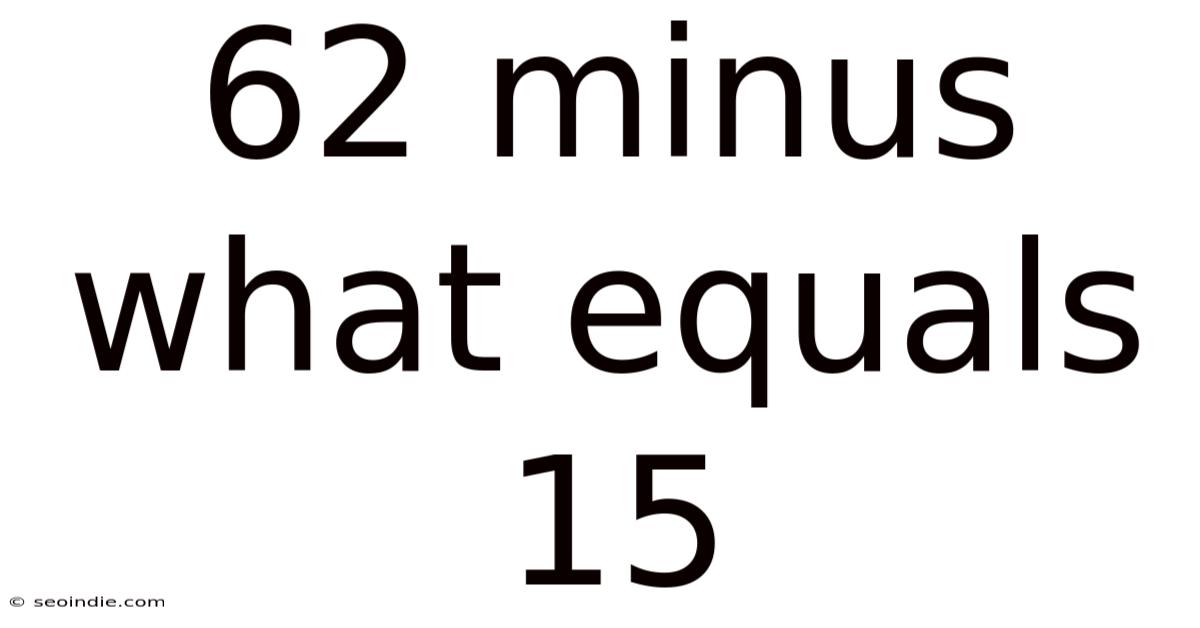
Table of Contents
62 Minus What Equals 15: Unveiling the Mystery of Subtraction and Number Relationships
This article delves into the seemingly simple question: "62 minus what equals 15?" While the answer might appear immediately obvious to some, we'll explore this problem in depth, uncovering the underlying mathematical principles, demonstrating different solution methods, and expanding our understanding of number relationships and problem-solving strategies. This exploration will be beneficial for anyone seeking to improve their mathematical skills, from elementary school students to adults looking to refresh their fundamental arithmetic knowledge. We’ll cover various approaches, including basic subtraction, algebraic manipulation, and even visual representations to solidify comprehension.
Understanding the Problem: Deconstructing Subtraction
At its core, the problem "62 minus what equals 15" is a subtraction equation. In mathematical terms, we can represent this as:
62 - x = 15
Where 'x' represents the unknown number we are trying to find. Subtraction, in its simplest form, is the process of taking away a quantity from another. Understanding this fundamental concept is crucial to solving the equation.
Method 1: Direct Subtraction and Inverse Operations
The most straightforward method to solve this is by using the inverse operation of subtraction, which is addition. To isolate 'x' and find its value, we need to manipulate the equation.
-
Isolate the variable: We want to get 'x' by itself on one side of the equation. To do this, we can add 'x' to both sides:
62 - x + x = 15 + x
This simplifies to:
62 = 15 + x
-
Solve for x: Now, we need to isolate 'x' further. We can subtract 15 from both sides of the equation:
62 - 15 = 15 + x - 15
This simplifies to:
47 = x
Therefore, x = 47. This means that 62 minus 47 equals 15.
Method 2: Visual Representation – The Number Line
A visual approach can be incredibly helpful, especially for those who prefer a more concrete understanding. We can use a number line to illustrate the problem.
Imagine a number line stretching from 0 to 62. We start at 62 and need to move back (subtract) until we reach 15. The distance we move back represents the value of 'x'. By counting backwards from 62 to 15, or by subtracting 15 from 62 directly, we arrive at the same answer: 47.
Method 3: Algebraic Manipulation – A More Formal Approach
For more complex problems, algebraic manipulation becomes essential. We've already shown this method implicitly in Method 1, but let's explicitly outline the steps:
-
Start with the equation: 62 - x = 15
-
Add 'x' to both sides: 62 = 15 + x
-
Subtract 15 from both sides: 62 - 15 = x
-
Solve for x: x = 47
This algebraic approach highlights the importance of maintaining balance in an equation. Whatever operation we perform on one side, we must perform the same operation on the other side to preserve the equality.
Expanding the Understanding: Beyond the Simple Solution
While finding the answer (47) is straightforward, let's delve into the broader mathematical concepts this problem illuminates:
-
Inverse Operations: The problem beautifully illustrates the concept of inverse operations. Subtraction and addition are inverses; they "undo" each other. This is a fundamental principle in algebra and higher-level mathematics.
-
Number Relationships: The problem highlights the relationship between the numbers 62, 15, and 47. Understanding these relationships helps develop number sense and mental arithmetic skills.
-
Problem-Solving Strategies: The problem demonstrates different strategies for solving mathematical problems: direct calculation, visual representation, and algebraic manipulation. Choosing the appropriate strategy depends on the problem's complexity and individual preferences.
-
Real-World Applications: Subtraction problems like this are applied extensively in everyday life. From calculating change after a purchase to managing finances and solving various practical problems, the ability to solve subtraction problems efficiently is crucial.
Frequently Asked Questions (FAQs)
-
Q: Can this problem be solved using different mathematical operations? A: While the problem is fundamentally a subtraction problem, we used addition (the inverse operation) to solve for x. Other methods, like using a number line or visual aids, might also be considered different approaches, but they ultimately rely on the underlying principles of subtraction.
-
Q: What if the numbers were larger? A: The same principles would apply. Regardless of the size of the numbers, you can always use the inverse operation (addition) to solve for the unknown variable. For larger numbers, a calculator might be helpful for the arithmetic, but the underlying algebraic manipulation remains the same.
-
Q: Are there other ways to represent this problem? A: Yes, the problem could be presented as a word problem. For example: "John had 62 apples. After giving some away, he had 15 left. How many apples did he give away?" This shows how the mathematical concept applies to real-world scenarios.
-
Q: What if the problem was 15 minus what equals 62? A: This would result in a negative solution. The equation would be 15 - x = 62. Solving this would yield x = -47. This introduces the concept of negative numbers and further expands our understanding of number lines and their extensions beyond zero.
Conclusion: Mastering Subtraction and Beyond
The seemingly simple question, "62 minus what equals 15?" offers a profound entry point into the world of mathematics. By exploring different solution methods and examining the underlying principles of subtraction, inverse operations, and number relationships, we've gained a deeper appreciation for fundamental mathematical concepts. The ability to solve problems like this efficiently is not only valuable for academic success but also for navigating the complexities of everyday life. Remember that mathematical proficiency is built upon a strong foundation of understanding and practice. Keep exploring, keep asking questions, and keep practicing—the rewards are limitless.
Latest Posts
Latest Posts
-
Adj That Start With G
Sep 21, 2025
-
Math Problems That Equal 13
Sep 21, 2025
-
Words Starting With M I
Sep 21, 2025
-
400 Square Meters In Feet
Sep 21, 2025
-
Division Of Complex Numbers Calculator
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 62 Minus What Equals 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.