6 X 3 X 1
seoindie
Sep 19, 2025 · 6 min read
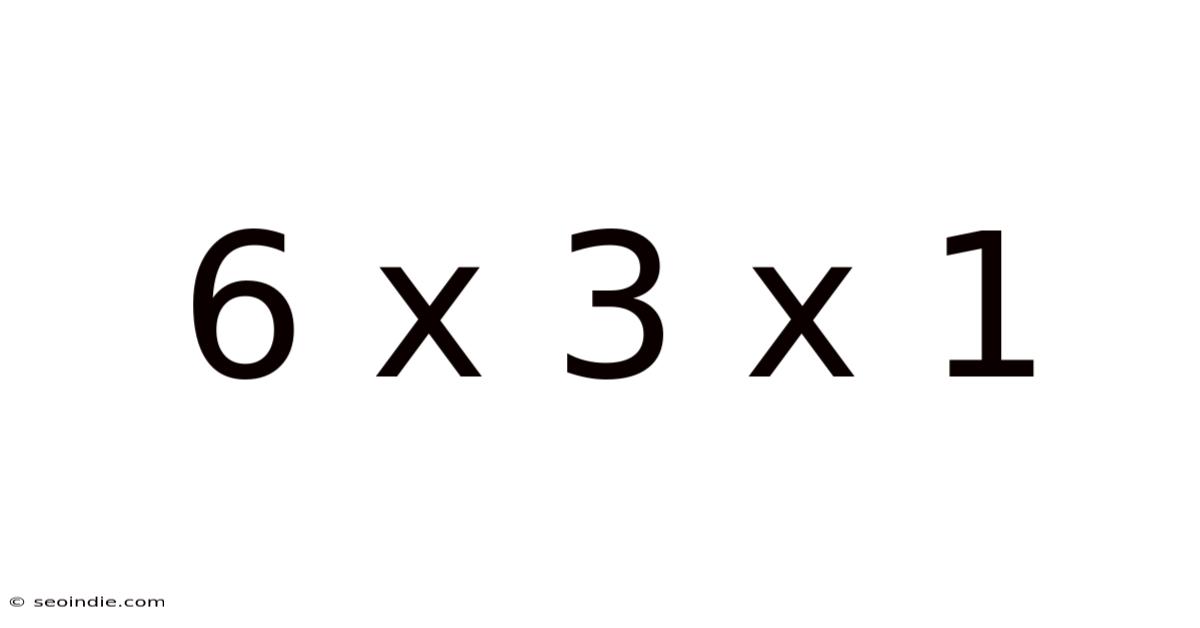
Table of Contents
Decoding 6 x 3 x 1: Exploring Dimensions, Applications, and Interpretations
The seemingly simple expression "6 x 3 x 1" can unlock a surprising depth of understanding across various fields. While at first glance it appears to be a straightforward multiplication problem equaling 18, its implications extend far beyond basic arithmetic. This article will explore the multifaceted interpretations of 6 x 3 x 1, examining its relevance in geometry, data analysis, combinatorics, and even abstract thought. We'll delve into the underlying principles, providing practical examples and illustrative scenarios to enhance your comprehension.
Introduction: Beyond the Obvious Calculation
The initial reaction to "6 x 3 x 1" is likely the calculation itself: 6 multiplied by 3, resulting in 18, then multiplied by 1, remaining at 18. However, the true significance lies in understanding the dimensions represented by these numbers. Each number can be interpreted as a dimension within a system, opening possibilities for spatial representation, data structuring, and problem-solving in diverse contexts. Understanding these dimensional interpretations is key to unlocking the deeper meanings embedded within this seemingly simple expression.
1. Geometric Interpretations: Volume and Spatial Relationships
The numbers 6, 3, and 1 can be directly visualized as dimensions in three-dimensional space. Imagine a rectangular prism (or cuboid):
- 6 units: Represents the length of the prism.
- 3 units: Represents the width of the prism.
- 1 unit: Represents the height of the prism.
The calculation 6 x 3 x 1 then becomes the formula for calculating the volume of this prism. The volume is 18 cubic units. This simple geometric interpretation immediately provides a tangible representation of the numerical expression. We can further explore variations: if the numbers represent different units (e.g., centimeters, meters), the resulting volume will be expressed in cubic centimeters or cubic meters respectively.
Beyond simple volumes, the expression can represent more complex spatial relationships. Consider a scenario involving arranging objects in a three-dimensional grid. The numbers could represent the number of units along each axis. For instance, arranging boxes in a warehouse: 6 boxes along the length, 3 boxes along the width, and only 1 layer high. The total number of boxes would be 18.
2. Data Analysis and Array Structures:
In data analysis and programming, the expression 6 x 3 x 1 can represent the dimensions of a multi-dimensional array or matrix. Imagine a dataset structured as follows:
- 6: Number of rows.
- 3: Number of columns.
- 1: Number of layers (or depth – in a 3D array).
This would represent a 6 x 3 matrix (or a 6 x 3 x 1 three-dimensional array which is essentially a flattened 3D array). Each cell within this matrix could hold a specific data point, such as measurements, observations, or any other type of information. This dimensional structure is crucial for organizing and manipulating large datasets efficiently. Understanding this allows for the efficient retrieval and processing of specific data points within the array.
The "1" dimension might seem redundant here, but in higher-dimensional arrays, it becomes significant. Consider a similar array with a 'depth' greater than one; this extra dimension allows for more complex representations. For example, this could be used to store data across multiple time points or different experimental conditions.
3. Combinatorics and Permutations:
While not a direct application of multiplication, the numbers 6, 3, and 1 can be relevant to combinatorial problems. If we consider these numbers as representing distinct choices or categories, we can analyze the number of possible combinations or permutations. For example:
- 6 options for color: (Red, Blue, Green, Yellow, Orange, Purple)
- 3 options for size: (Small, Medium, Large)
- 1 option for material: (Cotton)
The total number of unique combinations of color, size, and material would be 6 x 3 x 1 = 18. This illustrates how the expression relates to counting the total number of possibilities when multiple independent choices are available. This approach extends to more complex scenarios involving multiple categories with varying numbers of options within each.
4. Abstract Interpretations and Symbolic Representation:
Beyond the concrete applications, the expression "6 x 3 x 1" can take on symbolic meaning depending on the context. The numbers themselves might represent abstract concepts, and the multiplication operation could symbolize a relationship or interaction between those concepts. For example, in philosophy or symbolic logic, these numbers could represent different elements of a system, and the multiplication could represent their synthesis or integration. The resulting value (18) could then represent the outcome or consequence of this interaction.
The inherent ambiguity allows for diverse interpretations depending on the intended symbolic representation. The flexibility of such an expression opens it up for creative exploration in various abstract fields, offering fertile ground for theoretical development and nuanced analysis.
5. Practical Applications and Real-World Examples:
The implications of understanding "6 x 3 x 1" extend to various practical applications:
- Inventory Management: Determining the total number of items in a warehouse based on dimensions of storage space.
- Production Planning: Calculating the total number of products that can be produced given the available resources.
- Project Management: Estimating the total workload by breaking down tasks into sub-tasks and quantifying their individual efforts.
- Game Development: Designing levels in a video game, defining grid dimensions for map creation or resource allocation.
- Data Visualization: Representing data using multi-dimensional charts or graphs, enabling efficient data exploration.
Frequently Asked Questions (FAQ)
-
Q: Is the order of the numbers important in 6 x 3 x 1?
- A: In standard multiplication, the order does not matter (commutative property). However, in the context of spatial dimensions or array structures, the order represents the sequence of dimensions and is therefore crucial. A 6 x 3 x 1 array is fundamentally different from a 1 x 3 x 6 array.
-
Q: Can the "1" be omitted?
- A: Mathematically, multiplying by 1 doesn't change the result. However, in the context of dimensions, the "1" represents a significant dimension, even if it only has a single unit. Omitting it would lose the information about the dimensionality of the system.
-
Q: What if the numbers were different?
- A: The same principles apply. Any set of three numbers can represent dimensions, whether in geometry, data structures, or combinatorial problems. The interpretation and applications would change accordingly. The approach remains consistent; analyze the dimensions and their implications within the given context.
Conclusion: Unlocking the Potential of Simple Expressions
While "6 x 3 x 1" might seem like a trivial mathematical expression, its potential for understanding expands significantly when considering its various interpretations. From geometric volumes and data structures to combinatorial possibilities and abstract symbolism, this seemingly simple equation opens doors to deeper comprehension across numerous disciplines. By appreciating the dimensional aspect and considering the context in which the numbers are applied, we can unlock the wealth of insights embedded within even the most basic mathematical expressions. The true power lies not just in the calculation but in the understanding of the underlying principles and their multifaceted applications. Remember, the seemingly simple often holds hidden depths, and exploring these depths can lead to unexpected discoveries and a richer understanding of the world around us.
Latest Posts
Latest Posts
-
Calculate Standard Error In Excel
Sep 19, 2025
-
Mammals Amphibians Reptiles Fish Birds
Sep 19, 2025
-
Greatest Common Factor Of 6
Sep 19, 2025
-
What Is A Cohesive Force
Sep 19, 2025
-
Fog Poem By Carl Sandburg
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 6 X 3 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.