6 5 X 2 10
seoindie
Sep 23, 2025 · 5 min read
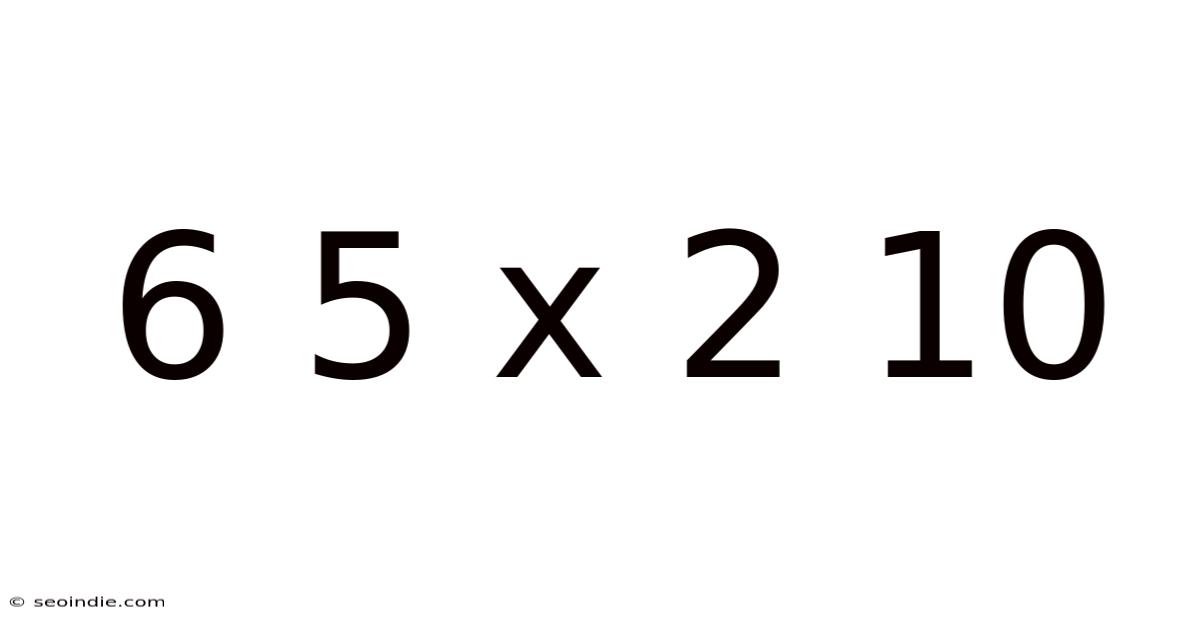
Table of Contents
Decoding 65 x 210: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem, 65 x 210, as a gateway to understanding fundamental mathematical concepts and their wide-ranging applications. We'll move beyond simply finding the answer to delve into the why behind the method, exploring different approaches, and showcasing the relevance of this seemingly basic calculation in various fields. Understanding multiplication, even at this level, forms the bedrock for more advanced mathematical concepts.
Introduction: Beyond the Numbers
At first glance, 65 x 210 appears straightforward. A simple multiplication problem solvable with a calculator in seconds. But this simplicity belies a deeper significance. This problem offers a chance to explore different multiplication techniques, enhancing our understanding of place value, distributive properties, and the very essence of multiplication itself. The result, 13650, is more than just a number; it represents a powerful concept with real-world applications across numerous disciplines, from basic accounting to complex engineering calculations.
Method 1: Standard Multiplication Algorithm
The most common method taught in schools is the standard long multiplication algorithm. This method systematically breaks down the problem, handling each place value separately. Let's work through it step-by-step:
-
Set up the problem: Write the numbers vertically, aligning the units digits.
65 x 210 ------ -
Multiply by the units digit (0): Multiplying 65 by 0 results in 0. Write this below the line.
65 x 210 ------ 0 -
Multiply by the tens digit (1): Multiply 65 by 1 (which is effectively multiplying by 10 since it's in the tens place). Write the result, 65, shifted one place to the left.
65 x 210 ------ 0 65 -
Multiply by the hundreds digit (2): Multiply 65 by 2 (which is effectively multiplying by 200 since it's in the hundreds place). Write the result, 130, shifted two places to the left.
65 x 210 ------ 0 65 130 -
Add the partial products: Add the three partial products (0, 65, and 130) to get the final answer.
65 x 210 ------ 0 65 130 ------ 13650
Therefore, 65 x 210 = 13650. This method emphasizes the concept of place value and the distributive property of multiplication.
Method 2: Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can apply this property to simplify the calculation:
We can rewrite 210 as 200 + 10. Then:
65 x 210 = 65 x (200 + 10) = (65 x 200) + (65 x 10)
- 65 x 200 = 13000
- 65 x 10 = 650
Adding the results: 13000 + 650 = 13650
This approach showcases a deeper mathematical understanding, demonstrating the underlying principles of multiplication. It's often easier to perform mental calculations using the distributive property, especially with simpler numbers.
Method 3: Factorization
We can further break down the numbers using factorization. This involves finding the prime factors of each number.
- 65 = 5 x 13
- 210 = 2 x 3 x 5 x 7
Then, 65 x 210 = (5 x 13) x (2 x 3 x 5 x 7) = 2 x 3 x 5 x 5 x 7 x 13 = 13650
This approach highlights the fundamental building blocks of numbers and their multiplicative relationships.
Real-World Applications: Where Does 65 x 210 Matter?
While seemingly simple, the principle behind 65 x 210 applies to numerous real-world situations:
- Business and Finance: Calculating total revenue from selling 65 items at $210 each.
- Inventory Management: Determining the total number of items in 65 boxes, each containing 210 items.
- Construction and Engineering: Calculating the total area of a rectangular space measuring 65 units by 210 units.
- Data Analysis: Calculating the total number of data points in a dataset with 65 groups of 210 data points each.
- Everyday Life: Calculating the total cost of 65 items priced at $210 each.
Expanding the Concept: Beyond Basic Multiplication
Understanding 65 x 210 extends beyond the simple act of multiplication. It helps us develop crucial skills including:
- Estimation: Before calculating, we can estimate the answer. 65 is roughly 70, and 210 is roughly 200, so an approximate answer would be 70 x 200 = 14000. This ability to estimate is vital for checking the reasonableness of our calculations.
- Mental Math: Practicing different multiplication methods improves mental calculation skills.
- Problem-Solving: Real-world problems often require translating word problems into mathematical equations, like the examples above.
Frequently Asked Questions (FAQ)
-
Q: What is the quickest way to calculate 65 x 210? A: Using a calculator is the fastest way. However, understanding the different methods allows for quicker mental calculations in simpler scenarios.
-
Q: Why is it important to learn different multiplication methods? A: Learning multiple methods enhances understanding, provides flexibility in problem-solving, and improves mental math abilities.
-
Q: How can I improve my multiplication skills? A: Consistent practice using different methods, focusing on understanding the underlying principles, and working through various problems of increasing complexity are all effective strategies.
-
Q: Are there any tricks to make multiplication easier? A: Yes, learning the distributive property, using factorization, and practicing mental math techniques can significantly simplify multiplication.
Conclusion: The Enduring Power of a Simple Equation
The seemingly simple equation, 65 x 210, serves as a powerful illustration of fundamental mathematical concepts and their practical applications. While finding the answer (13650) is important, the real value lies in understanding the process – the methods, the principles, and the wide-ranging applications. By exploring different approaches and appreciating the underlying mathematical principles, we not only master a basic skill but also develop a deeper understanding of the world around us. The ability to perform this seemingly simple calculation efficiently and accurately is a building block for success in various academic and professional pursuits. Mastering this fundamental skill allows for a smoother transition to more complex mathematical concepts and problem-solving scenarios. So, next time you encounter a seemingly basic multiplication problem, remember the hidden depths and the widespread relevance that lie beneath the surface.
Latest Posts
Latest Posts
-
Rabi Crops And Kharif Crops
Sep 23, 2025
-
What Are Factors Of 64
Sep 23, 2025
-
Describing Words Starting With V
Sep 23, 2025
-
Gandhi Peace Prize Jury Members
Sep 23, 2025
-
100 Cm Converted To Inches
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 6 5 X 2 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.