5 Square Root Of 3
seoindie
Sep 18, 2025 · 6 min read
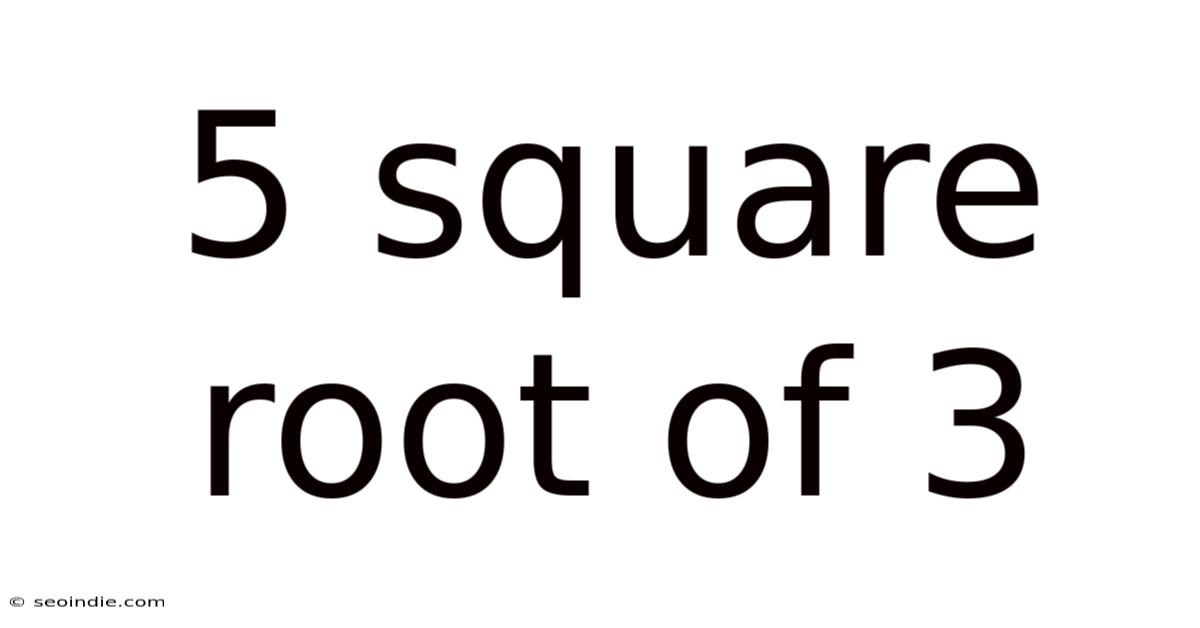
Table of Contents
Unveiling the Mysteries of 5√3: A Deep Dive into Irrational Numbers
The expression "5√3" might seem intimidating at first glance, conjuring images of complex mathematical equations and endless calculations. However, understanding this seemingly simple expression opens a door to a fascinating world of irrational numbers, their properties, and their applications in various fields. This article will serve as a comprehensive guide, exploring the meaning of 5√3, its numerical approximation, geometrical interpretations, and its relevance in advanced mathematical concepts. We'll delve into the intricacies of square roots, irrational numbers, and ultimately demystify this seemingly complex mathematical expression.
Understanding Square Roots and Irrational Numbers
Before we dissect 5√3, let's establish a firm foundation. The square root of a number (denoted by the symbol √) is a value that, when multiplied by itself, yields the original number. For example, √9 = 3 because 3 x 3 = 9. However, not all square roots result in whole numbers. This leads us to the concept of irrational numbers.
Irrational numbers are numbers that cannot be expressed as a simple fraction (a ratio of two integers). Their decimal representations are non-terminating and non-repeating, meaning they go on forever without ever settling into a repeating pattern. The most famous irrational number is π (pi), representing the ratio of a circle's circumference to its diameter. √3 is another example; its decimal representation begins 1.7320508... and continues indefinitely without repeating.
The expression 5√3 simply means 5 multiplied by the square root of 3. This combines the concept of multiplication with the concept of an irrational number.
Calculating and Approximating 5√3
While we cannot express 5√3 as a precise fraction, we can approximate its value using various methods. The most straightforward approach involves using a calculator:
-
Using a Calculator: Simply input 5 * √3 into a calculator. This will give you an approximate value, typically around 8.660254. The precision will depend on the calculator's capabilities.
-
Using a Square Root Table or Algorithm: Before the widespread availability of calculators, mathematicians relied on tables or algorithms (like the Babylonian method) to approximate square roots. These methods involve iterative calculations to refine the approximation to a desired level of accuracy.
-
Manual Approximation (less precise): We know that √3 is slightly greater than 1.7 (since 1.7² = 2.89 and 1.8² = 3.24). Therefore, a rough estimate of 5√3 could be obtained by multiplying 5 by 1.73 (a common approximation of √3), resulting in approximately 8.65. This method lacks accuracy but demonstrates the basic principle.
Geometrical Interpretation of 5√3
Beyond numerical calculations, 5√3 has a strong geometrical connection. Consider an equilateral triangle with side length x. The height (altitude) of this triangle is given by the formula (√3/2) * x. If we consider a triangle with a side length of 10 units, then the height would be (√3/2) * 10 = 5√3. Therefore, 5√3 represents the height of an equilateral triangle with a side length of 10 units.
Applications of 5√3 and Related Concepts
The concept of square roots and irrational numbers, including expressions like 5√3, are fundamental in many areas of mathematics and its applications:
-
Trigonometry: Irrational numbers frequently appear in trigonometric calculations. For example, the sine and cosine of certain angles involve square roots of irrational numbers.
-
Geometry: As demonstrated earlier, calculating areas, volumes, and distances in various geometrical shapes often involves square roots and irrational numbers. Consider the diagonal of a square with side length "a," which is given by a√2. Similar principles extend to more complex geometric figures.
-
Physics: Physical equations often involve irrational numbers. Calculations concerning projectile motion, wave phenomena, and oscillations may involve expressions similar to 5√3.
-
Engineering: In structural engineering and other fields, precise calculations involving irrational numbers are vital for creating stable and efficient designs.
-
Computer Graphics: Representing curves and shapes accurately in computer graphics often requires calculations involving irrational numbers.
-
Calculus: Irrational numbers are essential in calculus, particularly when working with limits, derivatives, and integrals. Many functions involve irrational components.
Advanced Mathematical Concepts Related to 5√3
The understanding of 5√3 can be expanded upon with more advanced mathematical concepts:
-
Complex Numbers: While 5√3 is a real number, the concept extends to complex numbers (numbers involving the imaginary unit i, where i² = -1). Complex numbers are crucial in various fields like electrical engineering and quantum mechanics.
-
Series and Limits: Irrational numbers like √3 can be expressed as infinite series or limits. These mathematical representations offer deeper insights into the nature of these numbers.
-
Continued Fractions: Irrational numbers can be expressed as continued fractions – an infinite expression of fractions within fractions. This representation offers an alternative way to approximate the value of irrational numbers.
Frequently Asked Questions (FAQ)
Q: Can 5√3 be simplified further?
A: No, 5√3 is already in its simplest form. The 5 is an integer, and √3 is an irrational number in its simplest radical form.
Q: What is the difference between 5√3 and √75?
A: While both involve the square root of 3, they are not identical. √75 can be simplified: √75 = √(25 * 3) = √25 * √3 = 5√3. Therefore, 5√3 and √75 are equivalent.
Q: How accurate does my approximation of 5√3 need to be?
A: The required accuracy depends on the context. For many practical applications, a few decimal places are sufficient. However, for highly precise calculations in fields like engineering or scientific research, more decimal places might be necessary.
Q: Are there any real-world examples where 5√3 is used?
A: While not explicitly stated as "5√3," the principles behind this expression are used extensively in engineering, physics, and other fields involving calculations with triangles and other geometrical shapes. The height of an equilateral triangle with a 10-unit side is a direct application. Calculations in architecture and surveying may implicitly involve similar irrational numbers.
Conclusion
The expression 5√3, although seemingly simple, serves as a gateway to understanding the fascinating world of irrational numbers and their significance in mathematics and its applications. From its geometrical interpretations to its relevance in advanced mathematical concepts, this expression underscores the power and beauty of mathematical principles. By grasping the fundamental concepts discussed in this article, readers can develop a stronger foundation in mathematics and appreciate the intricate connections between various mathematical concepts. The journey to mastering mathematics is ongoing, and the seemingly simple expression of 5√3 highlights the depth and richness of the subject. Continue exploring, questioning, and learning – the world of mathematics is full of exciting discoveries waiting to be unearthed!
Latest Posts
Latest Posts
-
1 1 3 Improper Fraction
Sep 18, 2025
-
Spanish Words Starting With A
Sep 18, 2025
-
Periodic Table Of Ionic Charges
Sep 18, 2025
-
Write In Terms Of I
Sep 18, 2025
-
Movement Along The Demand Curve
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 5 Square Root Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.