29 X 29 X 29
seoindie
Sep 24, 2025 · 5 min read
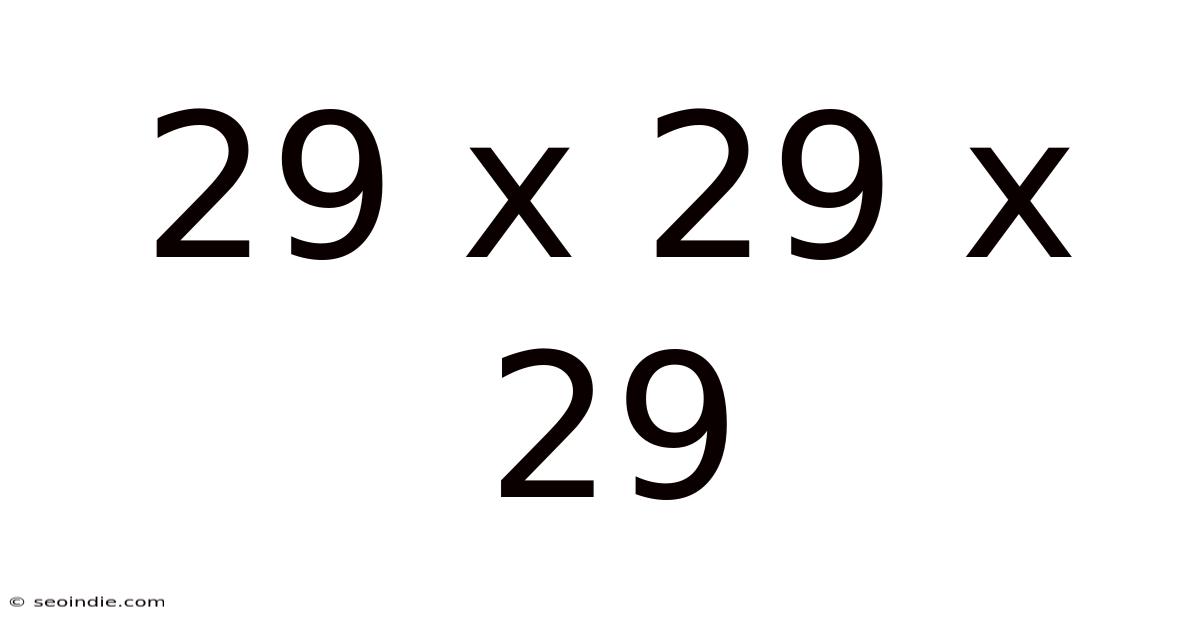
Table of Contents
Decoding the Curious Case of 29 x 29 x 29: A Deep Dive into Cubing, Calculation, and Conceptualization
The seemingly simple expression, 29 x 29 x 29, holds within it a surprising depth of exploration. At first glance, it appears to be a straightforward multiplication problem. However, delving into its solution opens doors to discussions about different calculation methods, the properties of cubes, and even the broader concept of mathematical exploration. This article will not just provide the answer but will guide you through several approaches to solving this problem, exploring the underlying mathematical principles, and considering its implications in various contexts.
Introduction: More Than Just a Number
The expression 29 x 29 x 29 represents the volume of a cube with sides measuring 29 units. Understanding this immediately provides context. While a calculator can quickly provide the numerical answer, the true educational value lies in the process of arriving at that answer and exploring the related concepts. This exploration extends beyond basic arithmetic into the realms of algebraic manipulation, estimation techniques, and even the visualization of three-dimensional space. This article serves as a comprehensive guide, catering to diverse learning styles and mathematical backgrounds.
Method 1: The Straightforward Approach – Manual Multiplication
The most fundamental approach involves performing the multiplication manually. This method reinforces basic multiplication skills and provides a step-by-step understanding of the calculation.
-
Step 1: 29 x 29: This can be broken down using the distributive property (FOIL method): (20 + 9) x (20 + 9) = 400 + 180 + 180 + 81 = 841.
-
Step 2: 841 x 29: Again, we can use the distributive property: (800 + 40 + 1) x 29 = 23200 + 1160 + 29 = 24389.
Therefore, 29 x 29 x 29 = 24389. This method, while time-consuming for larger numbers, strengthens fundamental mathematical understanding.
Method 2: Utilizing the Difference of Squares
A slightly more advanced technique employs the difference of squares identity (a² - b² = (a + b)(a - b)). While not directly applicable to 29 x 29 x 29 in its raw form, it can be used in conjunction with other methods to simplify calculations. For example, we could express 29 as (30 - 1), which could potentially simplify some steps within the multiplication. However, the benefit in this specific case is marginal compared to the added complexity.
Method 3: Leveraging a Calculator or Spreadsheet Software
In practical applications, using a calculator or spreadsheet software is the most efficient method for this calculation. These tools provide quick and accurate results, freeing up time for more complex mathematical analysis. This method is particularly useful when dealing with larger numbers or more intricate calculations.
Method 4: Estimation and Approximation
Before employing any precise calculation method, a quick estimate can provide a valuable sanity check. Rounding 29 to 30, we get 30 x 30 x 30 = 27000. This approximation shows that our final answer should be in the vicinity of 27000. This estimation technique enhances problem-solving skills and promotes a deeper understanding of numerical magnitudes. This is a powerful skill, especially when dealing with real-world applications where precise calculations might not always be necessary.
The Geometrical Interpretation: The 29 x 29 x 29 Cube
The result, 24389, represents more than just a numerical value. It represents the volume of a cube with sides of length 29 units. This visualization connects abstract mathematical concepts to tangible three-dimensional space. Imagine a cube made of small unit cubes; the total number of these unit cubes is 24389. This geometrical interpretation is crucial for applying this mathematical concept in fields like architecture, engineering, and physics.
Exploring Further: Extending the Concept
The principles behind calculating 29 x 29 x 29 extend to broader mathematical concepts:
-
Exponentiation: The expression can be written as 29³. This introduces the concept of exponentiation, a fundamental operation in algebra and calculus. Understanding exponentiation is crucial for comprehending exponential growth and decay, prevalent in various scientific and financial models.
-
Cubic Functions: The calculation is directly related to cubic functions, which are polynomials of degree three. Cubic functions have widespread applications in modeling various real-world phenomena, from the trajectory of projectiles to the growth of populations.
-
Higher Dimensions: While we’ve considered a three-dimensional cube, the concept can be extended to higher dimensions. Imagine a hypercube in four dimensions or even higher. These concepts are central to advanced mathematics and physics.
Frequently Asked Questions (FAQ)
-
What are the prime factors of 24389? The prime factorization of 24389 is 29³. This highlights the unique nature of this number as the cube of a prime number.
-
Are there any interesting mathematical properties associated with 24389? While 24389 isn't a particularly famous number in the realm of mathematical constants or special numbers, its connection to the cube of a prime number gives it a certain mathematical elegance.
-
Can this calculation be performed using different number bases? Yes, this calculation can be performed using different number bases, though the numerical representation of the result will vary. Converting the base 10 number to binary, hexadecimal, or other bases is a great way to reinforce understanding of different numerical systems.
-
What are some real-world applications of this type of calculation? Calculations involving cubes and volumes are essential in diverse fields like architecture (calculating the volume of buildings), engineering (determining the capacity of containers), and physics (calculating the volume of objects).
Conclusion: The Value of Exploration
The seemingly simple calculation of 29 x 29 x 29 provides a surprisingly rich educational experience. It’s not just about obtaining the answer (24389); it's about the journey of exploration. The different methods presented—manual multiplication, calculator use, estimation, and the geometrical interpretation—highlight diverse approaches to problem-solving. This journey further connects the calculation to broader mathematical concepts like exponentiation, cubic functions, and higher-dimensional geometry. By engaging with this problem, we not only enhance our mathematical skills but also develop a deeper appreciation for the elegance and interconnectedness of mathematics. The pursuit of understanding, even in seemingly simple calculations, unlocks a world of possibilities and strengthens our critical thinking abilities. The numerical answer is just the starting point; the real learning comes from the journey of exploration and the connections it unveils.
Latest Posts
Latest Posts
-
Square Root Of 1 9
Sep 24, 2025
-
What Numbers Multply Make 32
Sep 24, 2025
-
How To Pounds To Kilograms
Sep 24, 2025
-
How Big Is 36 In
Sep 24, 2025
-
Parts Of A Microscope Diagram
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 29 X 29 X 29 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.