2 Square Root Of 6
seoindie
Sep 12, 2025 · 5 min read
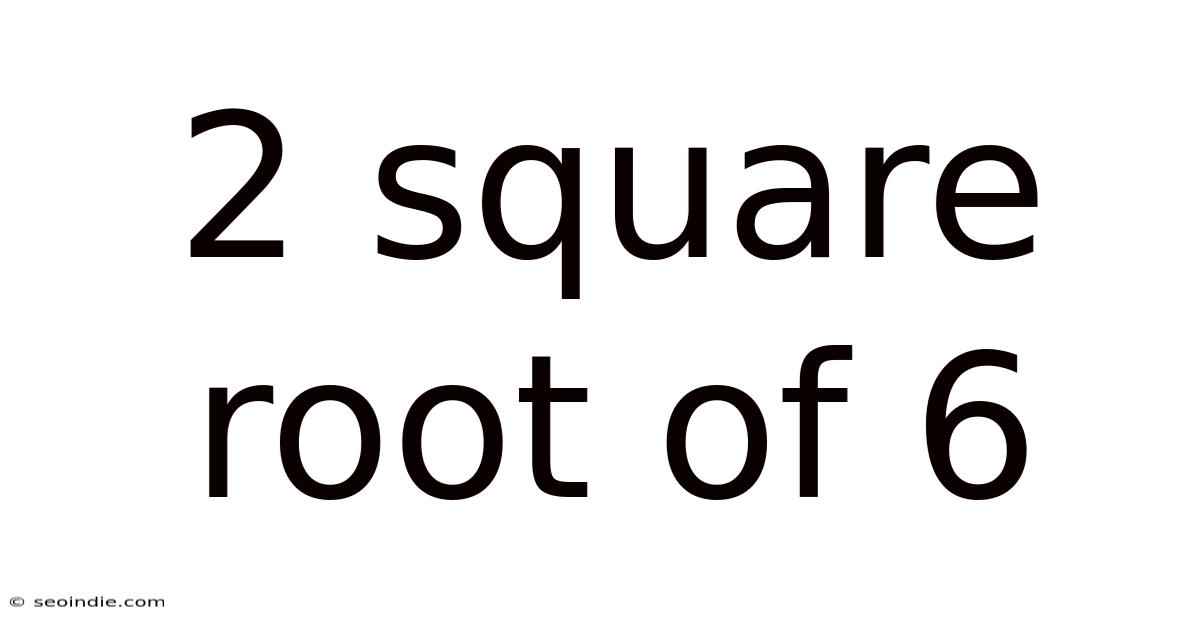
Table of Contents
Unveiling the Mysteries of 2√6: A Deep Dive into Irrational Numbers
Understanding the square root of a number is fundamental to mathematics. This article delves into the seemingly simple expression, 2√6, exploring its mathematical properties, practical applications, and the broader context of irrational numbers. We will dissect its components, explore methods for approximating its value, and delve into its significance within various mathematical fields. By the end, you'll have a much deeper appreciation for this seemingly simple number and its place in the larger mathematical landscape.
Understanding the Basics: What is 2√6?
At its core, 2√6 represents twice the square root of six. Let's break this down:
-
The Square Root (√): The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9.
-
The Number 6: Six is a composite number, meaning it's divisible by numbers other than 1 and itself (2 and 3).
-
The Multiplier 2: This simply means we're taking the square root of 6 and doubling the result.
Therefore, 2√6 is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation continues infinitely without repeating. This is a key characteristic that distinguishes it from rational numbers like 1/2 or 3/4.
Approximating the Value of 2√6
Since 2√6 is irrational, we can't express its exact value as a finite decimal. However, we can approximate it using various methods:
1. Using a Calculator: The simplest method is to use a calculator. Most calculators have a square root function (√). You would first calculate √6, then multiply the result by 2. This will give you a decimal approximation, which will vary in precision depending on your calculator's capabilities.
2. Using Estimation: We can estimate the value by recognizing that √6 lies between √4 (which is 2) and √9 (which is 3). Therefore, √6 is approximately 2.4. Multiplying this by 2 gives us an estimate of approximately 4.8.
3. Using the Babylonian Method (or Heron's Method): This iterative method provides increasingly accurate approximations of square roots. It involves starting with an initial guess, then refining the guess through repeated calculations. The formula is:
x_(n+1) = (x_n + S/x_n) / 2
Where:
x_nis the current guess.Sis the number whose square root is being calculated (in our case, 6).x_(n+1)is the improved guess.
Let's illustrate with an initial guess of 2.5:
x_1 = 2.5x_2 = (2.5 + 6/2.5) / 2 ≈ 2.45x_3 = (2.45 + 6/2.45) / 2 ≈ 2.449489796
We can continue this process to achieve higher levels of accuracy. Remember that this approximation is for √6; you would then need to multiply the result by 2 to get an approximation for 2√6.
The Significance of Irrational Numbers: Beyond 2√6
Irrational numbers, while seemingly abstract, hold immense significance in various areas of mathematics and beyond:
-
Geometry: Irrational numbers frequently appear in geometric calculations. The diagonal of a square with sides of length 1 is √2, an irrational number. The ratio of a circle's circumference to its diameter (π, or pi) is another famous irrational number.
-
Trigonometry: Trigonometric functions often produce irrational results. For example, sin(30°) = 1/2 (rational), but sin(15°) involves irrational numbers.
-
Calculus: Irrational numbers play a crucial role in calculus, particularly in the context of limits and integration.
-
Physics: Irrational numbers appear in numerous physical phenomena and equations, from the calculation of gravitational forces to the modeling of wave behavior.
2√6 in Practical Applications
While 2√6 might not be as prominently featured as π or e (Euler's number), it still has practical applications within mathematical contexts:
-
Solving Equations: It might appear as a solution to certain quadratic or higher-order equations.
-
Vector Calculations: In physics and engineering, vectors can have magnitudes involving irrational numbers like 2√6.
-
Geometric Problems: Specific geometric problems, involving areas or lengths, may lead to solutions involving 2√6.
Frequently Asked Questions (FAQ)
Q: Is 2√6 a rational or irrational number?
A: 2√6 is an irrational number. It cannot be expressed as a fraction of two integers.
Q: How can I simplify 2√6?
A: 2√6 is already in its simplest form. The number 6 has no perfect square factors other than 1, so the square root cannot be further simplified.
Q: What is the approximate decimal value of 2√6?
A: Using a calculator, the approximate value of 2√6 is about 4.89897948557. Remember, this is an approximation since the true value is irrational and extends infinitely.
Q: What is the difference between √6 and 2√6?
A: √6 represents the square root of 6, while 2√6 represents twice the square root of 6. The latter is simply double the value of the former.
Q: Are there other numbers similar to 2√6?
A: Yes, many other numbers share the characteristic of being irrational multiples of square roots. Examples include 3√2, 5√5, or even expressions like 2√(15). These all share the characteristic of infinite, non-repeating decimal representations.
Conclusion: Appreciating the Intricacies of Irrational Numbers
While the expression 2√6 might appear simple at first glance, it opens a window into the fascinating world of irrational numbers. Understanding its properties, methods for approximation, and its relevance within broader mathematical contexts provides a richer appreciation for the complexities and beauty of mathematics. Its existence highlights the limitations of representing all numbers as simple fractions and emphasizes the role of approximation in practical applications. The journey from a seemingly simple number to a deeper understanding of irrational numbers showcases the power of mathematical exploration and the interconnectedness of mathematical concepts. By exploring 2√6, we've touched upon fundamental concepts that underpin many areas of mathematics and science.
Latest Posts
Latest Posts
-
How Do You Spell 56
Sep 12, 2025
-
How Many Lbs In 6kg
Sep 12, 2025
-
90 Square Meters In Feet
Sep 12, 2025
-
How Many Metalloids Are There
Sep 12, 2025
-
The Square Root Of 8
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 2 Square Root Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.