10000 / 4 / 10
seoindie
Sep 19, 2025 · 5 min read
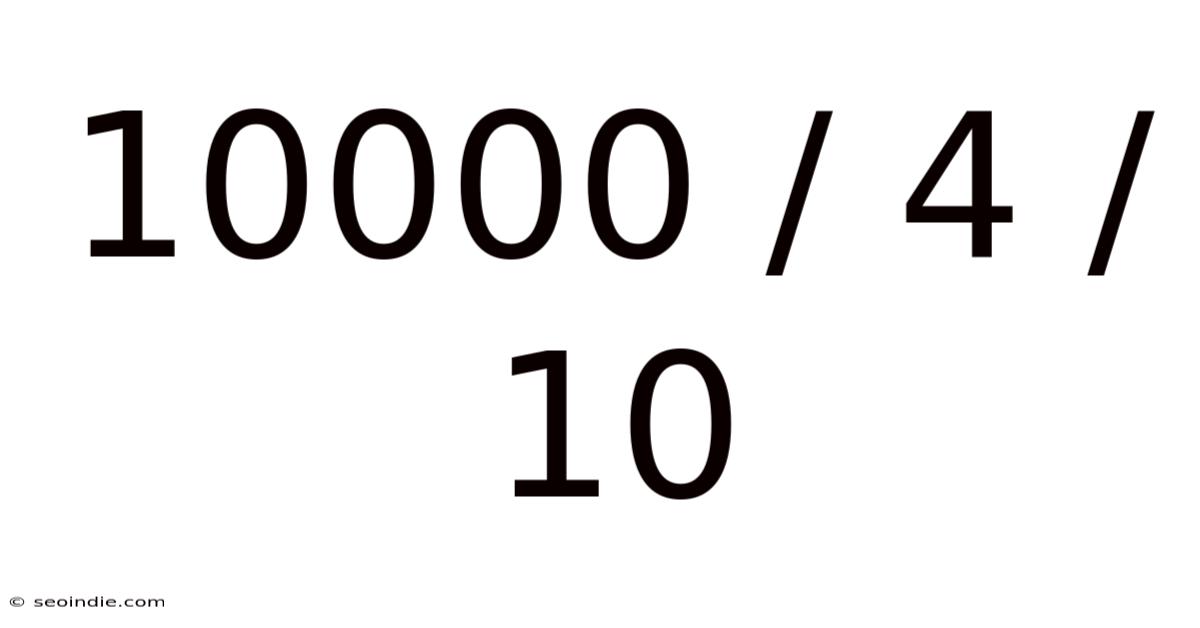
Table of Contents
Decoding 10000 / 4 / 10: A Deep Dive into Mathematical Operations and Problem-Solving
This article explores the seemingly simple mathematical expression "10000 / 4 / 10," delving beyond the immediate calculation to uncover the underlying principles of order of operations, the importance of parentheses, and the broader applications of these concepts. We'll dissect this expression step-by-step, explaining the process clearly and providing insightful examples to enhance understanding. This will be beneficial for students learning about basic arithmetic, as well as those wanting a refresher on order of operations. Understanding how to solve this seemingly simple problem lays the groundwork for more complex mathematical challenges.
Understanding Order of Operations (PEMDAS/BODMAS)
Before we tackle 10000 / 4 / 10, it's crucial to understand the order of operations. This is a set of rules that dictates the sequence in which mathematical operations should be performed to obtain the correct result. These rules are often remembered using acronyms like PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms represent the same fundamental concept.
-
Parentheses/Brackets: Calculations within parentheses or brackets are always performed first. This ensures that complex expressions are broken down into manageable parts.
-
Exponents/Orders: Exponents (powers or indices) are evaluated next. This includes operations like squaring, cubing, or raising a number to any power.
-
Multiplication and Division: These operations are performed from left to right. It's not multiplication first, then division. The order is determined by the sequence in which they appear in the expression.
-
Addition and Subtraction: Similar to multiplication and division, addition and subtraction are performed from left to right. The order is determined by their appearance in the expression.
Solving 10000 / 4 / 10
Now, let's apply the order of operations to solve 10000 / 4 / 10. Since there are no parentheses or exponents, we proceed directly to division.
Following the left-to-right rule, we first perform 10000 / 4:
10000 / 4 = 2500
Now, we take the result (2500) and perform the next division:
2500 / 10 = 250
Therefore, the solution to 10000 / 4 / 10 is 250.
The Importance of Parentheses
Let's consider what happens if we introduce parentheses to the expression. The placement of parentheses significantly alters the result. Consider these examples:
-
(10000 / 4) / 10: This expression is equivalent to the original problem, as the parentheses only reinforce the existing left-to-right order of operations. The result remains 250.
-
10000 / (4 / 10): This expression yields a different result. Following the order of operations, we perform the calculation inside the parentheses first:
4 / 10 = 0.4
Then, we perform the remaining division:
10000 / 0.4 = 25000
This example highlights the critical role of parentheses in specifying the order of operations and consequently, changing the final answer. The correct answer depends entirely on the intended grouping of the numbers and operations.
Real-World Applications
While this might seem like a simple mathematical problem, the principles involved have far-reaching applications in various fields:
-
Computer Programming: Order of operations is fundamental in programming. Programming languages follow strict rules of precedence, mirroring PEMDAS/BODMAS, to ensure that calculations are performed correctly. Incorrect order of operations can lead to program errors and unexpected results.
-
Engineering and Physics: Many engineering and physics calculations involve complex formulas that rely on the correct application of the order of operations. From calculating forces in structural engineering to determining trajectories in physics, adhering to these rules is essential for accurate results.
-
Finance and Accounting: Financial calculations, including compound interest, loan repayments, and investment returns, necessitate precise application of the order of operations. Errors can lead to significant financial implications.
-
Data Analysis: In data analysis and statistics, applying the correct order of operations is vital when performing calculations involving large datasets and complex formulas.
-
Everyday Life: Even in everyday scenarios, we subconsciously use the order of operations when dealing with quantities and calculations, for example, when dividing ingredients for a recipe or calculating the cost of several items.
Frequently Asked Questions (FAQ)
Q: What if I use a calculator to solve 10000 / 4 / 10? Will I get the same result?
A: Most standard calculators will follow the order of operations correctly, yielding the result of 250. However, it's always a good practice to understand the underlying mathematical principles, rather than relying solely on a calculator. Some older or simpler calculators might not handle the order of operations correctly, depending on how the expression is entered.
Q: Why is understanding order of operations important?
A: Understanding the order of operations is fundamental to performing accurate mathematical calculations. Without it, you risk obtaining incorrect results, which can have significant consequences in various fields, from simple everyday calculations to complex scientific computations.
Q: Are there any other ways to write the expression 10000 / 4 / 10 to make it clearer?
A: Using parentheses, as shown in the examples above, can clarify the intended order of operations. For instance, (10000/4)/10 eliminates any ambiguity. Fraction notation can also be used to represent the expression more clearly.
Q: What happens if I change the order of the numbers?
A: Changing the order of the numbers will significantly change the result. For example, 10/4/10000 will give a different answer than 10000/4/10. The order of operations dictates that calculations are performed sequentially from left to right.
Conclusion: Mastering Mathematical Fundamentals
The seemingly simple problem of 10000 / 4 / 10 serves as a valuable lesson in understanding the fundamental principles of mathematical operations. Mastering the order of operations (PEMDAS/BODMAS) is not just about getting the right answer; it's about understanding the logic and structure underlying all mathematical calculations. This understanding forms the bedrock for tackling more complex mathematical problems and is crucial in various fields requiring accurate numerical computations. By understanding these concepts, we are better equipped to solve complex problems, improve critical thinking skills and appreciate the beauty and precision of mathematics. Remember to always prioritize understanding the underlying principles and to use parentheses to clarify your calculations where necessary.
Latest Posts
Latest Posts
-
Words That End In The
Sep 19, 2025
-
What Is 23 Divisible By
Sep 19, 2025
-
Words With S C O
Sep 19, 2025
-
42 Sq Meters To Feet
Sep 19, 2025
-
How Far Is 7 Kilometers
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 10000 / 4 / 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.